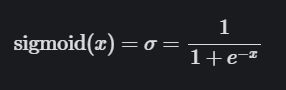《深度学习》之 前馈神经网络 原理 详解
前馈神经网络
1. 深度学习：
**定义：**深度学习是机器学习的一个研究方向，它基于一种特殊的学习机制。其特点是建立一个多层学习模型，深层级将浅层级的输出作为输入，将数据层层转化，使之越来越抽象。是模拟人脑接受外界刺激时处理信息和学习的方式。
应用领域：
- 语音识别系统
- 搜索模式
- 图像识别
- 自动驾驶
2.从感知机到多层网络
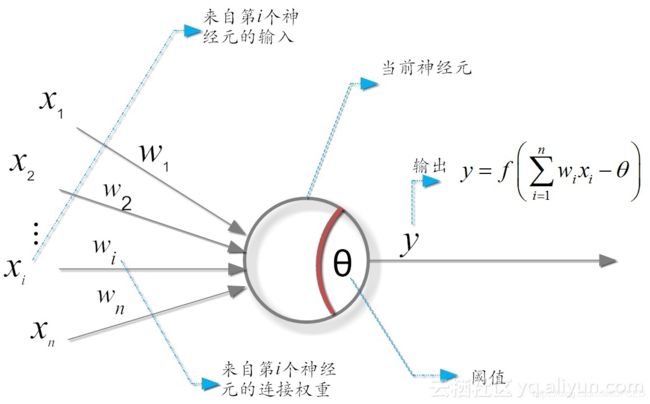
近代最常用的NN模型（神经网络模型）源于 1943年 McCulloch 和 Pitts 提出的 McCulloch-Pitts 神经元模型（简称M-P神经元模型），它针对单个神经元进行了数学建模。具体而言，M-P模型有如下三个功能：
- 能够接受n个输入信号
- 能够为输入信号分配权重
- 能够将得到的信号进行汇总，变换并输出
（图片来自网络）
其中 y 为 激活函数，θ为偏置量，即神经元对输入信号的平移
感知机的作用可以理解为对输入空间进行直线划分，单层感知机虽然可以解决与（AND）和或（OR）问题 ，却无法解决最简单的非线性可分问题---------异或问题
2.1多层前馈神经网络
每层神经元与下一层神经元全互联，神经元之间不存在同层连接，也不存在跨层连接，这样的结构被称为“多层前馈神经网络”。
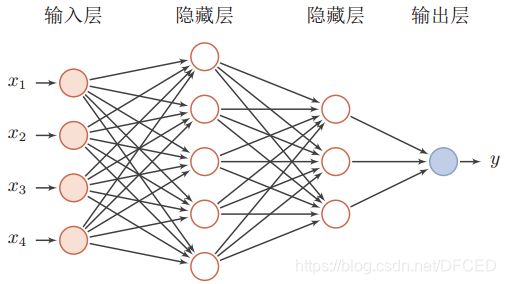
（图片来自网络）
神经网络的学习过程，是根据训练数据来调整神经元之间的权重以及每个功能神经元的阈值；总之，神经网络学到的东西，蕴含在权值和阈值中
注意：
- “前馈”并不指信号不能向后传，而是指网络拓扑结构上不存在环或回路
3.反向传播算法（简称 BP）
3.1 算法流程
其主要思想是：
（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；
（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；
（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。
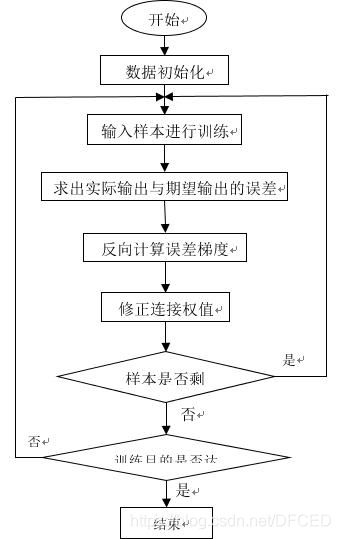
（图片来自网络）
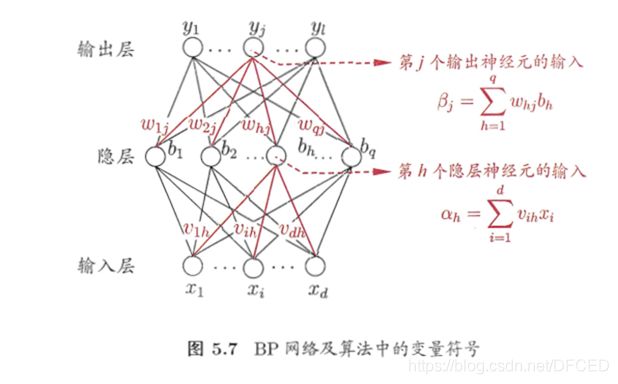
（图片来自网络）
BP算法基于梯度下降策略。以目标的负梯度方向对参数进行调整
4. 激活函数
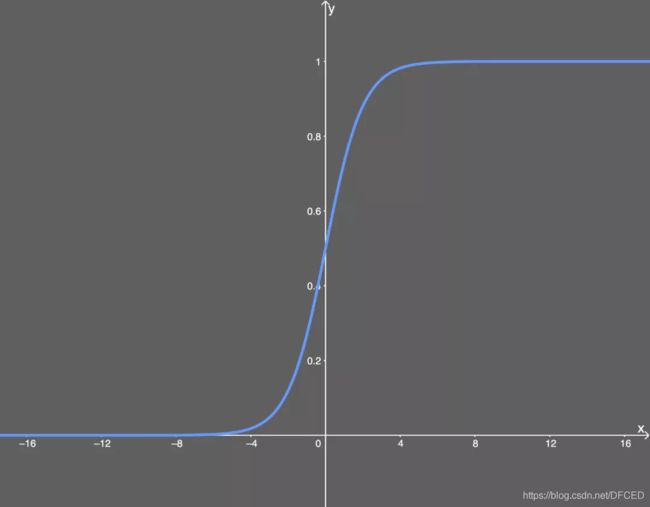
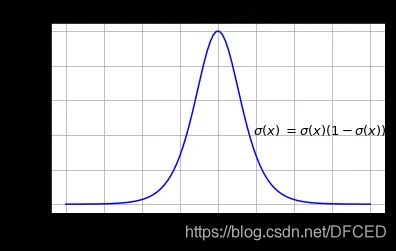
4.1 sigmoid 函数
- sigmoid函数： 是一个logistic函数，不管输入什么，输出值都在0到1之间。也就是说，你输入的每个神经元、节点或激活都会被缩放为一个介于 0 到 1 之间的值。
（图片来自网络）
（图片来自网络）
Sigmoid 导数
（图片来自网络）
Sigmoid 函数的三个主要缺陷：
1. 梯度消失：注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播。
2. 不以零为中心：Sigmoid 输出不以零为中心的。
3. 计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂。
4.2 Tanh 函数
（图片来自网络）
Tanh 导数
（图片来自网络）
Tanh 激活函数又叫作双曲正切激活函数（hyperbolic tangent activation function）。与 Sigmoid 函数类似，Tanh 函数也使用真值，但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同，Tanh 函数的输出以零为中心，因为区间在-1 到 1 之间。你可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值。
缺点：
- Tanh 函数也会有梯度消失的问题，因此在饱和时也会「杀死」梯度。
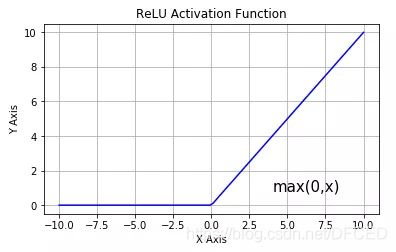
4.3 修正线性单元（ReLU）
（图片来自网络）
ReLu 导数
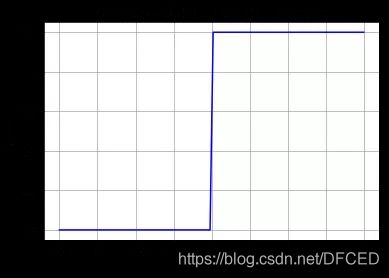
从上图可以看到，ReLU 是从底部开始半修正的一种函数。数学公式为：
当输入 x<0 时，输出为 0，当 x> 0 时，输出为 x。该激活函数使网络更快速地收敛。它不会饱和，即它可以对抗梯度消失问题，至少在正区域（x> 0 时）可以这样，因此神经元至少在一半区域中不会把所有零进行反向传播。由于使用了简单的阈值化（thresholding），ReLU 计算效率很高。
缺点
-
不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心。
-
前向传导（forward pass）过程中，如果 x < 0，则神经元保持非激活状态，且在后向传导（backward pass）中「杀死」梯度。这样权重无法得到更新，网络无法学习。当 x = 0 时，该点的梯度未定义，但是这个问题在实现中得到了解决，通过采用左侧或右侧的梯度的方式。
为了解决 ReLU 激活函数中的梯度消失问题，当 x < 0 时，我们使用 Leaky ReLU——该函数试图修复 dead ReLU 问题。下面我们就来详细了解 Leaky ReLU。
4.4 Leaky ReLU
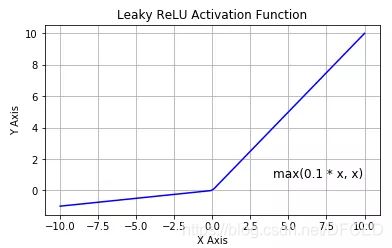
该函数试图缓解 dead ReLU 问题。数学公式为：
Leaky ReLU 的概念是：当 x < 0 时，它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题，但是使用该函数的结果并不连贯。尽管它具备 ReLU 激活函数的所有特征，如计算高效、快速收敛、在正区域内不会饱和。
Leaky ReLU 可以得到更多扩展。不让 x 乘常数项，而是让 x 乘超参数，这看起来比 Leaky ReLU 效果要好。该扩展就是 Parametric ReLU。
Leaky ReLU 可以得到更多扩展。不让 x 乘常数项，而是让 x 乘超参数，这看起来比 Leaky ReLU 效果要好。该扩展就是 Parametric ReLU。
4.5 Parametric ReLU
PReLU 函数的数学公式为：
其中是超参数。这里引入了一个随机的超参数，它可以被学习，因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度，有了这种能力，它们可以变成 ReLU 或 Leaky ReLU。
4.6 Swish
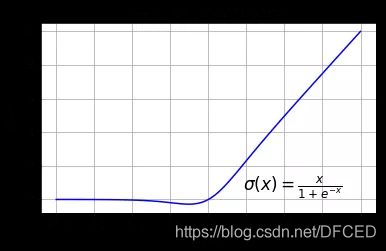
该函数又叫作自门控激活函数，它近期由谷歌的研究者发布，数学公式为：
Swish 激活函数的性能优于 ReLU 函数。
根据上图，我们可以观察到在 x 轴的负区域曲线的形状与 ReLU 激活函数不同，因此，Swish 激活函数的输出可能下降，即使在输入值增大的情况下。大多数激活函数是单调的，即输入值增大的情况下，输出值不可能下降。而 Swish 函数为 0 时具备单侧有界（one-sided boundedness）的特性，它是平滑、非单调的
参考：
《深度学习》 花书
复旦大学 《深度学习》