RepVGG：使VGG样式的ConvNets再次出色

目录

摘要

1、引言

2、为什么要用VGG模型？

2、相关工作

2.1、从单路径到多分支

2.2、有效地训练单路径模型

3、通过结构重参数构建RepVGG

3.1、简单即快速，节省内存，灵活

3.2、训练时的多分支体系结构

3.3、推理时的结构性重参数化

3.4、结构设计

4、实验

4.1、RepVGG用于ImageNet分类

4.3、语义分割

4.4、局限性

5、结论

6、ACNet

7、RepVGG的核心模块实现code

---

摘要

我们提出了一种简单而强大的卷积神经网络架构，该架构具有类似于VGG的推理时的模型结构，该推理模型仅由3*3卷积和ReLU的堆叠组成，而训练时模型具有多个分支拓扑结构。训练时和推理时架构的这种解耦是通过结构性重参数化(re-parameterization)”技术实现的，因此该模型称为RepVGG。在ImageNet数据集上，RepVGG取得了超过80%的top-1精度，这是plain模型首次达到如此高的精度。在NVIDIA 1080TiGPU上，RepVGG比ResNet50快83%，比ResNet101快101%，同时具有更高的精度；相比EfficientNet与RegNet，RepVGG表现出了更好的精度-速度均衡。可以在https://github.com/megvii-model/RepVGG找到代码和训练好的模型。 

该文的主要贡献包含以下三个方面：

1）提出了一种简单有强有的CNN架构RepVGG，相比EfficientNet、RegNet等架构，RepVGG具有更佳的精度-速度均衡；

2）提出采用重参数化技术对plain架构进行训练-推理解耦；

3）在图像分类、语义分割等任务上验证了RepVGG的有效性。

1、引言

    卷积神经网络（ConvNets）已成为许多任务的主流解决方案。 VGG [30]通过由conv，ReLU和pooling堆叠组成的简单体系结构，在图像识别方面取得了巨大成功。 有了Inception [32、33、31、17]，ResNet [10]和DenseNet [15]，许多研究兴趣都转移到了良好设计的体系结构上，从而使模型变得越来越复杂。 通过自动[43、28、22]或手动[27]架构搜索，或在基础架构上搜索的复合缩放策略，可以获得一些最近的强大架构[34]。

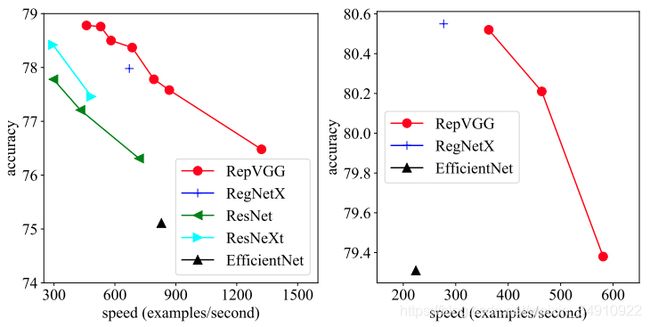
                                                                 图1：ImageNet上的Top-1准确性与实际速度的关系。左：轻量级和中量级。

RepVGG，以及在120个epoch内训练过的基线。右图：重量级模型经过200个epoch的训练。在相同的1080Ti上测试了速度，批次大小为128，全精度（fp32），单次裁剪，并以张/秒为单位进行了测量。 EfficientNet-B3 [34]的输入分辨率为300，其他分辨率的输入分辨率为224。

2、为什么要用VGG模型？

除了我们相信简单就是美以外，VGG式极简模型至少还有五大现实的优势（详见论文）。

1）3x3卷积非常快。在GPU上，3x3卷积的计算密度（理论运算量除以所用时间）可达1x1和5x5卷积的四倍。

2）单路架构非常快，因为并行度高。同样的计算量，“大而整”的运算效率远超“小而碎”的运算。

3）单路架构省内存。例如，ResNet的shortcut虽然不占计算量，却增加了一倍的显存占用。

4）单路架构灵活性更好，容易改变各层的宽度（如剪枝）。

5）RepVGG主体部分只有一种算子：3x3卷积接ReLU。在设计专用芯片时，给定芯片尺寸或造价，我们可以集成海量的3x3卷积-ReLU计算单元来达到很高的效率。别忘了，单路架构省内存的特性也可以帮我们少做存储单元。

尽管许多复杂的ConvNet都比简单的ConvNet提供更高的准确性，但缺点很明显：

  1）复杂的多分支设计，降低了推断，内存利用率；

  2）一些组件(如：dconv， channel shuffle)等增加了内存访问成本，并且缺乏各种设备的支持。所以现在新的模型虽然FLOP低了，但是推理速度，并没有提升。

简单的ConvNet具有这样三点优势：

Fast：相比VGG，现有的多分支架构理论上具有更低的Flops，但推理速度并未更快。比如VGG16的参数量为EfficientNetB3的8.4倍，但在1080Ti上推理速度反而快1.8倍。这就意味着前者的计算密度是后者的15倍。

Flops与推理速度的矛盾主要源自两个关键因素：

1) MAC(memory access cose),比如多分支结构的Add与Cat的计算很小，但MAC很高;

2)并行度，已有研究表明：并行度高的模型要比并行度低的模型推理速度更快。

Memory-economical：多分支结构是一种内存低效的架构，这是因为每个分支的结构都需要在Add/Concat之前保存，这会导致更大的峰值内存占用；而plain模型则具有更好的内存高效特征。

Flexible：多分支结构会限制CNN的灵活性，比如ResBlock会约束两个分支的tensor具有相同的形状；与此同时，多分支结构对于模型剪枝不够友好。

                                                                               图2：RepVGG架构示意图。

RepVGG有5个阶段，并在阶段开始时通过stride=2卷积进行下采样。在这里，我们仅显示特定阶段的前4层。受ResNet [10]的启发，我们也使用identity和1*1个分支，但仅用于训练。

普通模型要达到与多分支体系结构相当的性能水平，这是一个挑战。一种解释是，多分支拓扑，例如，ResNet，使模型成为许多较浅模型的隐式集合[35]，因此训练多分支模型可以避免梯度消失的问题。

由于多分支架构的好处全都在训练上，而缺点在推理上是不希望有的，我们建议通过结构重新参数化将训练时的多分支和推理时的普通架构分离，这意味着通过转换其参数将模型从一个结构转换为另一个结构。 具体而言，网络结构与一组参数耦合，例如，用四阶内核张量表示卷积层。 如果可以将某个结构的参数转换为由另一结构耦合的另一组参数，则可以用后者等效地替换前者，从而更改整个网络体系结构。

具体而言，我们使用identity和1*1的分支来构造训练时的RepVGG，这受ResNet的启发，但以不同的方式可以通过结构重新参数化除去分支（图2,4）。经过训练后，我们用简单的代数进行变换，因为一个等价分支可以看作是一个退化的1*1conv，而后者又可以看作是一个退化的3* 3 conv，因此我们可以用原始3 *3内核，identity和1*1分支以及批处理规范化（BN）[17]层的训练参数。因此，转换后的模型具有3*3 conv层的堆叠，将其保存以进行测试和部署。

值得注意的是，推理时RepVGG的主体仅涉及一种类型的操作：3*3 conv后跟ReLU，这使RepVGG在GPU等通用计算设备上快速运行。更好的是，RepVGG允许专用硬件实现更高的速度，因为给定芯片尺寸和功耗，我们需要的操作类型越少，我们可以集成到芯片上的计算单元就越多。即，专用于RepVGG的推理芯片可以具有大量的3*3-ReLU单元和更少的存储单元（因为普通拓扑在存储方面很经济，如图3所示）。我们的贡献总结如下。 1）我们提出了RepVGG，这是一种简单的体系结构，与最新技术相比，具有良好的速度精度折衷。  2）我们建议使用结构重新参数化将训练时的多分支拓扑与推理时的纯体系结构分离。 3）我们已经展示了RepVGG在图像分类和语义分割中的有效性，以及实现的效率和简便性。

2、相关工作

2.1、从单路径到多分支

    在VGG [30]将ImageNet分类的top-1准确性提高到70％以上之后，有很多创新使ConvNets复杂化以实现高性能，例如当代的GoogLeNet [32]和后来的Inception模型[33]。 [3] [31，17，17]采用精心设计的多分支体系结构，ResNet [10]提出了简化的两分支体系结构，而DenseNet [15]通过将低层和许多高层连接在一起使拓扑更加复杂。 神经架构搜索（NAS）[43、28、22、34]和手动设计空间设计[27]可以生成具有更高性能的ConvNet，但要付出大量计算资源或人力的代价。 NAS生成的模型的某些大型版本甚至无法在普通GPU上进行训练，因此限制了应用程序。 除了实现的不便外，复杂的模型可能会降低并行度[23]，从而减慢推理速度。

2.2、有效地训练单路径模型

已经尝试了无分支训练ConvNets。但是，先前的工作主要是试图使非常深的模型以合理的精度收敛，但是没有比复杂的模型获得更好的性能。因此，方法和结果模型既不简单也不实际。例如，提出了一种初始化方法[36]来训练极深的普通ConvNet。通过基于均场理论的方案，在MNIST上对10,000层网络进行了超过99％的训练精度，在CIFAR-10上进行了82％的训练精度。尽管这些模型不切实际（即使LeNet-5 [19]在MNIST上可以达到99.3％的准确度，而VGG-16在CIFAR-10上也可以达到93％以上的准确度），但是理论上的贡献是有见地的。最近的工作[24]结合了多种技术，包括Leaky ReLU，max-norm 和careful initialization。在ImageNet上，它显示具有147M参数的普通ConvNet可以达到74.6％的top-1精度，比其报告的基线（ResNet-101、76.6％，45M参数）低2％。

值得注意的是，本文不仅说明了简单模型可以很好地收敛，而且无意训练像ResNets这样的非常深的ConvNet。相反，我们旨在构建一个具有合理深度和有利的精度-速度折衷的简单模型，该模型可以通过最常见的组件（例如常规conv和BN）和简单的代数简单地实现。

3、通过结构重参数构建RepVGG

3.1、简单即快速，节省内存，灵活

至少有三个原因可以使用简单的Con-vNet：它们快速，节省内存和灵活。

快速：许多最新的多分支体系结构的理论FLOP低于VGG，但运行速度可能不快。 例如，VGG-16的FLOP是EfficientNet-B3的8.4倍[34]，但在1080Ti上的运行速度是1.8倍（表4），这意味着前者的计算密度是后者的15倍。 除了Winograd conv带来的加速之外，FLOP和速度之间的差异可以归因于两个重要因素，这些因素对速度有很大影响，但FLOP并未考虑这些因素：内存访问成本（MAC）和并行度 [23]。例如，尽管所需的分支加法或级联计算可以忽略不计，但MAC还是很重要的。此外，MAC在成组卷积中占时间使用的很大一部分。另一方面，在相同的FLOP下，具有高并行度的模型可能比具有低并行度的模型快得多。由于在Inception和自动生成的体系结构中广泛采用了多分支拓扑，因此使用了多个小运算符，而不是几个大运算符。先前的一项工作[23]报告说，NASNET-A [42]中的碎片运算符的数量（即，一个构建块中的单个转换或池化操作的数量）为13，这对具有强大并行计算能力的设备不友好例如GPU，并引入了额外的开销，例如内核启动和同步。相反，在ResNets中，此数字是2或3，我们将其设置为1：单个转换。

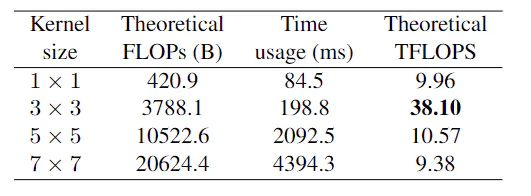
                         表1：在NVIDIA 1080Ti上，不同内核大小和批处理大小= 32，输入通道=输出通道= 2048，分辨率= 5656，步幅= 1时的速度测试。硬件预热后，平均使用时间为10次。

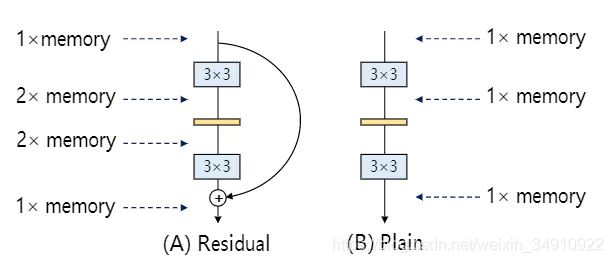
节省内存：多分支拓扑的内存效率低下，因为需要保留每个分支的结果，直到添加或串联为止，从而显着提高了内存占用的峰值。例如，如图3所示，需要保持输入到剩余块的时间，直到相加为止。如图3所示。假设该块保持特征图的大小，则作为输入的存储器占用的峰值为2。相反，简单的拓扑允许在操作完成后立即释放特定层的输入所占用的内存。在设计专用硬件时，普通的ConvNet可以进行深度内存优化并降低内存单元的成本，以便我们可以将更多计算单元集成到芯片上。

灵活：多分支拓扑对体系结构规范施加了约束。 例如，ResNet要求将conv层组织为残差块，这限制了灵活性，因为每个残差块的最后一个conv层必须产生相同形状的张量，否则快捷方式的添加就没有意义了。 更糟糕的是，多分支拓扑限制了通道修剪的应用[20，12]，这是删除一些不重要通道的实用技术，某些方法可以通过自动发现每层的适当宽度来优化模型结构[ 7]。 但是，多分支模型使修剪变得棘手，并导致明显的性能下降或低加速比[6、20、8]。 相反，简单的体系结构使我们可以根据我们的要求自由配置每个conv层，并进行修剪以获得更好的性能效率折衷。

                     图3：残差和普通模型中的峰值内存占用。如果残差块保持要素图的大小，则要素图占用的内存峰值将作为输入。与因此忽略的特征相比，模型参数占用的内存较小。

3.2、训练时的多分支体系结构

3.3、推理时的结构性重参数化

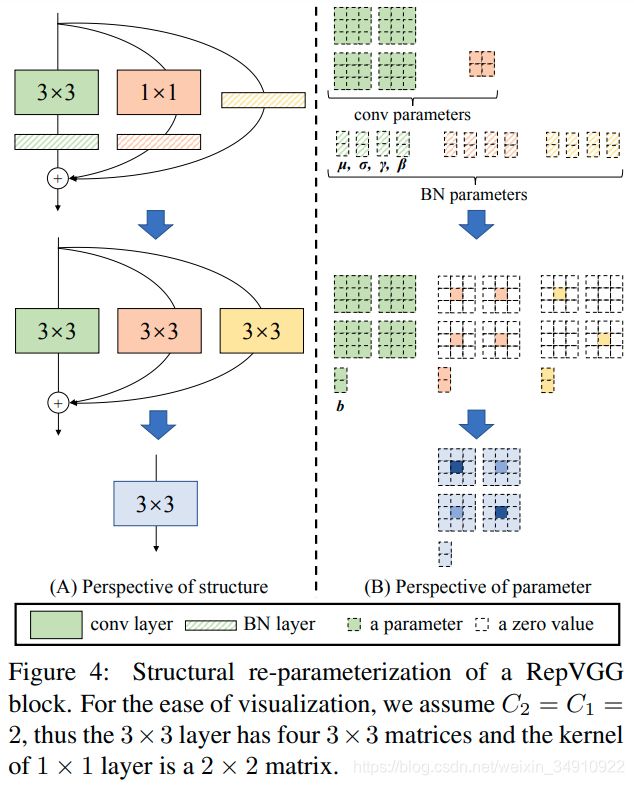
接下来，我们将介绍如何将已训练模块转换成单一的3*3 conv卷积用于推理。注意，在添加之前，我们在每个分支中都使用了BN下图给出了参数转换示意图。

3.4、结构设计

我们遵循三个简单的准则来决定每个阶段的层数。

第一个阶段具有更大的分辨率，故而更为耗时，为降低推理延迟仅仅采用了一个卷积层；最后一个阶段因为具有更多的通道，为节省参数量，故而仅设计一个卷积层；在倒数第二个阶段，类似ResNet，RepVGG放置了更多的层。

基于上述考量，RepVGG-A不同阶段的层数分别为1-2-4-14-1;与此同时，作者还构建了一个更深的RepVGG-B，其层数配置为1-4-6-16-1。RepVGG-A用于与轻量型网络和中等计算量网络对标，而RepVGG-B用于与高性能网络对标。

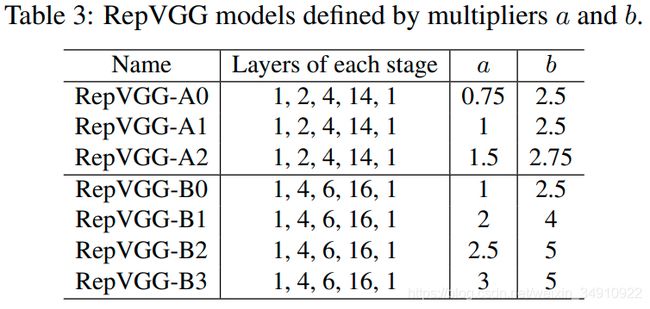
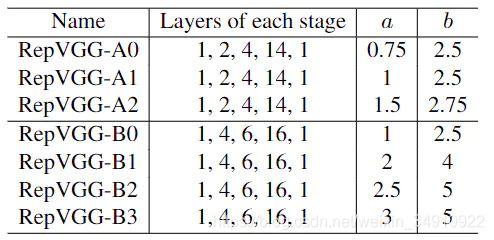
在不同阶段的通道数方面，作者采用了经典的配置64-128-256-512。与此同时，作者采用因子a控制前四个阶段的通道，因子b控制最后一个阶段的通道，通常b>a（我们期望最后一层具有更丰富的特征）。为避免大尺寸特征的高计算量，对于第一阶段的输出通道做了约束min(64, 64a)。基于此得到的不同RepVGG见下表。

为进一步降低计算量与参数量，作者还设计了可选的3*3组卷积替换标准卷积。具体地说，在RepVGG-A的3-5-7-...-21卷积层采用了组卷积；此外，在RepVGG-B的23-25-27卷积层同样采用了组卷积。

4、实验

在本节中，我们将RepVGG的性能与ImageNet上的基线进行比较，通过一系列的消融研究和比较证明结构重新参数化的重要性，并验证RepVGG在语义分割上的泛化性能[41]。

4.1、RepVGG用于ImageNet分类

我们首先将RepVGG与最常用的基准ResNets [10]进行比较。 为了与ResNet-18进行比较，我们将a设置为0:75； 对于RepVGG-A0，b = 2.5。 对于ResNet-34，我们使用更宽的RepVGG-A1。 为了使RepVGG的参数比ResNet-50略少，我们构建RepVGG-A2，其中a = 1.5； b = 2.75。 为了与更大的模型进行比较，我们构造了宽度增加的更深的RepVGG-B0 / B1 / B2 / B3。 对于那些具有交错的分组层的RepVGG模型，我们将g2 / g4附加到模型名称作为后缀。

                                                                                 表3：由乘数a和b定义的RepVGG模型。

为了训练轻量级和中量级模型，我们仅使用简单的数据增强管道，包括随机裁剪和左右翻转，遵循官方PyTorch示例[26]。我们在8个GPU上使用256的全局批处理大小，学习速率初始化为0.1，cosine annealing120个epochs，标准SGD的动量系数为0.9，权重衰减为，在conv和完全连接层的内核上。对于包括RegNetX-12GF，EfficientNet-B3和RepVGG-B3在内的重量级模型，我们使用5阶段预热，cosine annealing200epochs，标签平滑[33]和混合[39]（以下[11] ]），以及Autoaugment [4]（随机裁剪和翻转）的数据增强管道。 RepVGG-B2及其g2 / g4变体在两种设置中都经过培训。我们先在1080Ti GPU 上以128个批次的大小测试每个模型的速度，方法是先送入50个批次以预热硬件，然后再记录50个批次并记录使用时间。

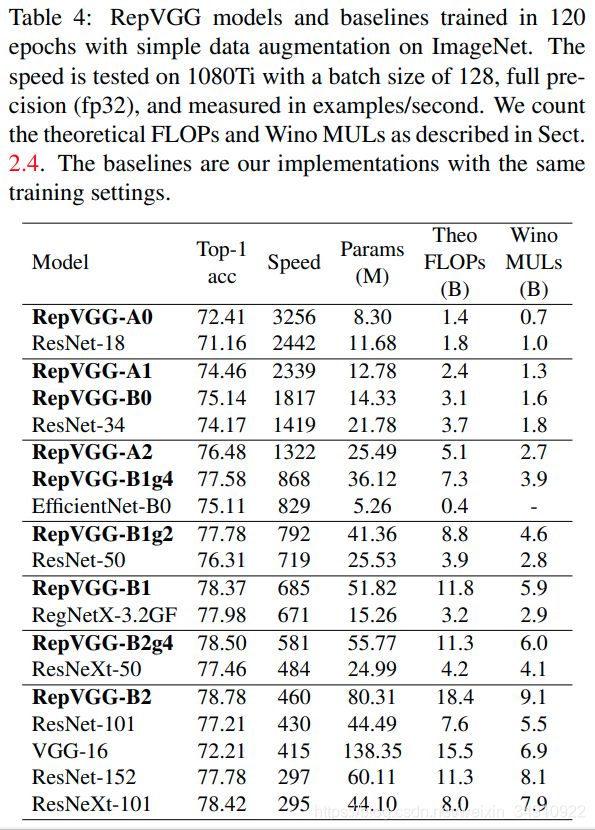
上表给出了RepVGG与不同计算量的ResNe及其变种在精度、速度、参数量等方面的对比。可以看到：RepVGG表现出了更好的精度-速度均衡，比如：

RepVGG-A0比ResNet18精度高1.25%，推理速度快33%；

RepVGG-A1比Resnet34精度高0.29%，推理速度快64%；

RepVGG-A2比ResNet50精度高0.17%，推理速度快83%；

RepVGG-B1g4比ResNet101精度高0.37%，推理速度快101%；

RepVGG-B1g2比ResNet152精度相当，推理速度快2.66倍。

另外需要注意的是：RepVGG同样是一种参数高效的方案。比如：相比VGG16，RepVGG-B2b168.com仅需58%参数量，推理快10%，精度高6.57%。

与此同时，还与EfficientNet、RegNet等进行了对比，对比如下：

RepVGG-A2比EfficientNet-B0精度高1.37%，推理速度快59%；

RepVGG-B1比RegNetX-3.2GF精度高0.39%，推理速度稍快；

此外需要注意：RepVGG仅需200epoch即可取得超过80%的top1精度，见上表对比。这应该是plain模型首次在精度上达到SOTA指标。相比RegNetX-12GF，RepVGG-B3的推理速度快31%，同时具有相当的精度。

尽管RepVGG是一种简单而强有力的ConvNet架构，它在GPU端具有更快的推理速度、更少的参数量和理论FLOPS；但是在低功耗的端侧，MobileNet、ShuffleNet会更受关注。

4.3、语义分割

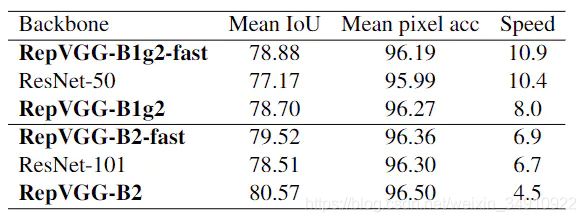
以RepVGG为主干网络，后面接PSPNet分割header。结果表明，RepVGG的骨架在平均IoU上具有更高的速度，分别比ResNet-50和ResNet-101优越1.71％和1.01％。令人印象深刻的是，RepVGG-B1g2-fast在mIoU方面优于ResNet-101主干网0.37，运行速度快62％。有趣的是，对于较大的模型，扩张似乎更有效，因为与RepVGG-B1g2-fast相比，使用更多扩张的conv层不会提高性能，但会以合理的速度将RepVGG-B2的mIuU提高1.05％。

                                                                         表7：以120个时期训练的RepVGG-B0与变体和基线的比较。

                       表8：在验证子集上测试的Cityscapes [3]上的语义分割。在同一1080Ti GPU上以批处理大小16，全精度（fp32）和输入分辨率713713测试了速度（示例/秒）。

4.4、局限性

RepVGG模型是快速，简单和实用的ConvNet，旨在在GPU和专用硬件上以最高速度运行，而无需考虑参数或理论FLOP的数量。尽管RepVGG模型的参数效率比ResNets高，但它们可能不如MobileNets [14、29、13]和ShuffleNets [40、23]等移动系统模型适合低功耗设备。

5、结论

我们提出了RepVGG，这是一个简单的体系结构，具有3*3 conv和ReLU的堆栈，这使其特别适用于GPU和专用推理芯片。通过我们的结构重新参数化方法，这样一个简单的Con-vNet在ImageNet上达到了80％的top-1精度，并且与最新的复杂模型相比，显示了良好的速度精度折衷。

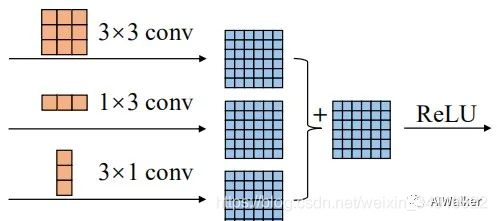
6、ACNet

从某种程度上讲，RepVGG应该是ACNet的的一种极致精简，比如上图给出了ACNet的结构示意图，它采用了三种卷积设计；而RepVGG则是仅仅采用了三个分支设计。ACNet与RepVGG的另外一点区别在于：ACNet是将上述模块用于替换ResBlock或者Inception中的卷积，而RepVGG则是采用所设计的模块用于替换VGG中的卷积。

https://my.oschina.net/u/4274857/blog/4512852

7、RepVGG的核心模块实现code

# code from https://github.com/DingXiaoH/RepVGG
class RepVGGBlock(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size,
                 stride=1, padding=0, dilation=1, groups=1, padding_mode='zeros', deploy=False):
        super(RepVGGBlock, self).__init__()
        self.deploy = deploy
        self.groups = groups
        self.in_channels = in_channels

        assert kernel_size == 3
        assert padding == 1

        padding_11 = padding - kernel_size // 2

        self.nonlinearity = nn.ReLU()

        if deploy:
            self.rbr_reparam = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size,
                                         stride=stride,
                                         padding=padding, dilation=dilation, groups=groups, bias=True,
                                         padding_mode=padding_mode)

        else:
            self.rbr_identity = nn.BatchNorm2d(
                num_features=in_channels) if out_channels == in_channels and stride == 1 else None
            self.rbr_dense = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size,
                                     stride=stride, padding=padding, groups=groups)
            self.rbr_1x1 = conv_bn(in_channels=in_channels, out_channels=out_channels, kernel_size=1, stride=stride,
                                   padding=padding_11, groups=groups)
            print('RepVGG Block, identity = ', self.rbr_identity)

    def forward(self, inputs):
        if hasattr(self, 'rbr_reparam'):
            return self.nonlinearity(self.rbr_reparam(inputs))

        if self.rbr_identity is None:
            id_out = 0
        else:
            id_out = self.rbr_identity(inputs)

        return self.nonlinearity(self.rbr_dense(inputs) + self.rbr_1x1(inputs) + id_out)

    def _fuse_bn(self, branch):
        if branch is None:
            return 0, 0
        if isinstance(branch, nn.Sequential):
            kernel = branch.conv.weight.detach().cpu().numpy()
            running_mean = branch.bn.running_mean.cpu().numpy()
            running_var = branch.bn.running_var.cpu().numpy()
            gamma = branch.bn.weight.detach().cpu().numpy()
            beta = branch.bn.bias.detach().cpu().numpy()
            eps = branch.bn.eps
        else:
            assert isinstance(branch, nn.BatchNorm2d)
            kernel = np.zeros((self.in_channels, self.in_channels, 3, 3))
            for i in range(self.in_channels):
                kernel[i, i, 1, 1] = 1
            running_mean = branch.running_mean.cpu().numpy()
            running_var = branch.running_var.cpu().numpy()
            gamma = branch.weight.detach().cpu().numpy()
            beta = branch.bias.detach().cpu().numpy()
            eps = branch.eps
        std = np.sqrt(running_var + eps)
        t = gamma / std
        t = np.reshape(t, (-1, 1, 1, 1))
        t = np.tile(t, (1, kernel.shape[1], kernel.shape[2], kernel.shape[3]))
        return kernel * t, beta - running_mean * gamma / std

    def _pad_1x1_to_3x3(self, kernel1x1):
        if kernel1x1 is None:
            return 0

        kernel = np.zeros((kernel1x1.shape[0], kernel1x1.shape[1], 3, 3))
        kernel[:, :, 1:2, 1:2] = kernel1x1
        return kernel

    def repvgg_convert(self):
        kernel3x3, bias3x3 = self._fuse_bn(self.rbr_dense)
        kernel1x1, bias1x1 = self._fuse_bn(self.rbr_1x1)
        kernelid, biasid = self._fuse_bn(self.rbr_identity)
        return kernel3x3 + self._pad_1x1_to_3x3(kernel1x1) + kernelid, bias3x3 + bias1x1 + biasid