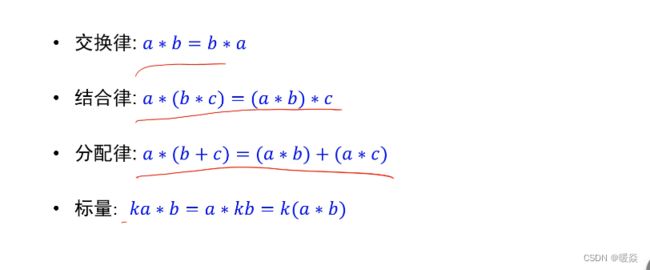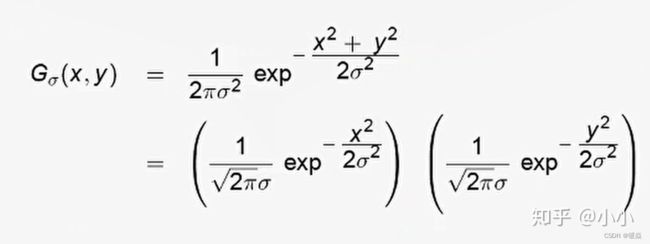【计算机视觉】计算机视觉与深度学习-04-图像去噪&卷积&边缘提取-北邮鲁鹏老师课程笔记
计算机视觉与深度学习-04-图像去噪&卷积-北邮鲁鹏老师课程笔记
- 图像噪声
-
- 噪声分类及产生原因
-
- 脉冲噪声&椒盐噪声
-
- 中值滤波器
-
- 中值滤波 vs 均值滤波
- 高斯噪声(Gaussian noise)
- 瑞利噪声
- 伽马噪声
- 指数噪声
- 均值噪声
- 图像去噪算法
-
- 空间滤波
- 变换域滤波
- 偏微分滤波
- 变分法
- 形态学噪声滤除器
- 卷积(convolution)
-
- 平均卷积噪声处理
- 卷积定义
- 卷积性质
-
- 卷积(convolution)与相关(correlation)
- 卷积与相关的转换
- 边界填充
-
- 为什么必须边界填充?
- 边界填充方法
-
- 常数填充
-
- 零填充(zero padding)
- 拉伸
- 镜像
- 卷积实例
-
- 单位脉冲核
- 锐化
- 平均卷积核
- 高斯卷积核
-
- 平均卷积核存在的问题
- 高斯卷积核定义
- 高斯卷积核生成步骤
-
- 确定卷积核的尺寸
- 设置高斯函数的标准差
- 计算卷积核各个位置权重值
- 对权重值进行归一化
- 高斯卷积核参数
-
- 卷积核尺寸大小(窗口大小)
- 高斯函数标准差σ
- 高斯卷积核参数经验法则
-
- 为什么高斯卷积核窗口大小是2*3*σ+1?
- 高斯核注意事项
-
- 高斯卷积非线性
- 高斯核权值非负
- 高斯核权值总和为1
- 高斯卷积核作用
-
- 低通滤波器
- 抑制噪声
- 实现图像平滑
- 高斯卷积核分解
-
- 大方差卷积分解为多个连续小方差卷积(计算结果不一定相等)
- 二维分解为两个一维(计算结果一定相等)
- 高斯卷积核分解的作用(降低算法复杂度)
- 边缘提取
-
- 边缘
- 为什么研究边缘?
- 边缘种类
-
- 表面法向不连续
- 深度不连续
- 表面颜色不连续
- 光照不连续
- 边缘检测
-
- 图像偏导
-
- 图像梯度的模
- 噪声的影响
-
- 噪声影响带来的问题
-
- 解决办法(先平滑处理)
- 高斯一阶偏导核
-
- 高斯一阶偏导卷积核的方差参数
- 高斯一阶偏导核注意事项
-
- 高斯的导数
- 卷积核中权值可为负
- 权值总和为0
- 高对比度点的响应值大
- 边缘检测目标
-
- Canny边缘检测器
-
- 高斯一阶偏导核卷积图像
- 计算每个点的梯度幅值和方向
- 非极大值抑制
- 门限过滤
-
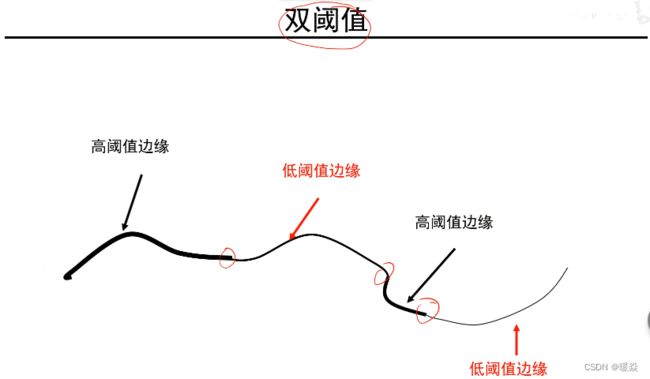
- 双阈值
图像噪声
噪声点,其实在视觉上看上去让人感觉很难受,直观理解就是它跟周围的像素点差异比较大,显得比较突兀,视觉看起来很不舒服,这就是噪声点。
参考:图像噪声 – csz795
噪声分类及产生原因
脉冲噪声&椒盐噪声

高斯卷积核(低通滤波器)并不能去除椒盐噪声和脉冲噪声。需要使用中值滤波器。
中值滤波器
中值滤波器是非线性操作。
刚开始的卷积核没有权重,当图像处理时,将9*9的卷积核套在图像的9个像素上,取这9个图像向上的像素值,排序求出其中值,并用该中值替换当前中心点像素值。
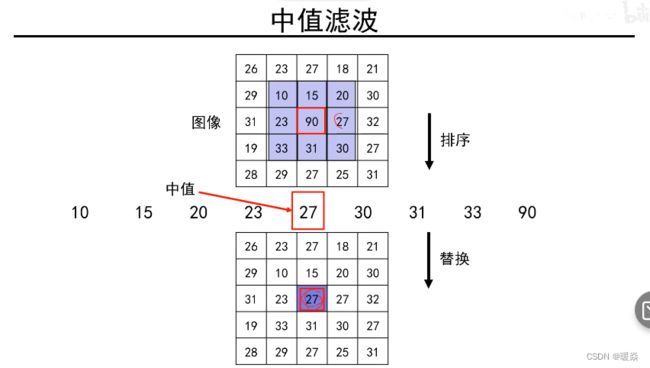
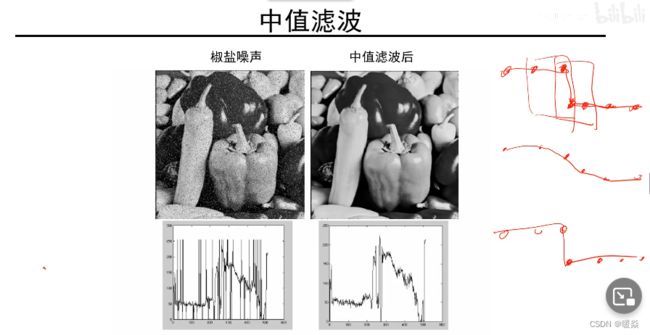
中值滤波 vs 均值滤波
中值滤波:卷积结果的像素值是图像原本就有这个像素值。
均值滤波:卷积结果的像素值是加权平均计算出的,可能原本并没有这个像素值。
高斯噪声(Gaussian noise)
高斯噪声(Gaussian noise)是指它的概率密度函数服从高斯分布的一类噪声。
高斯噪声数学模型是一个独立的加和模型 f ( x , y ) = f ^ ( x , y ) + η ( x , y ) f(x,y)=\hat{f}(x,y)+\eta (x,y) f(x,y)=f^(x,y)+η(x,y),一般认为 η ( x , y ) ∼ N ( μ , σ ) \eta(x,y) \sim N(\mu,\sigma) η(x,y)∼N(μ,σ),通常 μ = 0 , σ \mu=0,\sigma μ=0,σ很小。
即认为图像是由真实图像+高斯噪声组成的,高斯噪声的产生一个是由于采集器附加的噪声,另一个是由于光学问题带来的噪声。将两者合起来就是最终看到的带有噪声的图像。
因此对于高斯噪声就有了这样的假设:首先噪声的产生是相互独立的,而且服从均值为0的正态分布。


噪声的方差越大,高斯卷积核的方差或尺寸就要越大。
虽然高斯卷积核可以去除高斯噪声,但是更模糊(最下图比最上图模糊),坏的噪声去掉了,好的像素也受到了影响。
瑞利噪声
伽马噪声
指数噪声
均值噪声
图像去噪算法
空间滤波
空域滤波是在原图像上直接进行数据运行,对像素值进行处理。如邻域平均法、中值滤波、低通滤波等。
变换域滤波
图像变换域滤波是对图像进行某种变换,将图像从空间域转换到变换域,再对变换域中的变换系数进行处理,之后再从变换域转换到空间域,达到降噪目的。如傅里叶变换、余弦变换、小波变换等。
偏微分滤波
偏微分方程主要针对底层图像处理,它具有各向异性的特点,应用在图像降噪中,可以在降噪的同时很好地保持边缘信息。主要适用于低噪声密度图像,在处理高噪声密度图像时效果并不理想。
变分法
变分法降噪首先确定图像的能量函数,通过对能量函数的最小化工作,使图像达到平滑效果。此方法降噪的关键是找到合适的能量方程,保证演化的稳定性,获得理想效果。
形态学噪声滤除器
结合图像开闭操作进行降噪,先对图像进行开运算,然后再进行闭运算,将图像上的噪声去掉。此方法适用于图像中的对象尺寸比较大,且没有细节的图像。
卷积(convolution)
平均卷积噪声处理
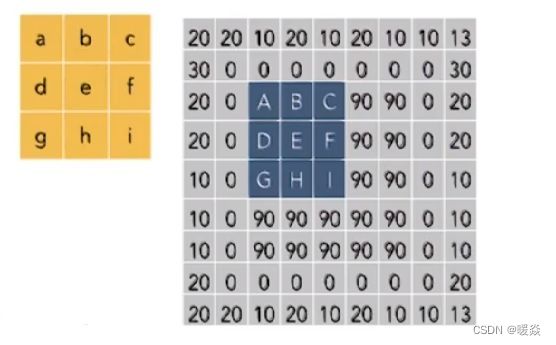
灰度图,像素值用一个[0,255]的数字表示,9*9的矩阵表示周围像素值。
下图中253明显比周围像素值大,是噪声。

一般将权值记录在卷积核中。

卷积定义
卷积性质
卷积(convolution)与相关(correlation)
相关运算,反应已有事物的内在关联,描述两个事物之间的相似性(包括自相关与互相关),并不是事物之间的相互影响。

相关可以看作是向量内积的推广(内积为两向量点乘,其物理意义为将一个向量投影到另一个向量)。内积越大,投影越大,两个向量间夹角越小,方向越一致,相似度越高。特别地,当内积为0时,两个向量是垂直的;只有当两个向量夹角为0时,内积最大(相关系数也最大)。因此,相关可反映两个向量空间的夹角。
注意相关不具有交换性。
卷积运算,反映事物的相互作用,并且这种相互作用受制于同一个影响因子。

卷积核在计算时需要旋转180度,但实际情况中,一般卷积核都是对称的,一般不需要旋转。
卷积与相关的转换
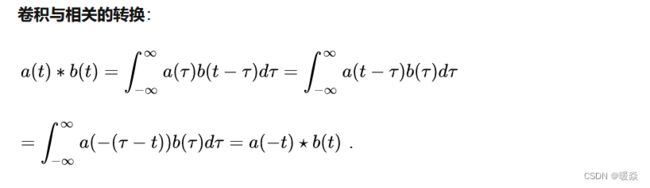
参考:卷积(convolution)与相关(correlation) – Hsuty
参考:卷积(convolution)与互相关(cross-correlation)的一点探讨 – 无迹
参考:卷积运算和相关运算的区别与物理含义? – Allen
边界填充
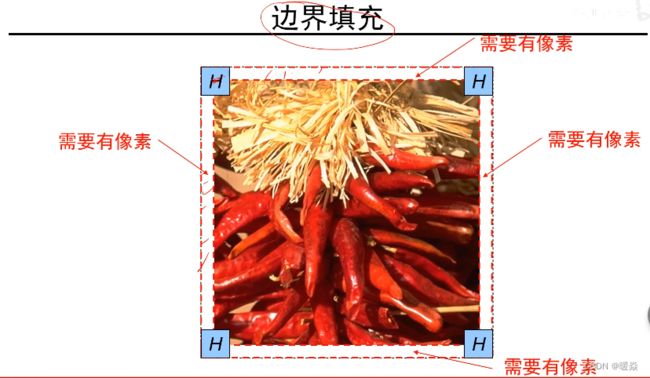
为什么必须边界填充?
如果不进行边界填充,卷积结果的图像比原图像小一圈,卷积操作后的图像要小于输入时图像,通过边界填充,可以实现卷积前后图像的尺寸不变;。

边界填充方法
常数填充
零填充(zero padding)
拉伸
镜像
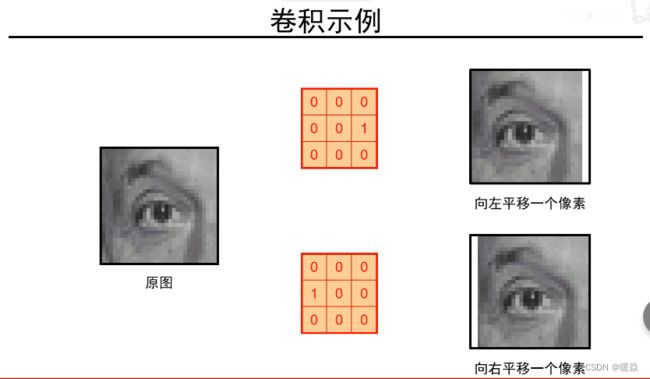
卷积实例
单位脉冲核
锐化
平均卷积核
高斯卷积核
平均卷积核存在的问题
因为是与周围加权平均,所以卷积后的图像产生了一些水平和竖直方向的条状。
其实对于平滑来说,卷积核中权重全都是1/9 ,显然这是不合理的。在这个过程中会损失图像的高频信息产生振铃效应。也就是卷积后的图像产生了一些水平和竖直方向的条状。图像处理中,对一幅图像进行滤波处理,若选用的滤波器具有陡峭(方的,不平滑)的变化,则会使滤波图像产生“振铃”,所谓“振铃”,就是指输出图像的灰度剧烈变化处产生的震荡,就好像钟被敲击后产生的空气震荡。

产生这种现象的原因在于由于卷积过程中引入了本来图像上没有的信息,所以这并不是我们想要的结果,产生这种原因的根源就是因为卷积的模板是方的,也就是卷积核中的权重都是一样的,想要出除这种效应,就需要对卷积的模板进行更换,也即是将卷积核模板调整的更加平滑一些。比如下面这张图,距离中心位置越远相应的权重就应该更小。这样的设置也更加合理一些。这就是高斯核。

高斯卷积核定义
高斯卷积核生成步骤
确定卷积核的尺寸
比如5x5
设置高斯函数的标准差
比如σ=1
计算卷积核各个位置权重值
对权重值进行归一化
需要注意的是在高斯核中,约束条件是所有权重相加和为1,这样做的目的是防止卷积后数据溢出,因为无论RGB还是灰度图都在[0,255]内。当然也不希望所有权重的和小于1,假如是一张全白的图也即是像素值全为255,经过一个33 ,权重都为0.1的卷积核,得到输出结果却是2550.9 ,显然这也不是想要的结果。因此添加限制条件为权重和为1 。
如果卷积后数据溢出,改变了图像原始的0-255的范围。为解决该问题只需要将卷积核归一化即可,也就是卷积核中每一个值除以卷积的总和。
高斯卷积核参数
高斯卷积核参数只有一个,高斯函数标准差σ。窗口尺寸可以由高斯函数标准差σ求出。窗口大小 = 23σ+1。
卷积核尺寸大小(窗口大小)
一般由高斯函数标准差σ求出。窗口大小=23σ+1。
高斯函数标准差σ
其实就是标准差(方差),越大就会散布的越开,也即是窗宽相同,σ越大越扁,σ越小越突出,因为总面积要为1。
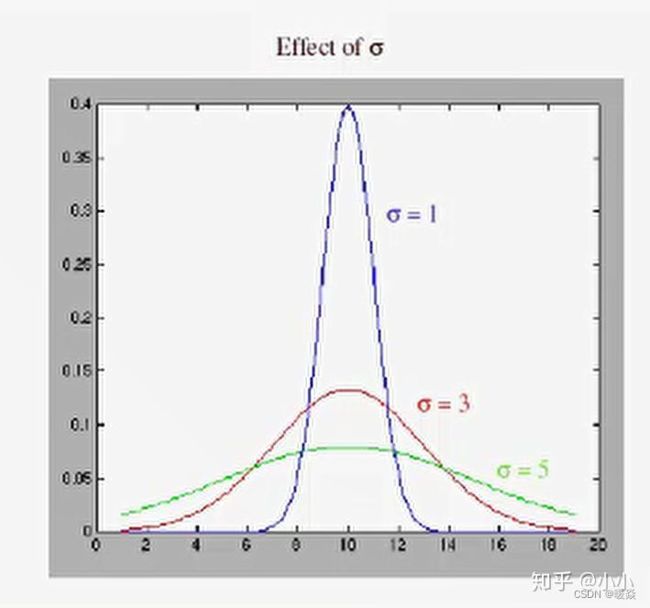
窗宽相同,总面积都为1,则
方差越大,中心权重越小,图像越平滑。
方差越小,中心权重越大,图像越陡峭。

同理,也可以通过固定方差σ去改变窗口大小。
当方差固定时,也就是说这个突出的最高中心点位置是相同的,而总面积又是相同的,归一化操作为(当前值/所有值之和),则
窗口越大,归一化中分子相同,分母越大,中心点权重占比越小,相对周围点权重占比越大,越平滑。
窗口越小,归一化中分子相同,分母越小,中心点权重占比越大,相对周围点权重占比越小,越陡峭。
也就是说当方差固定时,窗口越小平滑的就越不明显,就会导致图像比较模糊。
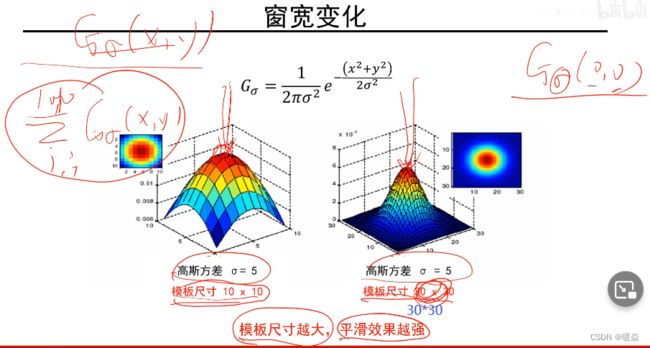
这样一来,就会涉及到两个参数的选取问题,一般来说有个经验性的值。窗口大小为6σ+1。
高斯卷积核参数经验法则
为什么高斯卷积核窗口大小是23σ+1?
遵循3σ原则,基本可以包含99%以上的信号,甚至可以不用归一化。超过[-3σ,3σ]范围的信号很少。
高斯卷积核中心的左边和右边遵循3σ原则,所以是23σ,再加上自身1,所以是23*σ+1。
高斯核注意事项
高斯卷积非线性
高斯卷积核是线性操作。
高斯核权值非负
高斯卷积核的权值不可为负数。
高斯核权值总和为1
恒定区域不受卷积影响。
高斯卷积核作用
低通滤波器
去除图像中的“高频”成分(低通滤波器)。
抑制噪声
实现图像平滑
高斯卷积核分解
大方差卷积分解为多个连续小方差卷积(计算结果不一定相等)
使用多次小方差卷积核连续卷积,可以得到与大方差卷积核相同的结果。
例:高斯卷积对一副图像进行连续两次σ=1的高斯卷积输出结果等价于使用 2 σ \sqrt 2 \sigma 2σ的高斯卷积一次的输出结果。这个满足勾股定理的,比如连续的两次高斯卷积核大小为 2 σ 2 \sigma 2σ, 3 σ 3 \sigma 3σ可以使用 1 3 σ \sqrt 13\sigma 13σ高斯卷积核代替。大致意思就是两个小高斯核的连续卷积可以用一个大的高斯核代替。
二维分解为两个一维(计算结果一定相等)
举个例子解释高斯核分解,假设有一个高斯卷积核与一个3x3大小的图像卷积(不考虑边界填充)得到应该是一个点。那么此时将高斯核拆解为两个一维向量,分别与图像进行卷积操作。它的主要作用就是加速。

高斯卷积核分解的作用(降低算法复杂度)
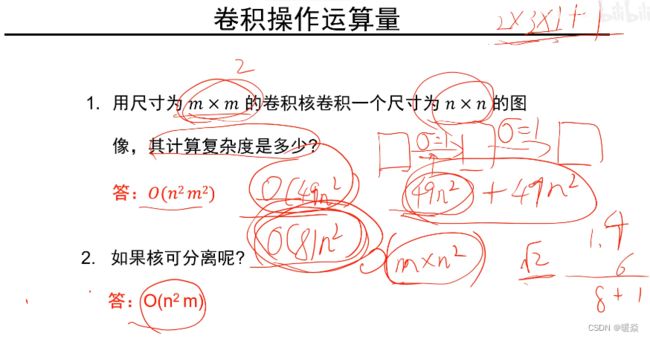
如果使用一个 mxm 的卷积核对一副 nxn 大小的图像进行卷积,考虑边界填充,算法复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2),而使用分解卷积算法复杂度 O ( n 2 m ) O(n^2m) O(n2m) 【其实这是x或者y一个方向上的复杂度】,也就是说如果对核进行分离,那么复杂度就能够降低一个等级,这是一件很有意义的事情。从这里也可以看出来如果使用小核进行卷积也能够加速运算。
参考:机器视觉学习(二)高斯卷积 – 小小
参考:【图像处理】高斯模糊、高斯函数、高斯核、高斯卷积操作 – mjiansun
边缘提取
边缘
图像中亮度明显而急剧变化的点。
为什么研究边缘?
编码图像中的语义与形状信息。
相对于像素表示,边缘表示显然更加紧凑。
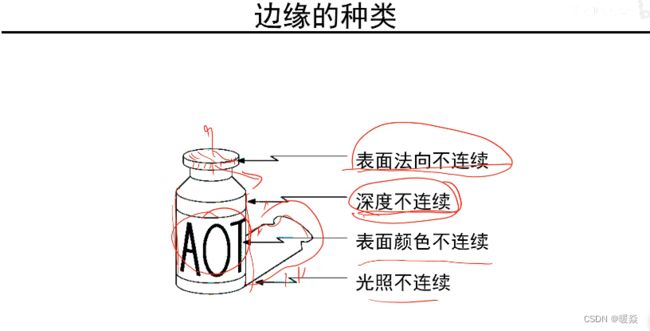
边缘种类
表面法向不连续
深度不连续
真实图片中是不存在的,拍照照到的地方和照不到的地方的边界。
表面颜色不连续
例:识别物体时需考虑,品牌标签等。
光照不连续
边缘检测
图像偏导
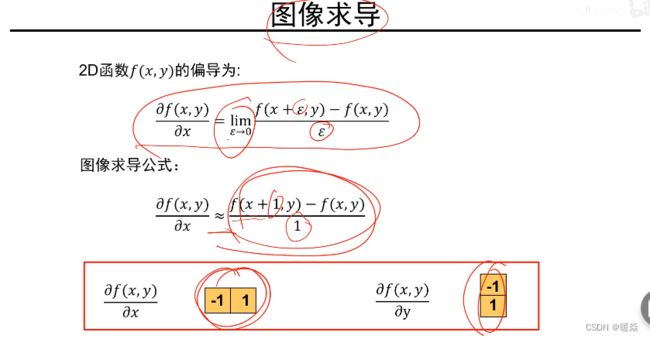

x方向求导,求出来是y方向的边。
y方向求导,求出来是x方向的边。


图像梯度的模
图像梯度的模来反映图像的边缘信息。
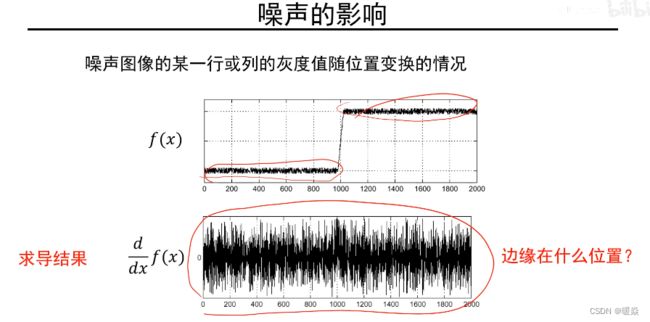
噪声的影响
噪声影响带来的问题
若对灰度函数直接求导,图像中不能确定最大导数位置。
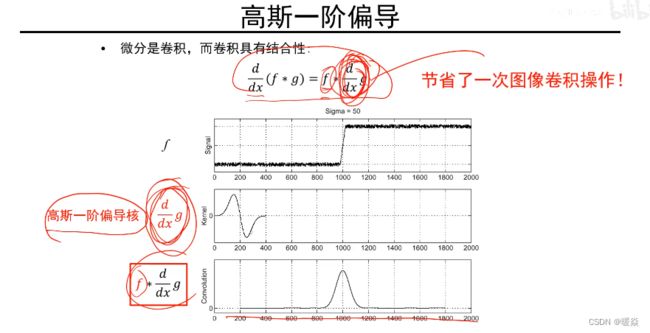
解决办法(先平滑处理)

缺点:需要进行2次卷积操作,一次f*g,一次求x偏导
解决办法:卷积交换律(高斯一阶偏导核)
高斯一阶偏导核
高斯一阶偏导卷积核的方差参数
高斯一阶偏导核注意事项
高斯的导数
卷积核中权值可为负
权值总和为0
恒定区域无响应,即恒定区域不会有边缘。
例如一张全白的图,使用-3|2求导,1*(-3)+1*2=-1,计算结果显示有梯度,与实际不符,因为这是一张全白的图。所以必须使得权值总和为0,保证像这样的情况不出错。
高对比度点的响应值大
边缘检测目标
Canny边缘检测器
高斯一阶偏导核卷积图像
计算每个点的梯度幅值和方向
梯度幅值:用来描述该点是不是边缘
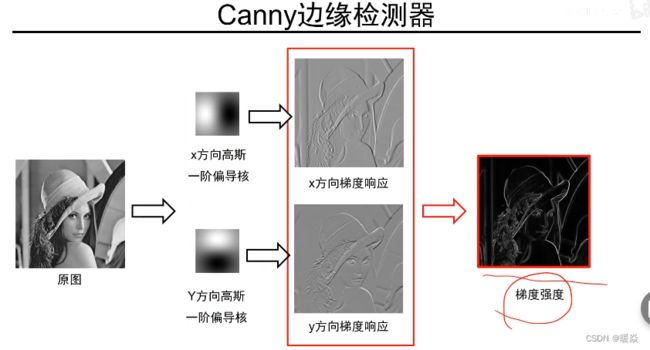
经过高斯一阶偏导核的处理,梯度强度边缘很粗,因为边缘附近的信号,从左到右是慢慢改变的,而不是突然改变的阶梯型,但边缘检测想要更细的边,就需要非极大值抑制。
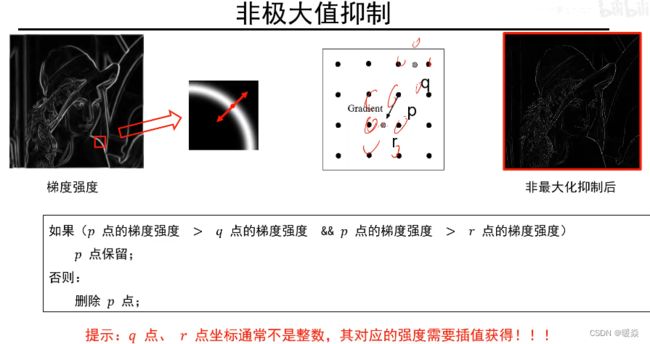
非极大值抑制
p跟梯度方向的正方向距离为1的 r 和反方向距离为1的 q 比较梯度强度。梯度强度p>q&&q>r,则保留p点,否则删除p点。
一般r和q不在图像正规的像素点上,通常r和q点的强度需要周边的点加权求和来获得。
但,非最大化抑制的结果中有噪声,需要通过门限值对噪声进行过滤。
门限过滤
![]()