论文笔记：Fine-Grained Visual Classification via PMG Training of Jigsaw Patches

Fine-Grained Visual Classification via Progressive Multi-Granularity Training of Jigsaw Patches

0 摘要

对哪种粒度最具有区别性以及如何在多粒度之间融合信息所做的工作较少。

本文突出的分类框架：

1. 一种渐进式训练策略，在每个训练步骤都添加新层，以根据最后一步和上一阶段找到的较小粒度信息来利用信息
2. 一个拼图生成器，形成包含不同粒度级别信息的图像（DCL提到的那个方法？）

源代码：https://github.com/RuoyiDu/PMG-Progressive-Multi-Granularity-Training

1 引言

鲜有工作对哪种粒度最有区别的局部区域、如何将跨粒度信息融合在一起以实现分类准确性这两个问题进行研究。

跨粒度的信息有助于避免类内较大变化的影响。仅识别区分性部分通常不够，识别这些部分之间的相互作用方式也不够。

最近的研究集中在“放大”因子[11,36]，即不仅识别零件，而且还聚焦于每个部分内真正有区别的区域。该方法主要集中在几个部分，而忽略了其他部分，也没有考虑如何将不同放大部分特征以协同方式融合在一起。作者认为，不仅需要识别部分及最具区分性的粒度，而且还需要如何有效地合并不同粒度的部分。

既不显示也不隐式地从部分（或其放大版本）挖掘细粒度的特征表示。 而是假设：细粒度的区分性信息自然位于不同的视觉粒度之内，要鼓励网络以不同的粒度进行学习，同时将多粒度特征融合在一起。

提出的框架可同时容纳零件粒度学习和跨粒度特征融合：

1. 渐进训练策略，融合不同粒度特征
2. 随机拼图生成器，鼓励网络学习特定粒度特征

**多粒度渐进式训练框架，以学习不同图像粒度之间的互补信息，在训练过程中按部进行，其中每一步重点是在网络的相应阶段训练特定于粒度的信息。**从更稳定的细粒度开始，逐渐过渡到粗粒度，避免了出现在较大区域中的大型内部类差异所造成的混淆。每个训练步骤结束时，在当前步骤训练的参数将传递到下一个训练步骤作为其参数初始化。

直接应用渐进式训练将不会有益于细粒度特征学习，因为获得的多粒度信息可能倾向于集中在相似区域上。通过引入一个拼图生成器来解决，在每个训练步骤中形成不同的粒度级别，仅最后一步使用原图像训练。 鼓励模型在块级别上工作，其大小特定于特定的粒度。本质上，迫使网络的每个阶段都重点关注局部补丁，而不是整个图像，从而学习特定于给定粒度级别的信息。
本文的主要贡献可归纳如下：

1. 一种渐进式训练策略，以不同的训练步骤进行操作，并且在每个步骤中都融合了先前粒度级别的数据，最终在不同粒度之间训练了固有的互补属性，从而实现了细粒度的特征学习。
2. 一个拼图生成器形成不同级别的粒度
3. 渐进多粒度（PMG）训练框架表现很好

2 相关工作

细粒度分类

从强监督弱监督。弱监督工作中，大多数关注定位部分、互补部分、不同粒度的部分。但如何将这些部分的信息更好地融合在一起很多有人考虑。并且当前的融合技术可以大致分为两类：不同部分各自预测将其概率直接合并，特征合并进行预测。这两种方法都训练一个全连接融合层，将从不同部分提取的特征（图或向量）融合起来。

将不同部分的特征融合起来是一个难题。 本文基于细粒度对象的内在特征来解决这个问题：尽管类内差异大，但细微的细节显示了局部区域的稳定性。因此，引导网络逐步从小粒度到大粒度的特征学习，而不是先定位。

图像分割

通过采用拼图作为弱监督网络的初始化，使网络有更好的转换性能，该方法有助于网络利用图像的空间关系。

在one-shot learning中，图像分割操作用于数据增强，分割两个图像并交换图像块以生成新的训练图像。

DCL通过破坏全局结构来强调局部细节并重构图像以学习局部区域之间的语义相关性。但是，它会在整个训练过程中以相同大小分割图像，这意味着难以利用多粒度区域。

本文应用了一个拼图生成器来限制每个训练步骤中学习区域的粒度。

渐进式训练

该策略允许网络发现图像分布的大规模结构，然后将注意力转移到越来越多的尺度细节上。

本文采用渐进式训练的思想来设计一个可以通过一系列训练阶段学习这些信息的单一网络。

1. 输入图像分割成块以训练模型低层
2. 逐步增加补丁的数量，高层相应的层也添加进入并训练

3 方法

鼓励模型在较浅的层中学习稳定的细粒度信息，并随着训练的进行逐渐将注意力转移到对深层中粗粒度的抽象信息的学习上。

3.1 网络架构

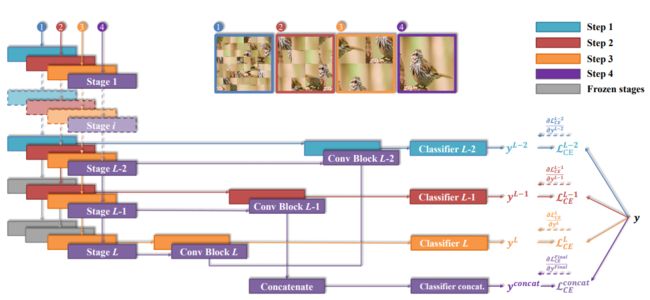
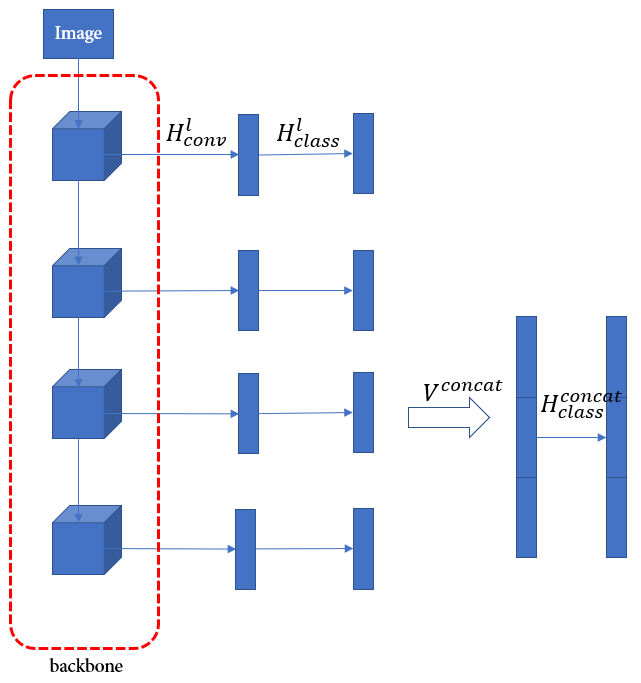
主干网络$F$有$L$个阶段，每个阶段的输出特征图为$F^l\in {\mathbb{R}}^{H_l\times W_l\times C_l}$，$l=\{1,2,...,L\}$。目标是对在不同中间阶段提取的特征图施加分类损失。引入卷积块$H_{conv}^l$将$F^l$的输出作为输入变成为向量表示$V^l=H_{conv}^l(F^l)$，再经过该阶段的分类模块$H_{class}^l$（两个全连接层、BN、Elu（不是ReLU））预测分类得分的概率分布$y^l=H_{class}^l(V^l)$。考虑从后往前的$S$个阶段，即$l=L,L-1,...,L-S+1$。将最后三个阶段的输出拼接起来，即$V^{concat}=concat[V^{L-S+1},...,V^{L-1},V^L]$再经过附加分类模块$y^{concat}=H_{class}^{concat}(V^{concat})$。

3.2 渐进式学习

先训练低阶段，然后逐步增加新阶段。由于低阶的感受野和表示能力受限，网络将被迫从局部细节中利用区分性信息。当特征逐渐发送到高阶段时，模型能够定位从局部细节到全局结构的区分信息。

交叉熵损失：
$$\begin{gathered} {\mathcal{L}}_{CE}(y^l,y)=-\sum _{i=1}^m{y}_i^l\log (y_i^l) \\ {\mathcal{L}}_{CE}(y^{concat},y)=-\sum _{i=1}^m{y}_i^{concat}\log (y_i^{concat}) \end{gathered}$$
在每次迭代中，一批数据$d$将用于$S+1$步，按序在每一步中仅训练一个阶段的输出，而当前预测中使用的所有参数都要优化。

3.3 拼图生成

图片$d\in R^{3\times W\times H}$，分割成$n\times n$块（要整除），随机打乱变成新图片$P(d,n)$。

关于每个阶段的超参数$n$的选择，需要满足两个条件：

1. 块的尺寸小于相应阶段的感受野，否则性能减少
2. 块的尺寸随阶段的感受野的增加成比例地增加。 通常，每个阶段的感受野大约是最后一个阶段的感受野的两倍。 因此，对于第$l$阶段的输出，我们将$n$设置为$2^{L-l+1}$.

训练过程：

1. 将训练数据经过拼图生成器扩充为$P(d,n)$，标签$y$不变。
2. 对第$l$阶段的输出$y^l$，输入批次$P(d，n),n=2L-l+1$，并优化此传播中使用的所有参数。

测试推理阶段：

不经过拼图生成器，仅使用$y^{concat}$，结果$C_1=\arg \max (y^{concat})$。但将所有输出与等权组合在一起时，性能更好，$C_2=\arg \max ({\sum }_{l=L-S+1}^L{y}^l+y^{concat})$。

4 实验

4.1 细节

主干网：VGG16、ResNet50

L=5，S=3，$\alpha =1,\beta =2$（这两个参数是啥不知道）

$550\ast 550$随机裁剪$448\ast 448$、水平翻转。

SGD、lr=0.002，余弦衰减、300epochs，bs=16，wd=0.0005，monmentun=0.9

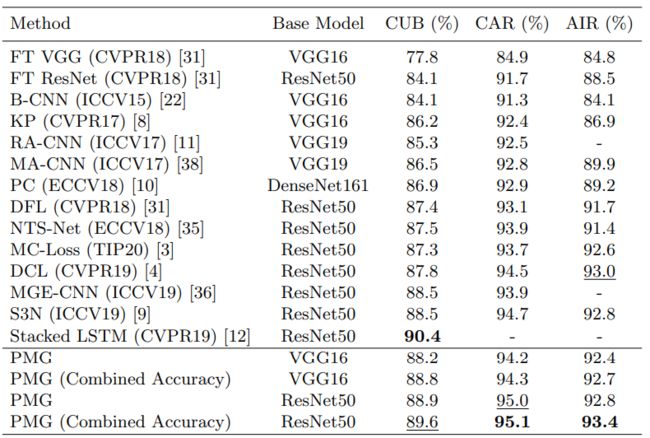
4.2 比较SOTA

4.3 消融实验

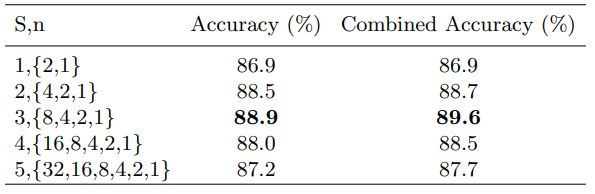
输出S阶段数从1增加到5，没有拼图生成器。y连续保持不变，步数为S + 1。

当$S<4$时，$S$的增加会显着提高模型性能，但之后开始下降。可能的原因是，低阶层主要集中在与类无关的特征上， 但是额外的监督将迫使其查找与班级相关的信息，然后影响整体效果。

拼图生成的效果：

当$S<4$时，提高模型性能。当$S=4$时，模型没有任何优势，而当$S=5$时，降低模型性能。 因为当$n> $8时，块太小无法保留有意义的信息。

4.4 可视化

应用Grad-CAM对方法对基线模型和本文模型的最后三个阶段的卷积层进行可视化处理。结果表明：

1. 模型真正地根据细粒度的可区分部分逐步提供了预测
2. 与基线模型的激活图相比，模型显示出对目标对象的更有意义的集中，而基线模型仅在最后阶段显示了正确的注意力。 这种差异表明，渐进式训练的中间监督可以帮助模型在早期阶段找到有用的信息。
3. 基线模型通常仅在进行预测的最后阶段集中在对象的一个或两个部分上。 但本文关注区域几乎在每个阶段都覆盖了整个对象，这表明拼图生成器生成的图像可以迫使模型在每个粒度级别上学习更多可辨别的部分。

5 结论

本文将渐进式训练策略应用于细粒度的分类任务，并提出了渐进式多粒度（PMG）训练框架，该框架包含两个主要组成部分：

1. 渐进方式融合了多粒度特征的训练策略
2. 拼图生成器，以形成包含不同粒度级别信息的图像。

端到端训练，而无需额外信息，测试单一网络传播即可。

三个数据集进行了实验，其中两个获得了最先进的性能，而另一个获得了竞争性结果。

6 代码

这篇论文的代码很简单：

拼图生成：

def jigsaw_generator(images, n):
    l = [[a, b] for a in range(n) for b in range(n)]  # 块的序号
    block_size = 448 // n  # 块的大小，这里的448是图片大小
    rounds = n ** 2  # 块的总数
    random.shuffle(l) # 打乱索引
    jigsaws = images.clone() # 防止对原图像影响
    for i in range(rounds):
        x, y = l[i]  # 交换
        temp = jigsaws[..., 0:block_size, 0:block_size].clone()  # 利用第一块的位置反复进行交换
        jigsaws[..., 0:block_size, 0:block_size] = jigsaws[..., x * block_size:(x + 1) * block_size, y * block_size:(y + 1) * block_size].clone()
        jigsaws[..., x * block_size:(x + 1) * block_size, y * block_size:(y + 1) * block_size] = temp
    return jigsaws