数学建模笔记-第五讲-相关系数

相关系数

衡量两个变量之间相关性大小的指标

• 通过样本统计量来估计总体统计量

pearson相关系数

• 协方差与量纲有关
• pearson相关系数可以看作是变量标准化之后的协方差
  • 
  • 这里框框里应该还要减一个（标准化后变量的）均值的，而这个均值是0
• 总体pearson相关系数

• pearson相关系数绝对值<1
• 样本pearson相关系数
• 基本一样，就是把总体的均值和标准差变成了样本的均值和标准差
  • 而样本的方差分母为n-1，这就是最大的区别，无偏估计
  • 概率论与数理统计的知识点

相关性可视化

绝对值越接近1，越有线性

误区

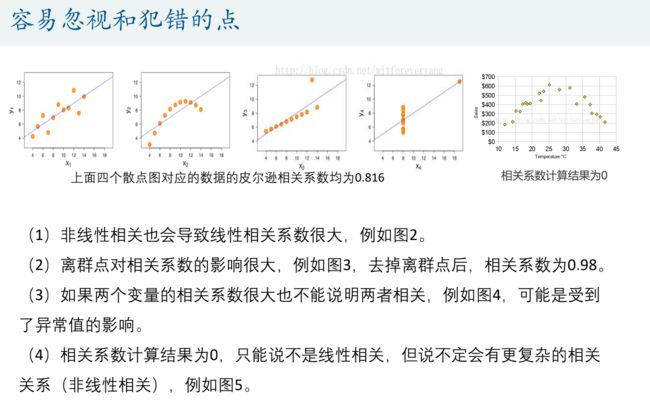
很重要！必须要画出散点图，证明变量之间是有线性关系的，才能用皮尔逊相关系数来说明线性相关性

• 重点

• 四个错误
• 非线性相关也会导致皮尔逊相关系数很大
• 离群点影响很大
• 皮尔逊相关系数大也不能说明了两者相关
• 相关系数为0可能也存在非线性关系，不能说没关系

• 总结

写论文时先画出散点图，证明有线性关系，再用皮尔逊相关系数说明其相关性。

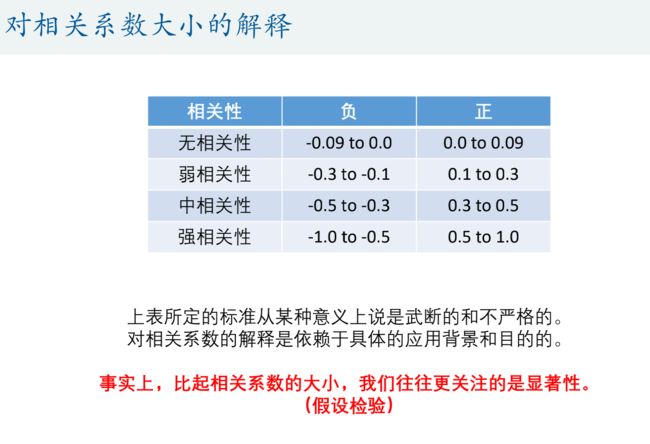
相关系数大小的解释

这个强弱根据具体的题目来定，需要精密的时候可以定严格一点，比如>0.9的才算强相关性

例题

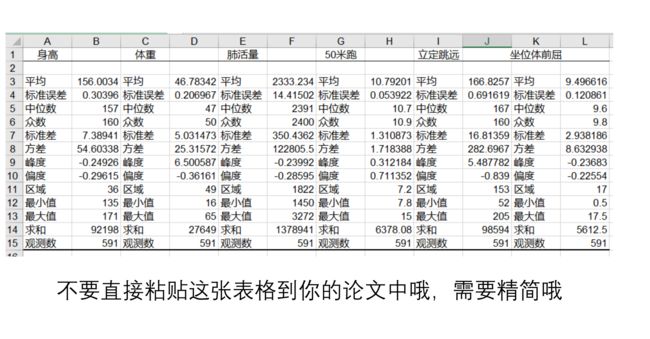
描述性统计

论文中我们需要把这些数组的描述性统计做成表格写出来

特别是标粗的统计量

• 这些函数默认是按列计算的
• 若要按行，函数第二个参数改为1

matlab

clear;clc
load 'physical fitness test.mat'  %文件名如果有空格隔开，那么需要加引号
% https://ww2.mathworks.cn/help/matlab/ref/corrcoef.html
%% 统计描述
MIN = min(Test);  % 每一列的最小值
MAX = max(Test);   % 每一列的最大值
MEAN = mean(Test);  % 每一列的均值
MEDIAN = median(Test);  %每一列的中位数
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test);  %每一列的峰度
STD = std(Test);  % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]  %将这些统计量放到一个矩阵中表示

• 文件名如果有空格隔开，那么需要加引号

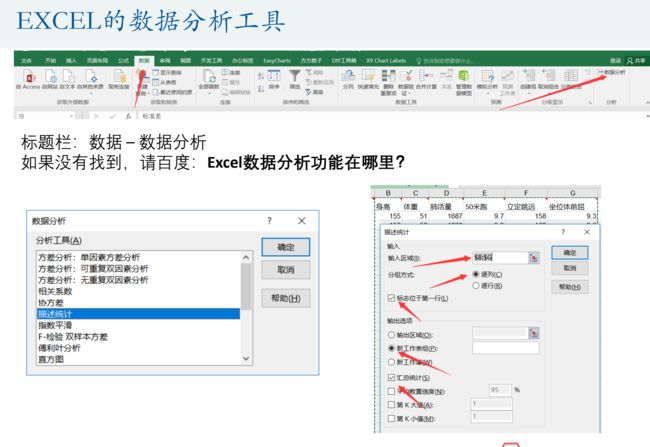
excel

excel数据分析 描述统计 勾选汇总统计 结果需要精简处理

SPSS

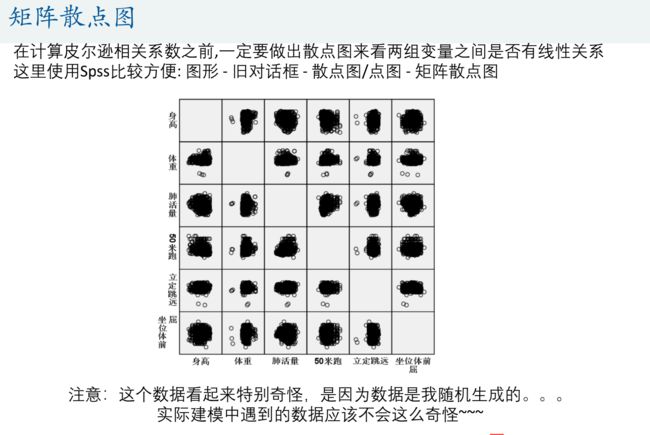
矩阵散点图

当需要变量两两组合看是否有线性关系时，可以用SPSS做矩阵散点图

计算相关系数

热力图美化结果

• excel

• matlab、python也有相应的方法，自行查阅

对相关系数进行假设检验

假设检验知识点简单记录

• 关于假设检验的知识

• 在概率论与数理统计和统计学两门课，我已经学过有关知识了，就没听清风的这部分

• 双侧检验步骤

• 单侧检验步骤大差不差

• 实际上构造什么分布是最难的，涉及到非常复杂的证明

• 用的时候只要知道怎么用就行，对于什么检验统计量用什么分布，是数学家探索发现的

• 如何变成实现

  • 这样判断还是挺麻烦的，要求导啥的
  • 用p值是推荐的
  • 双侧检验的p值是单侧检验的两倍，要乘2再跟0.05比较（95%）

• 步骤

  • 确定原假设和备择假设
  • 原假设成立条件下构造统计量
  • 计算检验值（带入计算的值），以及对应的P值
  • 比较P值与0.05的关系
    • 大于0.05，接受H0
    • 小于0.05，拒绝H0

皮尔逊相关系数的假设检验

我们通过检验相关系数的显著性，来说明相关系数有没有意义

• 原假设H0:r=0
• 构造符合某一分布的统计量（要检验的量的一个函数，不包含其他随机变量），这里用的是t分布
• n趋于无穷的时候，t分布实际上就是标准正态分布

• 计算检验值，然后要看检验值落在接受域，还是拒绝域
• 画图：tpdf()函数就是t分布的函数，第一个参数是自变量，第二个参数是自由度(n-2)

链接：t分布查表文档

双侧检验，置信水平α=0.05

那么要找$t_{1-\frac{\alpha }{2}}=t_{0.975}$这一列，再按自由度28找到行。找到临界值2.048

• 得到结论

更好的方法：P值判断法

前面的过程还是太为繁琐了，我们用P值更好的检验显著性

• tcdf():t分布的累计密度函数
• 这里乘2是因为双侧检验
• 得到最后计算的P值
• 说明能否拒绝原假设
• 论文中:显著性标记
  • 没有*：不显著
  • *：90%水平上显著
  • **：95%水平上显著
  • ***：99%水平上显著

• MATLAB计算p值

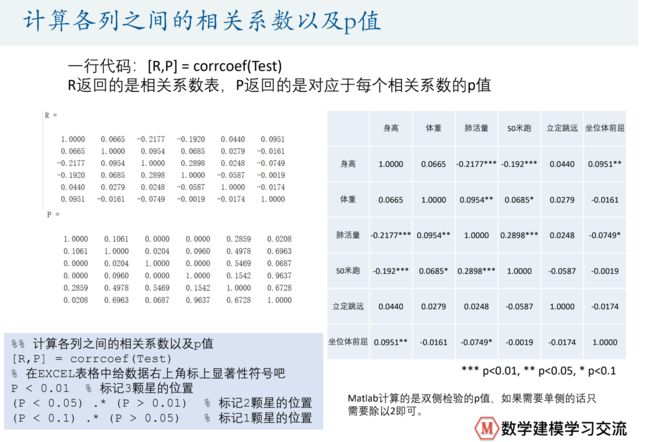
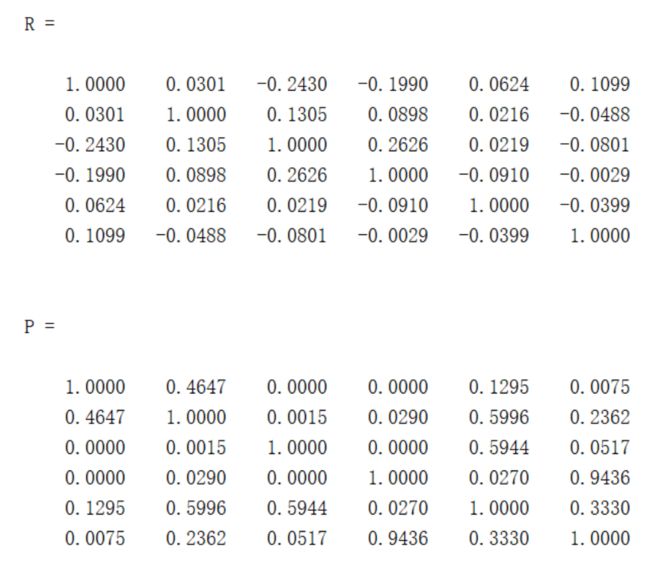
一行代码：[R,P] = corrcoef(Test)

R返回的是相关系数表，P返回的是对应于每个相关系数的p值

%% 计算各列之间的相关系数
% 在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系
% 这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图

R = corrcoef(Test)   % correlation coefficient


%% 假设检验部分
x = -4:0.1:4;
y = tpdf(x,28);  %求t分布的概率密度值 28是自由度  
figure(1)
plot(x,y,'-')
grid on  % 在画出的图上加上网格线
hold on  % 保留原来的图，以便继续在上面操作
% matlab可以求出临界值，函数如下
tinv(0.975,28)    %    2.0484
% 这个函数是累积密度函数cdf的反函数
plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')


%% 计算p值
x = -4:0.1:4;
y = tpdf(x,28);
figure(2)
plot(x,y,'-')
grid on 
hold on
% 画线段的方法
plot([-3.055,-3.055],[0,tpdf(-3.055,28)],'r-')
plot([3.055,3.055],[0,tpdf(3.055,28)],'r-')
disp('该检验值对应的p值为：')
disp((1-tcdf(3.055,28))*2)  %双侧检验的p值要乘以2

%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号吧
P < 0.01  % 标记3颗星的位置
(P < 0.05) .* (P > 0.01)  % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置
% 也可以使用Spss操作哦 看我演示

SPSS中操作：分析->相关->双变量->选中指标->勾选皮尔逊相关系数、勾选双尾(双侧检验)、勾选显著相关性(显著性标记)

1. 最后要加上*** p<0.01, ** p<0.05, * p<0.1

2. Matlab计算的是双侧检验的p值，如果需要单侧的话只
   需要除以2即可。

皮尔逊相关系数假设检验的条件

一个重要的部分：进行假设检验的前提

• 第一个正态分布检验是要进行的
• 后两个是默认的

正态分布检验

• 偏度和峰度

%% 正态分布检验
% 正态分布的偏度和峰度
x = normrnd(2,3,100,1);   % 生成100*1的随机向量，每个元素是均值为2，标准差为3的正态分布
skewness(x)  %偏度
kurtosis(x)  %峰度
qqplot(x)

大样本JB检验

• 雅克—贝拉检验

• 步骤

  • 确定样本量>30

  • 确定原假设和备择假设

  • 计算偏度和峰度，带入计算统计量，计算相应p值

  • 得出结论

• MATLAB中操作
  • [h,p] = jbtest(x,alpha)
  • 这里x只能是向量，所以只能一列一列进行检验
  • 写一个循环

% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
[h,p] = jbtest(Test(:,1),0.01)

% 用循环检验所有列的数据
n_c = size(Test,2);  % number of column 数据的列数
H = zeros(1,6);  % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
    [h,p] = jbtest(Test(:,i),0.05);
    H(i)=h;
    P(i)=p;
end
disp(H)
disp(P)

% Q-Q图
qqplot(Test(:,1))

• 初始化保存结果的矩阵，可以节省运行时间
• 我们计算出来发现，每列都拒绝原假设，说明每列数据全都不满足正态分布，说明前面假设检验那些显著性是没用的

小样本Shapiro-wilk检验

小样本才能用

该检验原理较为复杂，我们只要会用就习惯

matlab没有这个相关函数，所以用spss

分析 - 描述统计 - 探索

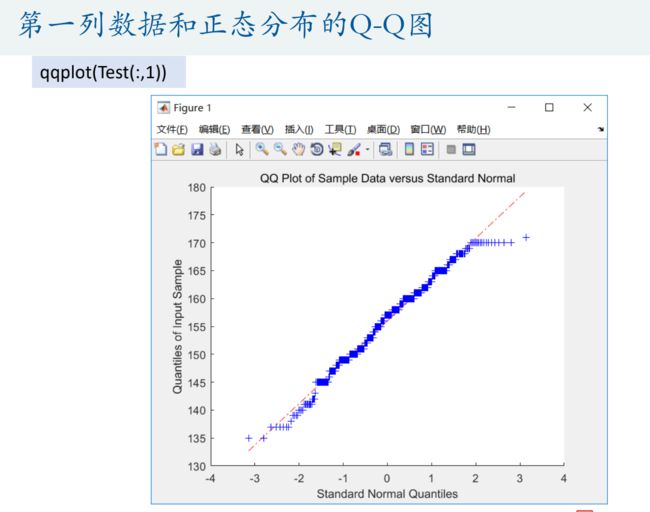
QQ图

用QQ图来看是否符合正态分布

​ 在统计学中，Q‐Q图（Q代表分位数Quantile）是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。
​ 首先选定分位数的对应概率区间集合，在此概率区间上，点(x,y)对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。
​ 这里，我们选择正态分布和要检验的随机变量，并对其做出QQ图，可想而知，如果要检验的随机变量是正态分布，那么QQ图就是一条直线。
​ 要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点是否近似地在一条直线附近。（要求数据量非常大）

• 演示

• 要求样本量比较大，起码几百，才能用于判断
• 最好还是区分大样本还是小样本，然后选择前两种检验

第一个总结

正确在论文中使用皮尔逊相关系数

• 对数据做一个描述性统计
• 做散点图判断是否有线性关系，如果有那么就可以用皮尔逊相关系数
• 如果要检验相关系数是否显著，对其进行假设检验，那么就要做一个正态性检验
• 如果数据符合正态分布，就可以计算一系列p值，看系数是否是显著的
• 万一没有通过正态性检验，那么就用下面的斯皮尔曼相关系数

斯皮尔曼spearman相关系数

对数据的要求比较低，没有总体要是正态分布的前提

定义

• 给数据排序，计算等级。
• 等级就是排序，如果有两个一样的，就取排序的平均值

• 极端情况下
  • 每组数据X的等级和Y的等级都相同，那么等级差全是0，计算出的r=1
  • 每组数据X和Y的等级刚好全是相反的，一个从大到小，一个从小到大，那么最后算出来r=-1
  • 可以证明r位于[-1,1]之间
• 意义
  • >0正相关
  • <0负相关
  • 绝对值越大，相关性越强

另一种定义

斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数

• 因为前面有等级相等取平均值，所以结果有细微的区别

MATLAB计算

两种用法

• corr()就是一个能求很多种相关系数的函数，这里type参数为’Spearman’
• 数据必须是列向量或者一个矩阵

1. corr(X , Y , 'type','Spearman')
   这里的X和Y必须是列向量哦~
2. corr(X, 'type' , 'Spearman')
   这时计算X矩阵各列之间的斯皮尔曼相关系数

%% 斯皮尔曼相关系数
X = [3 8 4 7 2]'  % 一定要是列向量哦，一撇'表示求转置
Y = [5 10 9 10 6]'
% 计算矩阵各列的斯皮尔曼相关系数
R = corr(Test, 'type' , 'Spearman')

• 跟刚才皮尔逊相关系数结果对比

斯皮尔曼相关系数的假设检验

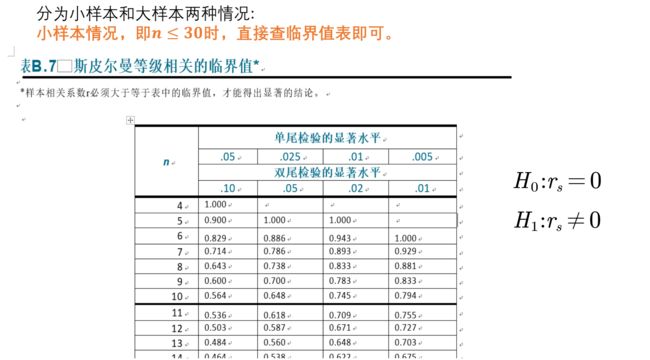
小样本n<=30

直接查表

一般就是找双侧检验0.05这一列，通过样本量找到表中临界值

表在资料中

必须要计算出来的>表中临界值，落在拒绝域中，才能说明显著性

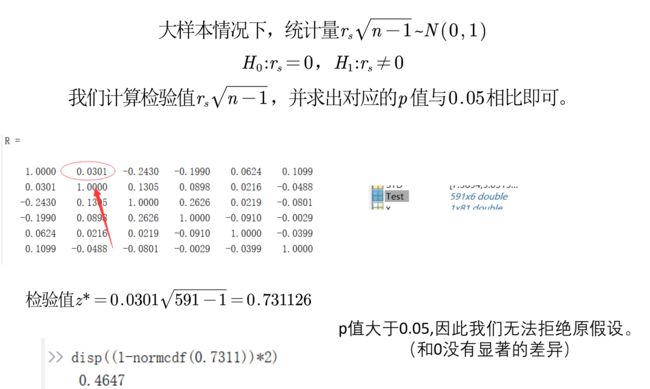
大样本

p值就是右边那块红色区域的面积

下结论：p值大于0.05,因此我们无法拒绝原假设。
（和0没有显著的差异）

MARLAB中假设检验

% 直接给出相关系数和p值
[R,P]=corr(Test, 'type' , 'Spearman')

• 结果

• 结果画表

把皮尔逊和斯皮尔曼相关系数都勾选上，会有两个表

• 表格修改一下放入论文中
  • 只要相关系数就行，已经标注了显著性，其他行可以删掉

第二个总结：两种相关系数比较

• 满足上述三个条件就用皮尔逊
• 其他的用斯皮尔曼

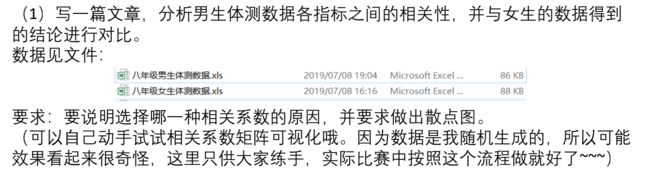
课后作业

本笔记来自清风老师的数学建模，强烈推荐该课程！