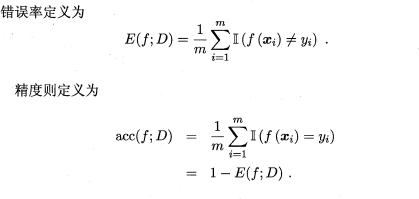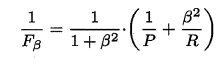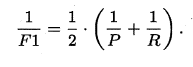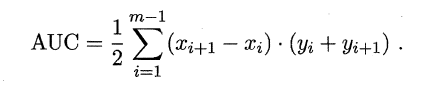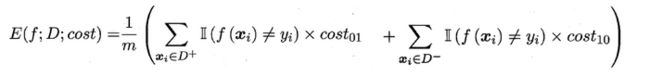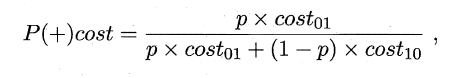【进阶版】机器学习之模型性能度量及比较检验和偏差与方差总结（02）

欢迎订阅本专栏，持续更新中~

本专栏包含大量代码项目，适用于毕业设计方向选取和实现、科研项目代码指导，每一篇文章都是通过原理讲解+代码实战进行思路构建的，如果有需要这方面的指导可以私信博主，获取相关资源及指导！

本专栏前期文章介绍！

机器学习算法知识、数据预处理、特征工程、模型评估——原理+案例+代码实战

机器学习之Python开源教程——专栏介绍及理论知识概述
机器学习框架及评估指标详解
Python监督学习之分类算法的概述
数据预处理之数据清理，数据集成，数据规约，数据变化和离散化
特征工程之One-Hot编码、label-encoding、自定义编码
卡方分箱、KS分箱、最优IV分箱、树结构分箱、自定义分箱
特征选取之单变量统计、基于模型选择、迭代选择

机器学习八大经典分类万能算法——代码+案例项目开源、可直接应用于毕设+科研项目

机器学习分类算法之朴素贝叶斯
【万字详解·附代码】机器学习分类算法之K近邻（KNN）
《全网最强》详解机器学习分类算法之决策树（附可视化和代码）
机器学习分类算法之支持向量机
机器学习分类算法之Logistic 回归（逻辑回归）
机器学习分类算法之随机森林（集成学习算法）
机器学习分类算法之XGBoost（集成学习算法）
机器学习分类算法之LightGBM（梯度提升框架）

机器学习自然语言、推荐算法等领域知识——代码案例开源、可直接应用于毕设+科研项目

【原理+代码】Python实现Topsis分析法（优劣解距离法）
机器学习推荐算法之关联规则（Apriori）——支持度；置信度；提升度
机器学习推荐算法之关联规则Apriori与FP-Growth算法详解
机器学习推荐算法之协同过滤（基于用户）【案例+代码】
机器学习推荐算法之协同过滤（基于物品）【案例+代码】
预测模型构建利器——基于logistic的列线图（R语言）
基于surprise模块快速搭建旅游产品推荐系统（代码+原理）
机器学习自然语言处理之英文NLTK（代码+原理）
机器学习之自然语言处理——中文分词jieba库详解（代码+原理）
机器学习之自然语言处理——基于TfidfVectorizer和CountVectorizer及word2vec构建词向量矩阵（代码+原理）

机器学习配套资源推送

专栏配套资源推荐——部分展示（有需要可去对应文章或者评论区查看，可做毕设、科研参考资料）

自然语言处理之文本分类及文本情感分析资源大全（含代码及其数据，可用于毕设参考！）
基于Word2Vec构建多种主题分类模型（贝叶斯、KNN、随机森林、决策树、支持向量机、SGD、逻辑回归、XGBoost…）
基于Word2Vec向量化的新闻分本分类.ipynb
智能词云算法（一键化展示不同类型的词云图）运行生成HTML文件
协同过滤推荐系统资源（基于用户-物品-Surprise）等案例操作代码及讲解
Python机器学习关联规则资源（apriori算法、fpgrowth算法）原理讲解
机器学习-推荐系统（基于用户）.ipynb
机器学习-推荐系统（基于物品）.ipynb
旅游消费数据集——包含用户id，用户评分、产品类别、产品名称等指标，可以作为推荐系统的数据集案例

进阶版机器学习文章更新~

【进阶版】机器学习之基本术语及模评估与选择概念总结（01）

---

前期我们对机器学习的基础知识，从基础的概念到实用的代码实战演练，并且系统的了解了机器学习在分类算法上面的应用，同时也对机器学习的准备知识有了一个相当大的了解度，而且还拓展了一系列知识，如推荐算法、文本处理、图像处理。以及交叉学科的应用，那么前期你如果认真的了解了这些知识，并加以利用和实现，相信你已经对机器学习有了一个“量”的认识，接下来的，我将带你继续学习机器学习学习，并且全方位，系统性的了解和深入机器学习领域，达到一个“质”的变化。

---

点击下方下载高清版学习知识图册

机器学习Python算法知识点大全，包含sklearn中的机器学习模型和Python预处理的pandas和numpy知识点

---

在上一篇中，我们解决了评估学习器泛化性能的方法，即用测试集的“测试误差”作为“泛化误差”的近似，当我们划分好训练/测试集后，那如何计算“测试误差”呢？

这就是性能度量，例如：均方差，错误率等，即“测试误差”的一个评价标准。有了评估方法和性能度量，就可以计算出学习器的“测试误差”，但由于“测试误差”受到很多因素的影响，例如：算法随机性或测试集本身的选择，那如何对两个或多个学习器的性能度量结果做比较呢？

这就是比较检验。最后偏差与方差是解释学习器泛化性能的一种重要工具。

性能度量

性能度量（performance measure）是衡量模型泛化能力的评价标准，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果。

最常见的性能度量

在回归任务中，即预测连续值的问题，最常用的性能度量是“均方误差”（mean squared error）,很多的经典算法都是采用了MSE作为评价函数，想必大家都十分熟悉。

在分类任务中，即预测离散值的问题，最常用的是错误率和精度，错误率是分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占样本总数的比例，易知：错误率+精度=1。

查准率/查全率/F1

错误率和精度虽然常用，但不能满足所有的需求，例如：在推荐系统中，我们只关心推送给用户的内容用户是否感兴趣（即查准率），或者说所有用户感兴趣的内容我们推送出来了多少（即查全率）。因此，使用查准/查全率更适合描述这类问题。

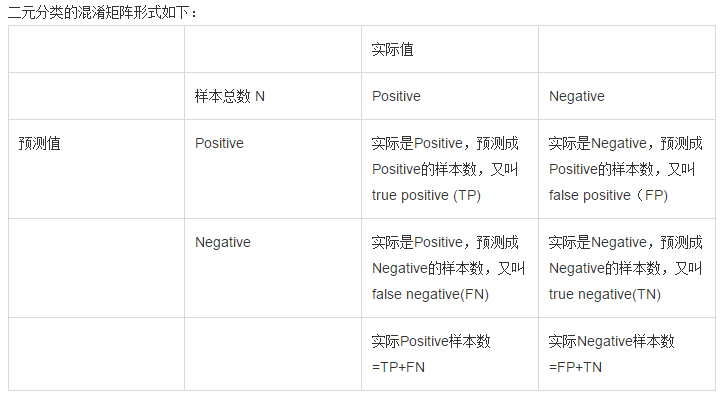
对于二分类问题，分类结果混淆矩阵与查准/查全率定义如下：

初次接触时，FN与FP很难正确的理解，按照惯性思维容易把FN理解成：False->Negtive，即将错的预测为错的，这样FN和TN就反了，后来找到一张图，描述得很详细，为方便理解，把这张图也贴在了下边：

正如天下没有免费的午餐，查准率和查全率是一对矛盾的度量。

例如我们想让推送的内容尽可能用户全都感兴趣，那只能推送我们把握高的内容，这样就漏掉了一些用户感兴趣的内容，查全率就低了；如果想让用户感兴趣的内容都被推送，那只有将所有内容都推送上，宁可错杀一千，不可放过一个，这样查准率就很低了。

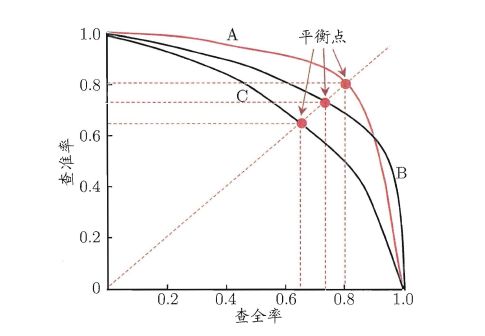
**“P-R曲线”**正是描述查准/查全率变化的曲线，P-R曲线定义如下：根据学习器的预测结果（一般为一个实值或概率）对测试样本进行排序，将最可能是“正例”的样本排在前面，最不可能是“正例”的排在后面，按此顺序逐个把样本作为“正例”进行预测，每次计算出当前的P值和R值，如下图所示：

P-R曲线如何评估呢？若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全包住，则称：B的性能优于A。若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。但一般来说，曲线下的面积是很难进行估算的，所以衍生出了“平衡点”（Break-Event Point，简称BEP），即当P=R时的取值，平衡点的取值越高，性能更优。

P和R指标有时会出现矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure，又称F-Score。F-Measure是P和R的加权调和平均，即：

特别地，当β=1时，也就是常见的F1度量，是P和R的调和平均，当F1较高时，模型的性能越好。

有时候我们会有多个二分类混淆矩阵，例如：多次训练或者在多个数据集上训练，那么估算全局性能的方法有两种，分为宏观和微观。简单理解，宏观就是先算出每个混淆矩阵的P值和R值，然后取得平均P值macro-P和平均R值macro-R，在算出Fβ或F1，而微观则是计算出混淆矩阵的平均TP、FP、TN、FN，接着进行计算P、R，进而求出Fβ或F1。

ROC与AUC

如上所述：学习器对测试样本的评估结果一般为一个实值或概率，设定一个阈值，大于阈值为正例，小于阈值为负例，因此这个实值的好坏直接决定了学习器的泛化性能，若将这些实值排序，则排序的好坏决定了学习器的性能高低。

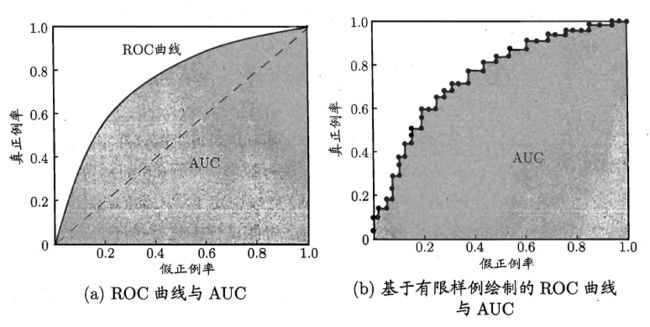
ROC曲线正是从这个角度出发来研究学习器的泛化性能，ROC曲线与P-R曲线十分类似，都是按照排序的顺序逐一按照正例预测，不同的是ROC曲线以“真正例率”（True Positive Rate，简称TPR）为横轴，纵轴为“假正例率”（False Positive Rate，简称FPR），ROC偏重研究基于测试样本评估值的排序好坏。

在二分类的模型项目中，使用较多

简单分析图像，可以得知：当FN=0时，TN也必须0，反之也成立，我们可以画一个队列，试着使用不同的截断点（即阈值）去分割队列，来分析曲线的形状，（0,0）表示将所有的样本预测为负例，

（1,1）则表示将所有的样本预测为正例，（0,1）表示正例全部出现在负例之前的理想情况，（1,0）则表示负例全部出现在正例之前的最差情况。限于篇幅，这里不再论述。

现实中的任务通常都是有限个测试样本，因此只能绘制出近似ROC曲线。

绘制方法：首先根据测试样本的评估值对测试样本排序，接着按照以下规则进行绘制。

在前期的文章当中，也给出了比较详细的代码模板，就可以调用

同样地，进行模型的性能比较时，若一个学习器A的ROC曲线被另一个学习器B的ROC曲线完全包住，则称B的性能优于A。若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。

ROC曲线下的面积定义为AUC（Area Uder ROC Curve），不同于P-R的是，这里的AUC是可估算的，即AOC曲线下每一个小矩形的面积之和。

易知：AUC越大，证明排序的质量越好，AUC为1时，证明所有正例排在了负例的前面，AUC为0时，所有的负例排在了正例的前面。

代价敏感错误率与代价曲线

上面的方法中，将学习器的犯错同等对待，但在现实生活中，将正例预测成假例与将假例预测成正例的代价常常是不一样的

例如：将无疾病–>有疾病只是增多了检查，但有疾病–>无疾病却是增加了生命危险。

以二分类为例，由此引入了“代价矩阵”（cost matrix）。

在非均等错误代价下，我们希望的是最小化“总体代价”，这样“代价敏感”的错误率

同样对于ROC曲线，在非均等错误代价下，演变成了“代价曲线”，代价曲线横轴是取值在[0,1]之间的正例概率代价，式中p表示正例的概率，纵轴是取值为[0,1]的归一化代价。

代价曲线的绘制很简单：设ROC曲线上一点的坐标为(TPR，FPR) ，则可相应计算出FNR，然后在代价平面上绘制一条从(0，FPR) 到(1，FNR) 的线段，线段下的面积即表示了该条件下的期望总体代价；如此将ROC 曲线土的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如图所示：

本文的相关知识的代码实现，均可在《机器学习框架及评估指标详解》找到代码

比较检验

在比较学习器泛化性能的过程中，统计假设检验（hypothesis test）为学习器性能比较提供了重要依据，即若A在某测试集上的性能优于B，那A学习器比B好的把握有多大。 为

假设检验

“假设”指的是对样本总体的分布或已知分布中某个参数值的一种猜想， 例如：假设总体服从泊松分布，或假设正态总体的期望u=u0

我们可以通过测试获得测试错误率，但直观上测试错误率和泛化错误率相差不会太远，因此可以通过测试错误率来推测泛化错误率的分布，这就是一种假设检验。

交叉验证t检验

McNemar检验

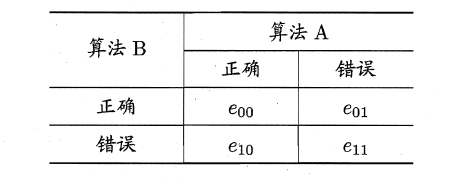
MaNemar主要用于二分类问题，与成对t检验一样也是用于比较两个学习器的性能大小。

主要思想是：若两学习器的性能相同，则A预测正确B预测错误数应等于B预测错误A预测正确数，即e01=e10，且|e01-e10|服从N（1，e01+e10）分布。

因此，如下所示的变量服从自由度为1的卡方分布，即服从标准正态分布N（0,1）的随机变量的平方和，下式只有一个变量，故自由度为1，检验的方法同上：做出假设–>求出满足显著度的临界点–>给出拒绝域–>验证假设。

Friedman检验与Nemenyi后续检验

上述的三种检验都只能在一组数据集上

F检验则可以在多组数据集进行多个学习器性能的比较，基本思想是在同一组数据集上，根据测试结果（例：测试错误率）对学习器的性能进行排序，赋予序值1,2,3…，相同则平分序值，如下图所示：

若学习器的性能相同，则它们的平均序值应该相同，且第i个算法的平均序值ri服从正态分布N（（k+1）/2，（k+1）(k-1)/12），则有：

服从自由度为k-1和(k-1)(N-1)的F分布。下面是F检验常用的临界值：

若“H0：所有算法的性能相同”这个假设被拒绝，则需要进行后续检验，来得到具体的算法之间的差异。常用的就是Nemenyi后续检验。Nemenyi检验计算出平均序值差别的临界值域，下表是常用的qa值，若两个算法的平均序值差超出了临界值域CD，则相应的置信度1-α拒绝“两个算法性能相同”的假设。

偏差与方差

偏差-方差分解是解释学习器泛化性能的重要工具。

在学习算法中，偏差指的是预测的期望值与真实值的偏差，方差则是每一次预测值与预测值得期望之间的差均方。实际上，偏差体现了学习器预测的准确度，而方差体现了学习器预测的稳定性。通过对泛化误差的进行分解，可以得到：

• 期望泛化误差=方差+偏差
• 偏差刻画学习器的拟合能力
• 方差体现学习器的稳定性

易知：方差和偏差具有矛盾性，这就是常说的偏差-方差窘境（bias-variance dilamma），随着训练程度的提升，期望预测值与真实值之间的差异越来越小，即偏差越来越小，但是另一方面，随着训练程度加大，学习算法对数据集的波动越来越敏感，方差值越来越大。

换句话说：在欠拟合时，偏差主导泛化误差，而训练到一定程度后，偏差越来越小，方差主导了泛化误差。因此训练也不要贪杯，适度辄止。

每文一语

现在不是去想缺少什么的时候，该想一想凭现有的东西你能做什么。