《神经网络与深度学习》-卷积神经网络
卷积神经网络
-
- 1. 卷积
-
- 1.1 互相关
- 1.2 卷积的变种
-
- 1.2.1 转置卷积
- 1.2.2 空洞卷积
- 1.3 卷积的数学性质
-
- 1.3.1 交换性
- 1.3.2 导数
- 2. 卷积神经网络
-
- 2.1 用卷积代替全连接
- 2.2 卷积层
- 2.3 汇聚层(池化层)
- 2.4 典型的卷积网络结构
- 3 参数学习
-
- 3.1 误差项的计算
- 4 典型的卷积神经网络
-
- 4.1 LeNet-5
- 4.2 AlexNet
- 4.3 Inception
- 4.4 残差网络
利用全连接前馈网络处理图像时的问题:
(1)参数太多:
对于输入的1001003的RGB图像,全连接前馈网络,第一个隐藏层的每个神经元到输入层有1001003=30000个独立的连接,即权重参数,隐藏层神经元个数增加,参数规模急剧增加,网络训练效率低,易过拟合。
(2)局部不变性特征:
全连接网络很难提取自然图像中的局部不变性特征:尺度缩放、平移、旋转;这些操作不影响自然图像的语义信息。
卷积神经网络
CNN三个结构特性:局部连接、权重共享、汇聚
这三特性使CNN具有一定的平移、缩放、旋转不变性。参数更少。
感受野
卷积神经网络(CNN)收生物学感受野机制得来。感受野指视觉、听觉系统中的一些神经元只接受其支配的刺激区域内的信号。一个神经元的感受野指视网膜上特定的区域,只有这个区域的刺激才能激活该神经元。
1. 卷积
一维卷积
假设一个信号发生器每个时刻 t t t 产生一个信号 x t x_t xt,其信息的衰减率为 w k w_k wk,即在 − 1 个时间步长后,信息为原来的 w k w_k wk 倍.我们把 w 1 , w 2 , w 3 , ⋯ w_1, w_2, w_3, ⋯ w1,w2,w3,⋯称为滤波器(Filter)或卷积(Convolution Kernel). 假设滤波器长度为,它和一个信号序列 x 1 , x 2 , ⋯ x_1, x_2, ⋯ x1,x2,⋯的卷积为:
y t = ∑ k = 1 K w k x t − k + 1 y_t = \sum_{k=1}^{K}{w_kx_{t-k+1}} yt=k=1∑Kwkxt−k+1
信号序列x和滤波器w的卷积定义为:
y = w ∗ x \pmb{y} = \pmb{w}* \pmb{x} yyy=www∗xxx
其中 ∗ * ∗表示卷积运算。
特殊的,当 w k = 1 / k , 1 ≤ k ≤ K w_k = 1/ k, 1 \leq k \leq K wk=1/k,1≤k≤K时,卷积相当于信号序列的简单移动平均。
二维卷积
给定一个图像 X ∈ R M × N \pmb{X} \in \mathbb{R}^{M \times N} XXX∈RM×N和滤波器 W ∈ R U × V \pmb{W} \in \mathbb{R}^{U\times V} WWW∈RU×V,其卷积为:
y i j = ∑ u = 1 U ∑ v = 1 V w u v x t − u + 1 , j − v + 1 y_{ij} = \sum_{u=1}^{U} \sum_{v=1}^{V}w_{uv}x_{t-u+1, j-v+1} yij=u=1∑Uv=1∑Vwuvxt−u+1,j−v+1
一个输入信息X和滤波器W的二维卷积定义为:
Y = W ∗ X Y = \pmb{W} * \pmb{X} Y=WWW∗XXX
其中 ∗ * ∗表示卷积运算。二维卷积实例如图:
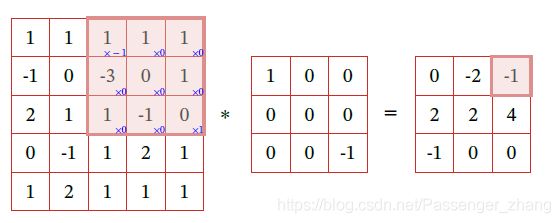
均值滤波为将当前位置的像素设置为滤波器窗口中所有像素的平均值,即 w u v = 1 U V w_{uv} = \frac{1}{UV} wuv=UV1.
卷积常作为特征提取的有效方法,图像经过卷积操作得到的结果叫做特征映射(Feature Map)。以下分别是:高斯滤波器、平滑去噪滤波器、边缘特征提取滤波器。
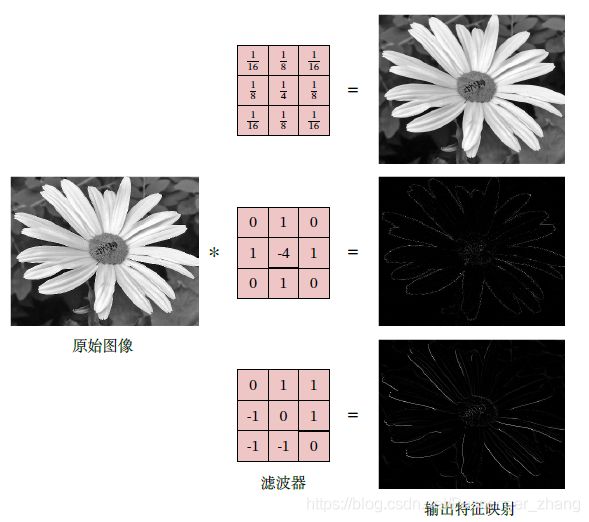
1.1 互相关
在图像处理过程中,计算卷积,需要进行卷积核翻转。在具体实现上,一般使用互相关操作来代替卷积,从而减少开销。互相关是衡量两个序列相关性的函数,使用滑动窗口的点积计算实现,给定一个图像 X ∈ R M × N \pmb{X} \in \mathbb{R}^{M \times N} XXX∈RM×N和卷积核 W ∈ R U × V \pmb{W} \in \mathbb{R}^{U\times V} WWW∈RU×V,它们的互相关为:
y i j = ∑ u = 1 U ∑ v = 1 V w u v x t + u − 1 , j + v − 1 y_{ij} = \sum_{u=1}^{U} \sum_{v=1}^{V}w_{uv}x_{t+u-1, j+v-1} yij=u=1∑Uv=1∑Vwuvxt+u−1,j+v−1
和卷积公式对比:
y i j = ∑ u = 1 U ∑ v = 1 V w u v x t − u + 1 , j − v + 1 y_{ij} = \sum_{u=1}^{U} \sum_{v=1}^{V}w_{uv}x_{t-u+1, j-v+1} yij=u=1∑Uv=1∑Vwuvxt−u+1,j−v+1
互相关和卷积的区别仅仅在于卷积核是否进行翻转。因此互相关也可以称为不翻转卷积。
一个输入信息X和滤波器W的互相关可以定义为:
Y = W ⨂ X = r o t 180 ( W ) ∗ X \begin{aligned} Y & = \pmb{W} \bigotimes \pmb{X} \\ & = rot180(\pmb{W})*\pmb{X} \end{aligned} Y=WWW⨂XXX=rot180(WWW)∗XXX
其中 ⨂ \bigotimes ⨂表示互相关运算, r o t 180 ( ⋅ ) rot180(\cdot) rot180(⋅)表示旋转180度, Y ∈ R M − U + 1 , N − V + 1 \pmb{Y} \in \mathbb{R}^{M-U+1, N-V+1} YYY∈RM−U+1,N−V+1为输出矩阵。
在神经网络中,用卷积进行特征提取,卷积核翻转不影响其特征提取能力,当卷积核为可学习参数时,卷积核互相关在能力上等价,故常用互相关来代替卷积(绝大部分深度学习工具亦如此)。
在后续的文章中,用互相关代替卷积,即本文中的卷积符号用 ⨂ \bigotimes ⨂表示,而真正的卷积用 ∗ * ∗表示。
1.2 卷积的变种
引入滑动步长和零填充增加卷积多样性。滑动步长 (Stride)是指滤波器在滑动时的时间间隔。零填充(Zero Padding)是在输入向量的边界外进行补零。示意图如下:
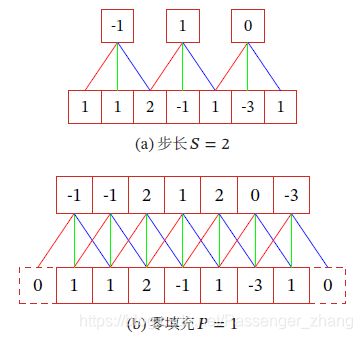
1.2.1 转置卷积
常见的卷积是进行降维操作,但一些卷积也可以将低维特征映射到高维特征。
对于高维向量 x ∈ R d \pmb{x} \in \mathbb{R}^{d} xxx∈Rd和低维向量 z ∈ R p \pmb{z} \in \mathbb{R}^{p} zzz∈Rp, p < d p < d p<d。方式变换 W ∈ R p × d \pmb{W} \in \mathbb{R}^{p \times d} WWW∈Rp×d将高维映射到低维:
z = W x \pmb{z} = \pmb{Wx} zzz=WxWxWx
通过转置 W \pmb{W} WWW实现低维到高维反向映射:
x = W T z \pmb{x} = \pmb{W^{T}z} xxx=WTzWTzWTz
卷积操作可以写成仿射变换方式。假设一个5 维向量 x \pmb{x} xxx,经过大小为3 的卷积核 w = [ w 1 , w 2 , w 3 ] T \pmb{w} = [w_1, w_2, w_3]^{T} www=[w1,w2,w3]T 进行卷积,得到3 维向量 z \pmb{z} zzz。卷积操作可以写为:

其中 C \pmb{C} CCC是一个稀疏矩阵,其非零元素来自于卷积核 w \pmb{w} www中的元素。
要实现3 维向量 z \pmb{z} zzz到5 维向量 x \pmb{x} xxx的映射,可以通过仿射矩阵的转置来实现:
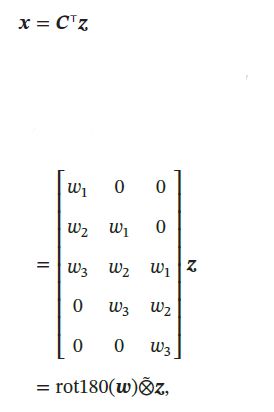
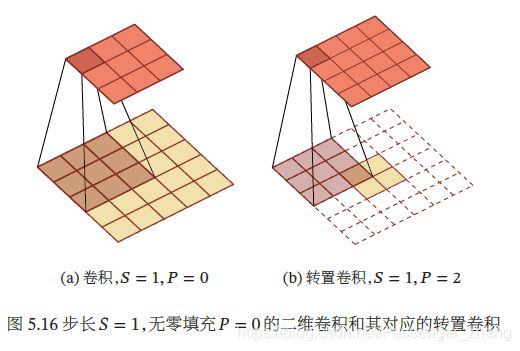
将低维特征映射到高维特征的卷积操作称为转置卷积(Transposed Convolution)也称为反卷积(Deconvolution)。步长 = 1,无零填充 = 0 的二维卷积和其对应的转置卷积:
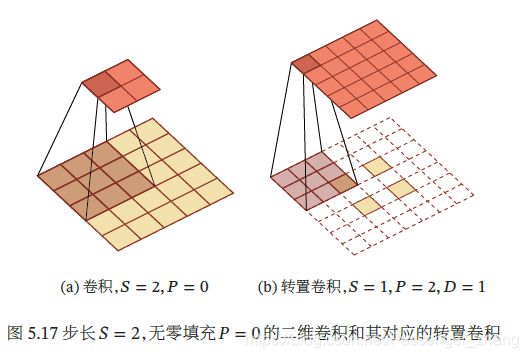
微步卷积 通过减少转置卷积的步长 < 1来实现上采样操作,大幅提高特征维数。步长 < 1 的转置卷积也称为微步卷积。为了实现微步卷积,可以在输入特征之间插入0 来间接地使得步长变小。如果卷积操作的步长为 > 1,希望其对应的转置卷积的步长为 1 S \frac{1}{S} S1 。需要在输入特征之间插入 − 1 个0 来使得其移动的速度变慢。步长 = 2,无零填充 = 0 的二维卷积和其对应的转置卷积如图:
1.2.2 空洞卷积
对于卷积层想增加输出单元的感受野可以:
(1)增加卷积核大小(但会增加参数量)
(2)增加卷积的层数(但会增加参数量)
(3)卷积之前进行汇聚操作(但会丢失信息)
(4)空洞卷积(不增加参数量)
空洞卷积又称膨胀卷积,通过给卷积核插入空洞来增加大小,如果在卷积核每两元素之间插入 D − 1 D-1 D−1 个空洞,卷积核的有效大小为:

D为膨胀率,当D=1时,卷积核为普通的卷积核。

转置卷积、空洞卷积动态实例:转置卷积空洞卷积动态图
1.3 卷积的数学性质
1.3.1 交换性
如不限制卷积信号长度,翻转卷积具有交换性,即 x ∗ y = y ∗ x \pmb{x} * \pmb{y} = \pmb{y} * \pmb{x} xxx∗yyy=yyy∗xxx。互相关“卷积”,同样具有交换性。
宽卷积 给定图像 X ∈ R M × N \pmb{X} \in \mathbb{R}^{M \times N} XXX∈RM×N和卷积核 W ∈ R U × V \pmb{W} \in \mathbb{R}^{U\times V} WWW∈RU×V,对图像进行零填充,两端各补 U − 1 U-1 U−1和 V − 1 V-1 V−1个零,得到全填充(Full Padding)图像 X ^ ∈ R ( M + 2 U − 2 ) × ( N + 2 V − 2 ) \pmb{\hat{X}} \in \mathbb{R}^{(M+2U-2) \times (N+2V-2)} X^X^X^∈R(M+2U−2)×(N+2V−2)。宽卷积的定义:
W ⨂ ^ X ≜ W ⨂ ^ X ^ \pmb{W} \hat{\bigotimes} \pmb{X} \triangleq \pmb{W} \hat{\bigotimes} \pmb{\hat{X}} WWW⨂^XXX≜WWW⨂^X^X^X^
其中 ⨂ ^ \hat{\bigotimes} ⨂^表示宽卷积运算。
当输入信息和卷积核具有固定长度时,其宽卷积仍具有交换性:
r o t 180 ( W ) ⨂ ^ X = r o t 180 ( X ) ⨂ ^ W 。 rot180(\pmb{W}) \hat{\bigotimes} \pmb{X} = rot180(\pmb{X}) \hat{\bigotimes} \pmb{W}。 rot180(WWW)⨂^XXX=rot180(XXX)⨂^WWW。
1.3.2 导数
假设 Y = W ⨂ X Y = \pmb{W} \bigotimes \pmb{X} Y=WWW⨂XXX,其中 X ∈ R M × N \pmb{X} \in \mathbb{R}^{M \times N} XXX∈RM×N, W ∈ R U × V \pmb{W} \in \mathbb{R}^{U \times V} WWW∈RU×V, Y ∈ R ( M − U + 1 ) × ( N − V + 1 ) \pmb{Y} \in \mathbb{R}^{(M-U+1) \times (N-V+1)} YYY∈R(M−U+1)×(N−V+1),函数 f ( Y ) ∈ R f(Y) \in \mathbb{R} f(Y)∈R 是一个标量函数,则:
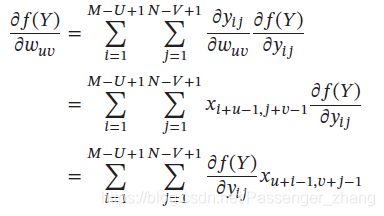
从最后一个公式可看出:
∂ f ( Y ) ∂ W = ∂ f ( Y ) ∂ Y ⨂ X \frac{\partial{f(Y)}}{\partial{\pmb{W}}} = \frac{\partial{f(Y)}}{\partial{\pmb{Y}}} \bigotimes \pmb{X} ∂WWW∂f(Y)=∂YYY∂f(Y)⨂XXX
同理:
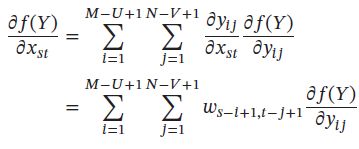
其中当 ( s − i + 1 ) < 1 (s - i + 1) < 1 (s−i+1)<1,或 ( s − i + 1 ) > U (s - i + 1) > U (s−i+1)>U,或 ( t − j + 1 ) < 1 (t - j + 1) < 1 (t−j+1)<1,或 ( t − j + 1 ) > V (t - j + 1) > V (t−j+1)>V时, w s − i + 1 , i − j + 1 = 0 w_{s-i+1, i-j+1} = 0 ws−i+1,i−j+1=0。即相当于对 W 进行了 P = ( M − U , N − V ) P = (M - U, N - V) P=(M−U,N−V)的零填充。
使用互相关的“卷积”:
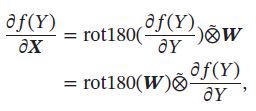
2. 卷积神经网络
CNN一般由卷积层、汇聚层、全连接层构成。
2.1 用卷积代替全连接
两个原因:
局部连接 在卷积层中(第 l l l 层)每一个神经元只和下一层(第 l − 1 l-1 l−1 层)中某个局部窗口内的神经元连接,构成局部连接网络,卷积层和下一层连接数大大减少,由 M l × M l − 1 M_l \times M_{l-1} Ml×Ml−1 个连接变为 M l × K M_l \times K Ml×K 个连接,K为滤波器大小。

权重共享 一个滤波器只捕捉输入数据的一种特定的局部特征。因此提取多个特征就要多个不同的滤波器。滤波器 w ( l ) \pmb{w}^{(l)} www(l) 对于第 l l l 层的所有的神经元都是相同的,如上图(b),同颜色上的连接权重相同。
由于局部连接和权重共享的存在,卷积层的参数个数与神经元的数量无关,卷积层的参数只有K维权重 w ( l ) \pmb{w}^{(l)} www(l) 和 l l l 维的偏置 b ( l ) b^{(l)} b(l),共 K+1 个参数。
2.2 卷积层
不同的卷积核相当于不同的特征提取器。
为充分利用图像的局部信息,经常将神经元组织为三维结构的神经层,大小为 M * N * D ,由 D 个 M * N 大小的特征映射构成。为提高卷积网络的表示能力,可以在每一层使用多个不同的特征映射。
在输入层:特征映射是图像本身。
灰度图像:有一个特征映射,输入层深度D=1。
彩色图像:有RGB三个颜色通道的特征映射,输入层深度D=3。
卷积层的结构:
(1)输入特征映射组: X ∈ R M × N × D \pmb{X} \in \mathbb{R}^{M \times N \times D} XXX∈RM×N×D 为三维张量(tensor),每个切片(Slice)矩阵 X d ∈ R M × N \pmb{X}^{d} \in \mathbb{R}^{M \times N} XXXd∈RM×N 为一个输入特征映射, 1 ≤ d ≤ D 1 \leq d \leq D 1≤d≤D;
(2)输出特征映射组: Y ∈ R M ′ × N ′ × P \pmb{Y} \in \mathbb{R}^{M^{'} \times N^{'} \times P} YYY∈RM′×N′×P 为三维张量,每个切片矩阵 Y p ∈ R M ′ × N ′ \pmb{Y}^{p} \in \mathbb{R}^{M^{'} \times N^{'}} YYYp∈RM′×N′ 为一个输出特征映射, 1 ≤ p ≤ P 1 \leq p \leq P 1≤p≤P;
(3)卷积核: W ∈ R U × V × D × P \pmb{W} \in \mathbb{R}^{U \times V \times D \times P} WWW∈RU×V×D×P 为四维张量,每个切片矩阵 W p , d ∈ R U × V \pmb{W}^{p,d} \in \mathbb{R}^{U \times V} WWWp,d∈RU×V 为一个二维卷积核, 1 ≤ d ≤ D , 1 ≤ p ≤ P 1 \leq d \leq D, 1 \leq p \leq P 1≤d≤D,1≤p≤P;
卷积层的三维结构如图:
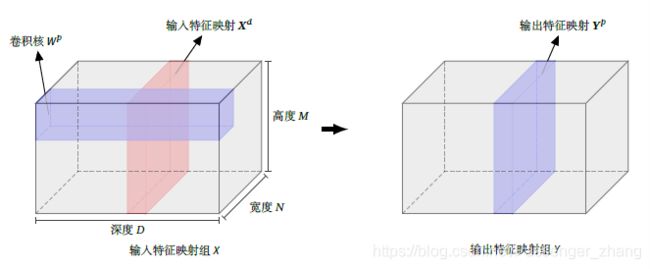
输出特征映射 Y p Y^p Yp 的计算:

其中 W p ∈ R U × V × D \pmb{W}^p \in \mathbb{R}^{U \times V \times D} WWWp∈RU×V×D 为三维卷积核, f ( ⋅ ) f(\cdot) f(⋅) 常为ReLU的非线性激活函数。如希望卷积层输出P个特征映射,可将该计算过程重复P次:

在输入为 X ∈ R M × N × D \pmb{X} \in \mathbb{R}^{M \times N \times D} XXX∈RM×N×D ,输出为 Y ∈ R M ′ × N ′ × P \pmb{Y} \in \mathbb{R}^{M^{'} \times N^{'} \times P} YYY∈RM′×N′×P 的卷积层中,每一个输出特征映射需要D个滤波器以及一个偏置b。假设每个滤波器的大小为 U × V U \times V U×V, 那么共需 P × D × ( U × V ) + P P \times D \times (U \times V) + P P×D×(U×V)+P个参数。
2.3 汇聚层(池化层)
汇聚层(Pooling Layer) 也叫子采样层(Subsampling Layer),作用是特征选择,降维。因为卷积层只减少了网络中连接的数量,却没有减少特征映射组中的神经元个数。
汇聚层的输入特征映射组为 X ∈ R M × N × D \pmb{X} \in \mathbb{R}^{M \times N \times D} XXX∈RM×N×D ,对于其中的每一个映射组 X d ∈ R M × N \pmb{X}^d \in \mathbb{R}^{M \times N} XXXd∈RM×N, 1 ≤ d ≤ D 1 \leq d \leq D 1≤d≤D,将其分为多个可重叠的区域 R m , n d R_{m,n}^d Rm,nd , 1 ≤ m ≤ M ′ 1 \leq m \leq M^{'} 1≤m≤M′, 1 ≤ n ≤ N ′ 1 \leq n \leq N^{'} 1≤n≤N′。汇聚层对每个区域进行下采样(Down Sampling)得到一个值,作为这个区域的概括。常见的两个汇聚函数:
(1)最大汇聚(Max Pooling):
y m , n d = max i ∈ R m , n d x i y_{m,n}^{d} = \max_{i \in R_{m,n}^{d}} x_i ym,nd=i∈Rm,ndmaxxi
其中 x i x_i xi 为 区域 R k d R_k^d Rkd 内每个神经元的活性值。
(2)平均汇聚(Mean Pooling):
y m , n d = 1 ∣ R m , n d ∣ ∑ i ∈ R m , n d x i y_{m,n}^{d} = \frac{1}{|R_{m,n}^d|} \sum_{i \in R_{m,n}^{d}} x_i ym,nd=∣Rm,nd∣1i∈Rm,nd∑xi
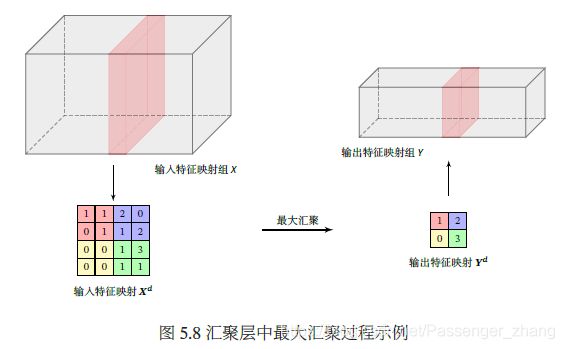
汇聚层既可以减少神经元数量,又可以是网络对一些相对小的局部形态改变保持不变性,并拥有更大的感受野。
目前主流的卷积网络中,汇聚层仅含下采样操作,早期卷积网络(LeNet-5) 中,会在汇聚层后接激活函数。
典型的汇聚层为对 2 ∗ 2 2 * 2 2∗2 的不重叠区域记性最大汇聚。汇聚层可以看做特殊的卷积层,卷积核大小为 K ∗ K K * K K∗K ,步长为 S ∗ S S * S S∗S,卷积核为max函数 或 mean函数。过大的采样区域会急剧减少神经元的数量,也会造成过多的信息损失。
2.4 典型的卷积网络结构
典型的卷积网络结构如图:

一个卷积块为连续M个卷积层和b个汇聚层(M常为2-5,b常为0或1)。一个卷积网络中可以堆叠 个连续的卷积块,然后在后面接 K 个全连接层(N常为1-100,b常为0-2)。
目前,网络结构趋向于更小的卷积核(11或33)、更深的结构(大于50层)。此外,由于卷积的操作性越来越灵活(不同的步长),汇聚层作用渐小,故目前流行的卷积网络中汇聚层在减少,趋向于全卷积网络。
3 参数学习
利用误差反向传播算法进行参数学习。
设第 l l l 层为卷积层,第 l − 1 l-1 l−1 层的输入特征映射为 X ( l − 1 ) ∈ R M × N × D X^{(l-1)} \in \mathbb{R}^{M \times N \times D} X(l−1)∈RM×N×D,通过卷积计算得到第 l l l层的特征映射净输入 Z ( l ) ∈ R M ′ × N ′ × P Z^{(l)} \in \mathbb{R}^{M^{'} \times N^{'} \times P} Z(l)∈RM′×N′×P。第 l l l层的第 p p p个特征映射净输入:
Z ( l , p ) = ∑ d = 1 D W ( l , p , d ) ⨂ X ( l − 1 , d ) + b ( l , p ) Z^{(l,p)} = \sum_{d=1}^{D} \pmb{W}^{(l,p,d)} \bigotimes \pmb{X}^{(l-1,d)} + b^{(l,p)} Z(l,p)=d=1∑DWWW(l,p,d)⨂XXX(l−1,d)+b(l,p)
其中 W ( l , p , d ) \pmb{W}^{(l,p,d)} WWW(l,p,d) 和 b ( l , p ) b^{(l,p)} b(l,p) 为卷积核以及偏置。第 l l l层中共有 P × D P \times D P×D个卷积核和 P P P个偏置,可用链式法则求导。
损失函数 L L L 关于第 l l l 层的卷积核 W ( l , p , d ) \pmb{W}^{(l,p,d)} WWW(l,p,d) 的偏导:

其中
δ ( l , p ) = ∂ L ∂ Z ( l , p ) \delta^{(l,p)} = \frac{\partial L}{\partial Z^{(l,p)}} δ(l,p)=∂Z(l,p)∂L 为损失函数关于第 l l l 层的第 p p p个特征映射净输入 Z ( l , p ) Z^{(l,p)} Z(l,p)的偏导数;
∂ L ∂ b ( l , p ) = ∑ i , j [ δ ( l , p ) ] i , j \frac{\partial L}{\partial b^{(l,p)}} = \sum_{i,j}[\delta^{(l,p)}]_{i,j} ∂b(l,p)∂L=∑i,j[δ(l,p)]i,j为损失函数关于第 l l l层的第p个偏置 b ( l , p ) b^{(l,p)} b(l,p)的偏导数。
在卷积网络中,每层参数的梯度依赖于其所在层的误差项 δ ( l , p ) \delta^{(l,p)} δ(l,p)。
3.1 误差项的计算
误差项 δ ( l , p ) \delta^{(l,p)} δ(l,p)的计算是关键。
汇聚层 当第 l + 1 l+1 l+1 层为汇聚层时,因汇聚层时下采样, l + 1 l+1 l+1 层的每个神经元的误差项 δ \delta δ 对应于第 l l l 层的相应特征映射的一个区域, l l l 层的第 p p p 个特征映射中的每个神经元都有一条边和 l + 1 l+1 l+1 层的第 p p p 个特征映射中的一个神经元相连. 根据链式法则,第 l l l 层的一个特征映射的误差项 δ ( l , p ) \delta^{(l,p)} δ(l,p),只需要将 l + 1 l+1 l+1 层对应特征映射的误差项 δ ( l + 1 , p ) \delta^{(l+1,p)} δ(l+1,p) 进行上采样操作(和第 l l l 层的大小一样),再和 层特征映射的激活值偏导数逐元素相乘,就得到了 δ ( l , p ) \delta^{(l,p)} δ(l,p)。

其中 f l ′ ( ⋅ ) f_l^{'}(\cdot) fl′(⋅)为第 l l l层使用的激活函数的导数,up为上采样函数。若下采样是最大汇聚,误差项 δ ( l + 1 , p ) \delta^{(l+1,p)} δ(l+1,p) 中的每个值都直接传到上一层对应区域中的最大值所对应的神经元,该区域其他神经元的误差项设为0。若下采样是平均汇聚,误差项 δ ( l + 1 , p ) \delta^{(l+1,p)} δ(l+1,p) 中的每个值都会被平均分配到上一层对应区域中的所有神经元上。
卷积层当 l + 1 l+1 l+1 层为卷积层时,假设特征映射净输入 Z ( l + 1 ) ∈ R M ′ × N ′ × P Z^{(l+1)} \in \mathbb{R}^{M^{'} \times N^{'} \times P} Z(l+1)∈RM′×N′×P。其中第 p ( 1 ≤ p ≤ P ) p(1 \leq p \leq P) p(1≤p≤P) 个特征映射输入为:
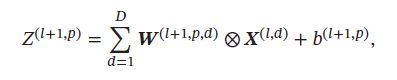
其中 W ( l + 1 , p , d ) \pmb{W}^{(l+1, p, d)} WWW(l+1,p,d) 和 b ( l + 1 , p ) b^{(l+1, p)} b(l+1,p) 为第 l + 1 l+1 l+1 层的卷积核、偏置。第 l + 1 l+1 l+1 层中共有 P × D P \times D P×D 个卷积核和 P P P 个偏置。第 l l l 层的第 d d d 个特征映射的误差项 δ ( l , d ) \delta^{(l,d)} δ(l,d) 的具体推导过程如下,其中 ⨂ ^ \hat{\bigotimes} ⨂^ 为宽卷积:
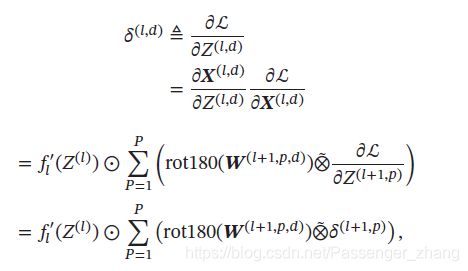
4 典型的卷积神经网络
4.1 LeNet-5
LeNet-5网络结构如图:
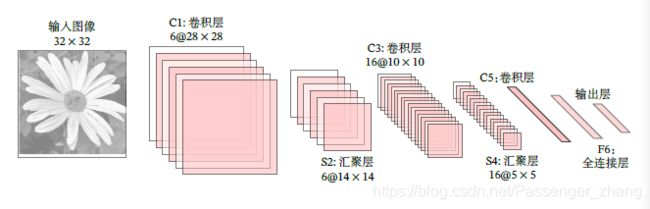
LeNet-5网络共有7层,输入图像为 32 × \times × 32,输出对应为10个类别数字的概率得分。每层结构如下:
- C1卷积层:6个5 × \times × 5的滤波器,得到6组28 × \times × 28=784的特征映射,故C1层的神经元数量为6 × \times × 784=4704,可训练参数数量为6 × \times × 25+6=156,连接数为156 × \times × 784=122304.
- S2汇聚层:平均汇聚,采样窗口为 2 × \times × 2,并接一个激活函数,神经元个数为6 × \times × 14 × \times × 14 = 1176,可训练参数数量为 6 × ( 1 + 1 ) = 12 6 \times (1+1) = 12 6×(1+1)=12,连接数为 6 × 196 × ( 4 + 1 ) = 5880 6 \times 196 \times (4+1) = 5880 6×196×(4+1)=5880。
- C3卷积层:LeNet-5用连接表来定义输入和输出特征映射之间的依赖关系,共使用60个 5 × 5 5 \times 5 5×5 的滤波器,得到16组大小为 10 × 10 10 \times 10 10×10 的特征映射,神经元个数为16 × \times × 100 = 1600,可训练参数数量为 60 × 25 + 1 = 1516 60 \times 25 + 1 = 1516 60×25+1=1516,连接数为 100 × 1516 = 151600 100 \times 1516 = 151600 100×1516=151600。
- S4汇聚层:采样窗口为 2 × 2 2 \times 2 2×2 ,得到16个 5 × 5 5 \times 5 5×5大小的特征映射,可训练参数数量为 16 × 2 = 32 16 \times 2 = 32 16×2=32,连接数为 16 × 25 × ( 4 + 1 ) = 2000 16 \times 25 \times (4+1) = 2000 16×25×(4+1)=2000。
- C5卷积层:使用 120 × 16 = 1920 120 \times 16 = 1920 120×16=1920 个 5 × 5 5 \times 5 5×5 的滤波器,得到120组大小为 1 × 1 1 \times 1 1×1 的特征映射。C5层的神经元数量为120,可训练参数数量为 1920 × 25 + 120 = 48120 1920 \times 25 + 120 = 48120 1920×25+120=48120,连接数为 120 × ( 16 × 25 + 1 ) = 48120 120 \times (16 \times 25 + 1) = 48120 120×(16×25+1)=48120。
- F6全连接层:84个神经元,可训练参数数量为 84 × ( 120 + 1 ) = 10164 84 \times (120+1) = 10164 84×(120+1)=10164。连接数和可训练参数个数相同,为10164。
- 输出层:输出层由 10个径向基函数 组成。
连接表 卷积层的输入和输出特征映射之间是全连接关系,可用连接表转为为非全连接关系。

C3层的第0-5个特征映射依赖于S2 层的特征映射组的每3个连续子集,第6-11个特征映射依赖于S2 层的特征映射组的每4个连续子集,第12-14个特征映射依赖于S2 层的特征映射的每4个不连续子集,第15个特征映射依赖于S2 层的所有特征映射。
如果第p个输出特征映射依赖于第个输入特征映射,则 T p , d = 1 T_{p,d} = 1 Tp,d=1,否则为0。

其中 为 × 大小的连接表. 假设连接表 的非零个数为,每个滤波器的大小为 × ,那么共需要 × × + 参数。
4.2 AlexNet
AlexNet是第一个现代深度卷积网络模型,首次使用GPU 进行并行训练,采用了ReLU 作为非线性激活函数,使用Dropout 防止过拟合,使用数据增强来提高模型准确率等。AlexNet 赢得了2012 年ImageNet 图像分类竞赛的冠军。
AlexNet网络规模超出了当时的单个GPU 的内存限制,AlexNet 将网络拆为两半,分别放在两个GPU 上,GPU 间只在某些层(比如第3层)进行通信。

AlexNet 的输入为224 × 224 × 3 的图像,输出为1 000 个类别的条件概率,具体结构如下:
- 卷积层1:两个大小为11 × 11 × 3 × 48 的卷积核,步长 = 4,零填充 = 3,得到两个大小为55 × 55 × 48 的特征映射组。
- 汇聚层1:为3 × 3 的最大汇聚操作,步长 = 2,得到两个27 × 27 × 48 的特征映射组。
- 卷积层2:两个大小为5 × 5 × 48 × 128 的卷积核,步长 = 1,零填充 = 2,得到两个大小为27 × 27 × 128 的特征映射组。
- 汇聚层2:3 × 3 的最大汇聚操作,步长 = 2,得到两个大小为13 × 13 × 128 的特征映射组。
- 卷积层3:两个路径的融合,使用一个大小为3 × 3 × 256 × 384 的卷积核,步长 = 1,零填充 = 1,得到两个大小为13 × 13 × 192 的特征映射组。
- 卷积层4:两个大小为3 × 3 × 192 × 192 的卷积核,步长 = 1,零填充 = 1,得到两个大小为13 × 13 × 192 的特征映射组。
- 卷积层5:两个大小为3 × 3 × 192 × 128 的卷积核,步长 = 1,零填充 = 1,得到两个大小为13 × 13 × 128 的特征映射组。
- 汇聚层3:3 × 3 的最大汇聚操作,步长 = 2,得到两个大小为6 × 6 × 128 的特征映射组。
- 全连接层:三个全连接层,神经元数量分别为4096、4096 和1 000。
AlexNet 在前2个汇聚层之后进行了局部响应归一化(Local Response Normalization,LRN)以增强模型的泛化能力。
4.3 Inception
在Inception 网络中,一个卷积层包含多个不同大小的卷积操作,称为Inception 模块。Inception 网络是由有多个Inception 模块和少量的汇聚层堆叠而成。
Inception 模块同时使用1 × 1、3 × 3、5 × 5 等不同大小的卷积核,并将得到的特征映射在深度上拼接(堆叠)起来作为输出特征映射。先用1 × 1卷积对四组平的特征抽取方式进行减少特征映射的深度。

Inception V1版本的GoogleNet是2014 年ImageNet 图像分类竞赛的冠军。由9个Inception V1模块和5个汇聚层、卷积层、全连接层共22层网络构成,并引入两个辅助分类器来加强监督信息以解决梯度消失问题:
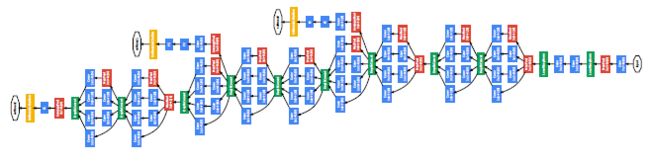
高清图见:GoogLeNet网络结构图
Inception 网络有多个改进版本,如Inception V3:Inception v3 网络用多层的小卷积核来替换大的卷积核,以减少计算量和参数量,并保持感受野不变。具体包括:(1)使用两层3 × 3 的卷积来替换v1 中的5 × 5 的卷积;(2)使用连续的 × 1 和1 × 来替换 × 的卷积。引入了标签平滑以及批量归一化等优化方法进行训练。
4.4 残差网络
残差网络(Residual Network,ResNet)通过给非线性的卷积层增加直连边(Shortcut Connection)提高信息的传播效率。
在一个深度网络中,常用一个非线性单元 f ( x ; θ ) f(\pmb{x};\theta) f(xxx;θ) 去逼近目标函数 h ( x ) h(x) h(x) 。若将目标函数拆分为:恒等函数 x \pmb{x} xxx 和残差函数 h ( x ) − x h(\pmb{x}) - \pmb{x} h(xxx)−xxx:

残差函数更容易学习,故将优化问题转为:让非线性单元 f ( x ; θ ) f(\pmb{x};\theta) f(xxx;θ) 去逼近残差函数 h ( x ) − x h(\pmb{x}) - \pmb{x} h(xxx)−xxx,利用 f ( x ; θ ) + x f(\pmb{x};\theta) + \pmb{x} f(xxx;θ)+xxx 去逼近 h ( x ) h(\pmb{x}) h(xxx)。
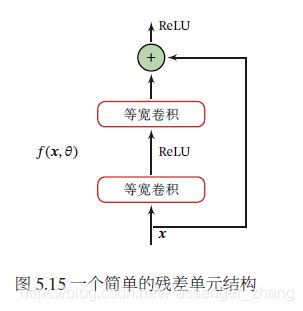
残差网络将很多个残差单元串联起来构成的一个非常深的网络。残差单元由多个级联的(等宽)卷积层和一个跨层的直连边组成,再经过ReLU 激活后得到输出: