背包问题汇总

背包问题

背包问题一直是动态规划算法中的经典系列，下面我将常见的所有背包问题进行总结分析

0 1 背包问题

关键理解背包的推到公式：fn[i][j]代表在此时此刻拥有j体积下前i个物品中最优的选择价值为多少，那么具体的决策是 如果体积不够装当前的物品，那么f[i][j]=f[i-1][j],如果体积可以装下当前的物品，那么我们判断是不装入得到最优价值还是装入得到最优的价值 f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]]+w[i]);根据题目给出的输入样例，我们画表格手动推到一下就更加理解公式的含义

二维数组代码如下

#include
#include
using namespace std;
const int N=1e3+10;
int v[N],w[N];
int fn[N][N];

int main()
{
    int x,y;
    cin>>x>>y;
    for(int i=1;i<=x;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=x;i++)
    {
        for(int j=1;j<=y;j++)
        {
            fn[i][j]=fn[i-1][j];
            if(j>=v[i])
            {
                fn[i][j]=max(fn[i][j],fn[i-1][j-v[i]]+w[i]);
            }
        }
    }
        int ans=0;
    for(int i=1;i<=y;i++)ans=max(ans,fn[x][i]);
    cout<<ans;
    return 0;
}

优化过的一维数组代码如下（一定要手动画表格推一下）

#include
#include
using namespace std;
const int N=1e3+10;
int v[N],w[N];
int f[N];
int main()
{
    int x,y;
    cin>>x>>y;
    for(int i=1;i<=x;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=x;i++)
    {
        for(int j=y;j>=1;j--)
        {
            if(j>=v[i])
            {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            }
        }
    }
    int ans=0;
    for(int i=1;i<=y;i++)ans=max(ans,f[i]);
    cout<<ans;
    return 0;
}

完全背包问题

完全背包是在0 1背包 基础上进一步推到而成的，推到步骤十分简单，但需要理解之间的含义

完全背包问题和0 1 背包问题区别在于商品的个数，暴力做法我们只需要在01背包的两层循环加入第三层循环商品个数即可，但考虑时间复杂度问题我们必须通过公式推导出之间的联系，下面进行公式推到


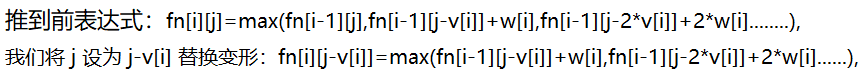
二维数组代码

#include
#include
using namespace std;
const int N=1e3+10;
int v[N],w[N];
int f[N][N];
int main()
{
    int x,y;
    cin>>x>>y;
    for(int i=1;i<=x;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=x;i++)
    {
        for(int j=1;j<=y;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])
            {
                f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
            }
        }
    }
    int ans=0;
    for(int i=1;i<=y;i++)ans=max(ans,f[x][i]);
    cout<<ans;
    return 0;
}

一维数组代码

#include
#include
using namespace std;
const int N=1e3+10;
int v[N],w[N];
int f[N];
int main()
{
    int x,y;
    cin>>x>>y;
    for(int i=1;i<=x;i++)
    {
        cin>>v[i]>>w[i];
    }
    for(int i=1;i<=x;i++)
    {
        for(int j=1;j<=y;j++)
        {
            f[j]=f[j];
            if(j>=v[i])
            {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            }
        }
    }
    int ans=0;
    for(int i=1;i<=y;i++)ans=max(ans,f[i]);
    cout<<ans;
    return 0;
}

多重背包问题
多重背包问题 同样由 0 1背包问题衍生而来 多重背包严格限制了物品的数量，因此我们在0 1背包代码的基础上 多循环一层物品的数量即可 若理解0 1 背包一维数组的含义 那么多重背包代码就十分简单

#include
#include
#include
#include
using namespace std;
const int N=110;
int v[N],w[N],s[N];
int dp[N][N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i]>>s[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            for(int k=1;k<=s[i];k++)
            {
                dp[i][j]=max(dp[i-1][j],dp[i][j]);
                if(j>=k*v[i])
                {
                    dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
                }
            }
    cout<<dp[n][m];
    return 0;
}

以内，因此下面对代码进行推导优化
其实我们可以把多重背包当成0 1 背包问题去思考，把有限个数的物品全部拆成数量为一的物品，那么就转化为了0 1背包问题，但是我们要进一步思考，全拆成数量为一的物品一定是最笨最耗时的拆分。举个例子，假如数量为10的物品，我们拆成
1 2 4 8 2 五种物品，那么无论怎么组合 一定可以组合1~10的任意数量的此物品

#include
#include
#include
#include
using namespace std;
const int N=21000;
int v[1010],w[1010],s[1010];
struct SUM
{
    int v,w,s;
}sum[N];
long long int dp[2010];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i]>>s[i];
    int cmt=1;
    for(int i=1;i<=n;i++)//拆分并添加进结构体
    {
        for(int k=1;;k=k*2)
        {
            if(s[i]>=k)
            {
                s[i]-=k;
                sum[cmt].v=v[i];
                sum[cmt].w=w[i];
                sum[cmt++].s=k;
            }
            else if(s[i]!=0)
            {
                sum[cmt].v=v[i];
                sum[cmt].w=w[i];
                sum[cmt++].s=s[i];
                s[i]=0;
            }
            else break;
        }
    }
    for(int i=1;i<cmt;i++)//0 1背包一维数组优化
        for(int j=m;j>=sum[i].v*sum[i].s;j--)
        {
            dp[j]=max(dp[j],dp[j-sum[i].v*sum[i].s]+sum[i].s*sum[i].w);
        }
   long long int ans=0;
   for(int i=1;i<=m;i++)
        ans=max(ans,dp[i]);
    cout<<ans;
    return 0;
}

分组背包问题

分组背包特别注意循环体积大小和循环组内物品的顺序是固定的，不能颠倒，因为组内物品的体积并不是按从小到大排序的

#include
#include
using namespace std;
const int N=110;
int v[N],w[N],dp[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int s;
        cin>>s;
        for(int j=1;j<=s;j++)
            cin>>v[j]>>w[j];
        for(int kk=m;kk>=1;kk--)
            for(int k=1;k<=s;k++)
            {   
                if(kk>=v[k])
                    dp[kk]=max(dp[kk],dp[kk-v[k]]+w[k]);
            }
    }
    cout<<dp[m];
    return 0;
}