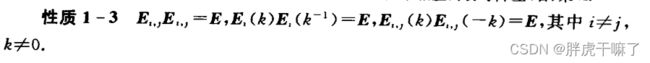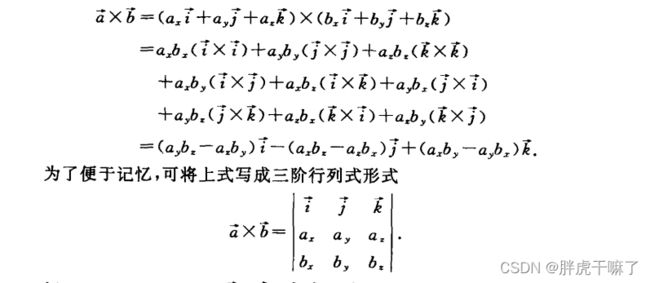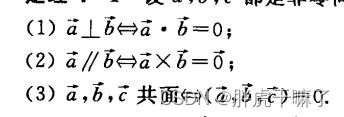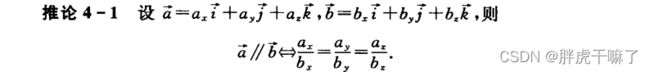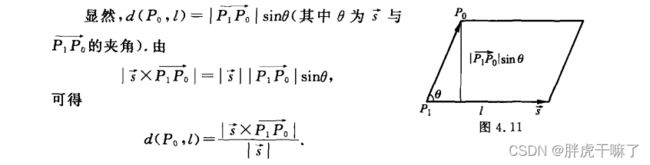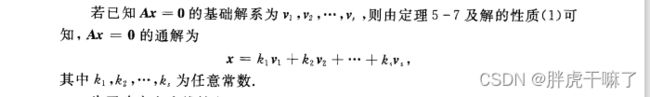线性代数复习

线性代数复习——定义、定理、推论汇总

本博客主要根据教材《线性代数与解析几何》，代万基编写，对课本上概念等进行简单罗列，融合了一些个人理解，以供复习。

第1章 矩阵及其初等变换

本章内容：矩阵及其运算，向量与分块矩阵，矩阵的初等变换与初等矩阵。

1.1 矩阵及其运算

1.1.1 矩阵的概念

定义1-1：由mxn个数a_ij（i1,2,…,m;j=1,2,3,…n）所排成的m行n列的矩形鼠标成为mxn矩阵。

• 只有一行的矩阵称为行矩阵，记作[a1,a2,…,an]；
• 只有一列的矩阵称为列矩阵，记作[a1,a2,…an]^T。
• nxn矩阵A=[a_ij]_nxn一般称为n阶矩阵或n阶方阵。方阵中自左上角至右下角的连线叫做A的主对角线，自右上角至左下角的连线叫做A的副对角线，位于主对角线上的元素a11,a22,…,ann叫做A的对角元。
• 三角形矩阵：分三类，对角阵、上三角形矩阵和下三角形矩阵。对角矩阵可记为diag(a11,a22,…,ann)。
• 对角元都为1的对角矩阵叫做单位矩阵，用E或者I表示。
• 若矩阵A和B的行数和列数均相同，则称矩阵A和B为同型矩阵
• 若矩阵A和B 为同型矩阵，并且听他们对应的元素都相等，则称矩阵A和B相等，记作A=B。
• 元素都是示数的矩阵叫做实矩阵，元素是复数的矩阵叫做复矩阵。

1.1.2 矩阵的线性运算

定义1-2：设A=[aij]_mxn,B=[bij]_mxn，规定矩阵A与B的和为A+B=[aij+bij]_mxn，即两个矩阵的加法就是将他们的对应元素相加

• note：两个矩阵进行加法或减法运算的前提是，矩阵同型。
  定义1-3：数k与矩阵A=[a_ij]_mxn的乘积规定为kA=Ak=[ka_ij]_mxn，即数k与矩阵A相乘就是把数k与矩阵A的每个元素相乘
• 矩阵的加法和数与与矩阵的乘法这两种运算统称为矩阵的线性运算。
• 矩阵的线性运算的八条性质：
  （1）A+B=B+A        （矩阵间的加法交换律）
  （2）(A+B)+C= A+(B+C)   （矩阵间的加法结合律）
  （3）A+O=A        （矩阵对0的加法）
  （4）A+(-A)=O       （矩阵和其负矩阵的加和为O）
  （5）1A=A         （矩阵与1）
  （6）k(tA)=(kt)A       （矩阵和数间的结合律）
  （7）(k+t)A = kA+tA     （数对矩阵的的分配律）
  （8）k(A+B)= kA+kB     （矩阵对数的分配律）

1.1.3 矩阵的乘法

定义1-4：设A=[a_ij]_mxk，B=[b_ij]_kxn，规定矩阵A和B的成绩是一个mxn矩阵C=[c_ij]_mxn，其中c_ij=a_i1b_1j+a_i2b_2j+…+a_ikb_kj=$$\sum _{l=1}^k{a}_{il}{b}_{lj}$$记作AB=C

• 只有当矩阵A的列数等于矩阵B的行数时，才能够做乘法运算AB
• 矩阵乘法与数的乘法不同的是：

（1）矩阵的乘法不满足交换律，即一般AB不等于BA，原因有三：
i)AB可相乘不代表BA可相乘
ii)当AB和BA都可以相乘时，其结果的类型不一定相同
iii)当AB和BA的类型相同时，其对应的元素不一定相同

（2）矩阵的乘法不满足消去律。

• 当矩阵A和B满足AB=BA时，称矩阵A和B可交换。其必要条件是A和B为同阶方阵

• 但矩阵的乘法满足结合律和分配律
  （1）(AB)C=A(BC)     （矩阵乘法的结合律）
  （2）k(AB)=(kA)B=A(kB)  （数和矩阵的结合律）
  （3）A(B+C) = AB+AC   （矩阵乘法的左分配律）
  （4）(B+C)A=BA+CA    （矩阵乘法的右分配律）

• 当k和t为正整数时，有A^kA^t=A^k+t, (A^k)^t=A^kt.

• 两个同阶上三角矩阵的积也是上三角形矩阵，两个同阶下三角形矩阵和两个同阶对角矩阵的乘积也是仍为下三角形矩阵和对角矩阵，乘积的对角元为两个矩阵对应对角元的乘积。
  

1.1.4 线性方程组的矩阵形式

含有m个一次方程n个未知数的方程组成为mxn型线性方程组，简称mxn型方程组。

将方程组表述为矩阵形式Ax=b，A称为方程组的系数矩阵，b称为方程组的常数向量。由A和b合起来所构成矩阵[A,b]叫做方程组的增广矩阵。

当b=0时，方程组称为其次线性方程组，b不等于0时，方程组称为非齐次线性方程组。

1.1.5 矩阵的转置

定义1-5：把mxn矩阵A的行与列的位置互换所得到的nxm矩阵叫做A的转置矩阵，记作A_T或A’

• 矩阵转置的性质：
  （1）(A^T)^T
  （2）(A+B)^T= A^T+B^T
  （3）(kA)^T=kA^T
  （4）(AB)^T=B^TA^T

1.1.6 对称矩阵和反称矩阵

定义1-6：设A=[a_ij]_mxn,若A^T=A，则称A为对称矩阵，若A^T= -A,则称A为反称矩阵。

• 对称矩阵的特点是关于主对角线对称的元素相等；
• 反称矩阵的特点是关于主对角线对称的元素互为相反数，对角元都为零。
• 设A，B都为彤姐对称矩阵（反称矩阵），则AB是对称矩阵等价于AB=BA。

1.2 向量与分块矩阵

定义1-7：n个有次序的数a1,a2,…,an所组成的数组成为n元向量，这n个数成为该向量的n个分量

• 分量都为零的向量成为零向量
• $$用e_i\in R^n表示第i个分量为1，其余分量都为0的n原列向量，即单位向量$$
• 若干个同元数的列向量的集合叫做列向量组；若干个同元数的行向量的集合叫做行向量组

1.2.2 分块矩阵

定义1-8：用若干条纵贯整个矩阵的横线和竖线把矩阵A分成许多小的子矩阵，以这些小块为元素的形式上的矩阵称为A的分块矩阵

• 对两个分块矩阵A和B进行加法运算，则需要A和B同型，且采用相同的分块方法
• 对两个分块矩阵A_mxl和B_lxn进行乘法运算，则对A的列和B的行采用相同的分块方法
• $$e_i^{T}A{e}_j表示A的（i，j）元a_{ij}$$

1.3 初等变换与初等矩阵

线性方程组的初等变换

由于线性方程组与它的增广矩阵一一对应，并且方程组中的每个方程对应增高广矩阵中的一行
类似地，对于矩阵的初等行变换：
定义1-9：设A是mxn矩阵，i不等于j，下面三种变换称为矩阵的初等行变换

类似地，将上述定义中的行换成列，即得到矩阵的初等列变换。

矩阵的初等变换都是可逆的
定义1-10：如果矩阵A经过有限次初等变换变成B，则称矩阵A与B等价，记作A->B（或A~B），也叫作A与B相抵。
当nxn方程组Ax=b有唯一解时，即能够将A等价化为E，则可以使用的解法：用初等行变换将增广矩阵[a,b]化为[E,c]，则其姐为x=c

1.3.2 初等矩阵

初等举着你的作用是通过其建立起初等变换与矩阵乘法之间的联系。
定义1-11：由单位矩阵E经过一次初等变换所得到的矩阵叫做初等矩阵，与三种初等变换相对应，有三种初等矩阵
（1）对调E的i和j两行（或列）所得到的仿真叫做对调矩阵，记作E_i,j
（2）将E的第i行（或列）乘非零数k所得到的的仿真叫做倍乘矩阵，记作E_i(k)
（3）将E的第j行乘数k加到第i行（或将E的第i列乘数k加到第j列），所得到的方阵叫做倍加矩阵，记作E_i,j(k)

• 初等矩阵的性质
  （1）性质1-1（转置操作时，倍加变换引起初等矩阵改变）
  
  （2）性质1-2
  
  （3）性质1-3
  

矩阵的等价标准型

定理1-1：对于任何仿真A，只用有限次倍加行变换（或有限次倍加列变化）都能够将A化为上三角形矩阵，即一定有倍加矩阵Pi（i=1,2,…,k）[或Qj(j=1,2,…,l)]，使得Pk···P2P1A或（AQ1Q2···Ql）为上三角形矩阵*

定理1-2：对于任何mxn非零矩阵A，比能用初等变换将它化为形如

的矩阵F，即存在m阶初等矩阵Pk，···，P2，P1或n阶初等矩阵Q1，Q2，···，Ql，使得$$P_k\cdot \cdot \cdot P_2{P}_{1}A{Q}_1{Q}_2\cdot \cdot \cdot Q_l=F$$

矩阵F叫做A的等价标准形（相抵标准形）

第2章 方阵的行列式

本章内容：行列式的定义、性质、计算

2.1 n阶行列式的定义

从方阵A=[a_ij]_mxn中去掉a_ij所在的第i行和第j列所余下的n-1阶方阵称为a_ij的余子阵，记作A（i,j）
定义2-1：设A=[a_ij]_mxn，把下式叫做方阵A的行列式，记作det(A)或|A|

我们把a_ij的余子阵A(i,j)的行列式det(A(i,j))叫做a_ij的余子式，把（-1）^i+jdet(A(i,j))叫做a_ij的代数余子式，记作A_ij即$$A_{ij}=(-1{)}^{i+j}det(A(i,j))$$
下式称为det(A)按照第1列的展开式，
$$det(A)=a_{11}{A}_{11}+a_{21}{A}_{21}+...+a_{n1}{A}_{n1}+$$

2.2 行列式的性质

• 性质2-1 ：|A^T|=|A|
• 性质2-2：行列式|A|可按照其任一列或任一行展开，第j列和第i行的展开式如下

• 推论2-1：若方阵A的某列（行）的元素全为0，则|A|=0

在代数余子式向量的表述基础上，可以写成

• 引理2-1： 若方阵A和B只有第j列不同，则A和B的第j列的代数余子式向量相同
• 性质2-3（行列式的线性性质）

• 推论2-2：|kA|= kⁿ|A|（n为方阵A的阶数）
• 性质2-4：若方阵A中有两列（行）相同，则|A|=0
• 推论2-3：若|A|中有两列（或两行）成比例，则|A|=0
• 推论2-4： 若|A|中有一列（行）是另外两列（行）的和，则|A|=0
• 性质2-5：若对方阵A进行一次倍加列（行）变换得到B，则|A|等于|B|，即倍加行变换不改变行列式的值。
• 性质2-6：若对方阵A进行一次对调列（行）变换得到方阵B，则|A|=-|B|
• 性质2-7：行列式的某一列的每个元素乘另一列对应元素的代数余子式之和等于零，即

2.3 行列式的计算

2.3.1 按行（列）展开

2.3.2 化为三角形行列式

因为上三角形矩阵的行列式等于其对角元的乘积，所以可以通过有限次初等变换将所给的行列式化为上三角形行列式来进行计算

2.3.3 先化简再展开

2.3.4 范德蒙德行列式

2.3.5 各行（列）元素之和相等的行列式

2.3.6 箭形行列式

2.3.7 递推发及三对角行列式

2.4 分块三角形行列式及矩阵乘积的行列式

定理2-1 ：设A和B分别为m阶和n阶方阵，C为mxn矩阵，则有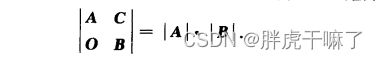

定理2-2：设A和B都是n阶方阵，则|AB|=|A|·|B|
推论2-5：设A为n阶方阵，k为正整数，则|A^k|=|A|^k

第3章 可逆矩阵及nxn型线性方程组

本章内容：矩阵可逆的条件、可逆矩阵的性质及求逆矩阵的方法，关于nxn型线性方程组有唯一解的冲要条件极其解法

3.1 可逆矩阵

3.1.1 可逆矩阵的定义

定义3-1：对于n阶方阵A，若存在n阶方阵B，使得AB=BA=E，则A叫做可逆矩阵（A矩阵可逆），B叫做A的逆矩阵，否则称A不可逆
定理3-1：若A是可逆矩阵，则A的逆矩阵是唯一的

3.1.2 伴随矩阵及矩阵可逆的条件

定义3-2：伴随矩阵

需要注意的是，伴随矩阵A中第i列的元素是A中第i行相应元素的代数余子式，转置后记录是为了方便将A和A直接相乘。

定理3-2：设A是n阶方阵，n>1，则AA=A*A=|A|E*
定理3-3：方阵A可逆的充要条件为|A|!=0，且当A可逆的时候，有：
$$|A^{-1}|=\frac{1}{|A|},A^{-1}=\frac{A^{\ast }}{|A|}$$

• 若A为n阶方阵，则有|A*|=|A|^n-1

定义3-3：对于方阵A，当|A|=0时，称A为奇异矩阵；当|A|！=0时，称A为非奇异矩阵
（非奇异矩阵即可逆矩阵，奇异矩阵即不可逆的矩阵。仅仅是定义方式不同，是否奇异取决于其行列式是否为0；是否可逆取决于是否能够找到矩阵B，使得AB=BA=E。
推论3-1：若方阵A和B满足AB=E，则A和B都可逆，且A^-1=B，B^-1=A

• 关于证明方阵可逆的方法，至此有两种：
  方法1：通过证明|A|！=0来证明A可逆
  方法2：找到方阵B，证明AB=E

• 可逆矩阵A具有如下性质
  （1）A^-1也可逆，且有（A^-1）^-1=A
  （2）A^T也可逆，且（A^T）^-1=(A^-1)^T
  （3）若数k！=0，则kA也可逆，且（kA）^-1=k^-1A^-1
  （4）当A和B 是同阶可逆方阵，则AB也可逆，同时(AB)^-1=B^-1A^-1
  在第四条性质基础上做拓展，有：
  若A1，A2,…,Ak为同阶可逆方阵，则A1A2····Ak也可逆，且
  （A1A2···Ak）^-1=Ak^-1···A2^-1A1^-1
  同理，将所有矩阵归为同一矩阵时，(A^k)^-1=(A^-1)^k

3.1.3 求逆矩阵的初等行变换法

定理3-4：方阵A可逆的充要条件为A能表示成有限个初等矩阵的乘积
可逆矩阵的等价标准型是单位矩阵
推论3-2：方阵A可逆的充要条件是A与E等价
（等价即经过有限次初等变换，A能够转换为B）
推论3-3：在矩阵A的左（右）端乘可逆矩阵，等价于，对A进行有限次初等行（列）变换
推论3-4：mxn矩阵A与B等价（相抵）的充要条件是存在m阶可逆矩阵P和n阶可逆矩阵Q，使得PAQ=B

关于求解逆矩阵的初等行变换法或列变换法的原理：

当A可逆时，有A^-1 可逆，A ^-1[A,E] = [E,A^-1]，即使用有限次初等行变换一定能够将[A,E]化为[E,A^-1]。选用行变换而非列变换的原因是为了使得行分块矩阵的两个矩阵块作相同的变换。
同理，可以对[A,E] ^T使用初等列变换的方式，得到矩阵[E,A^-1]^T

• 设A和B都是n阶可逆矩阵，则分块上三角形矩阵
  是可逆矩阵，其行列式为|A|·|B|，逆矩阵为
  

3.1.4 矩阵方程

3.2 nxn型线性方程组

3.2.1 nxn型齐次线性方程组

对于齐次线性方程组Ax=0一定有解x=0，将这个解成为Ax=0的零解，若u!=0也是Ax=0的解，则称u是Ax=0的非零解。
齐次线性方程组的解的情况：
（1）只有零解
（2）有非零解
定理3-5：nxn型其次线性方程组Ax=0只有零解（有非零解）的充要条件为|A|!=0（|A|=0）

3.2.2 nxn型非齐次线性方程组

对于非齐次线性方程组Ax=b，其解的情况有：有唯一解，有无穷多解，无解。我们只研究有唯一解的充要条件
定理3-6：nxn型非齐次线性方程组Ax=b有唯一解的充要条件是|A|！=0（即A可逆），其解为x=A^-1b

定理3-7（Cramer法则）：当|A|！=0时，nxn型非齐次线性方程组Ax=b有唯一解，
$$x_i=\frac{B_i}{A}（i=1,2,...,n）$$
其中，B_i是将A的第i列换为b所得的矩阵

第4章 空间的平面与直线

解析几何的内容分两章讲解。第九章研究空间的曲面与曲线，第四章以向量为工具研究空间的平面与直线。主要内容：介绍向量的基本概念 、线性运算数量积、向量积和混合积等向量代数知识，然后用他们来建立空间的平面和直线的方程，并讨论平面和直线相互间的位置（夹角和距离）关系。

4.1 向量与空间直角坐标系

定义4-1：一个即有大小又有方向的量叫做向量（矢量），用一个上面加箭头的字母表示
与始点无关的向量叫做自由向量。

4.1.2 向量的线性运算及投影

定义4-2：三角形法则或平行四边形法则

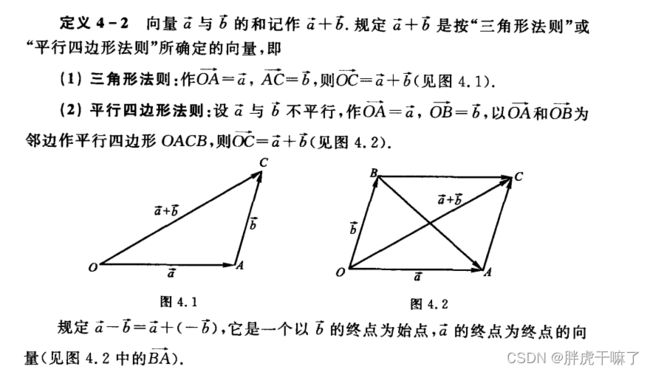
定义4-3：数lambda与向量a的乘积记作lambda·a，规定lambda·a是一个向量，它的长度为

关于其方向，在lambda>0时，与a方向相同；当lambda<0时，与a方向相反；当lambda=0时，lambda·a=零向量，其方向任意。

• 向量的加法和向量与数的乘法这两种运算统称为向量的线性运算。
• 

（1）加法交换
（2）加法结合
（3）0的加法
（4）相反和加法
（5）数乘结合、数乘交换
（6）1做数乘
（7）数乘，数对向量分配
（8）数乘，向量对数分配

4.1.3 空间直角坐标系

• 在空间选定一点0作为原点，过O点作三个两两垂直的数轴，分别称为x轴，y轴和z轴，统称为坐标轴，他们的正向按照x,y,z的次序符合右手法则。由原点和这三个坐标轴所组成的系统叫做空间直角坐标系，简称Oxyz坐标系。
• 在空间直角坐标系中，每两个坐标轴都决定一个平面，分别称为Oxy面，Oyz面，和Ozx面。
• 三个坐标面把整个空间氛围八个部分，每一个部分称为一个卦限。

4.1.4 向量的坐标与点的坐标

• 在Oxyz坐标系中，分别与x,y,z轴同向的单位向量叫做这个坐标系的基本向量，分别用i,j,k表示。
• 空间中全体向量的集合叫做三维几何空间。在Oxyz坐标系中，它可以用从原点出发的所有向量的集合来表示。

4.2 数量积、向量积和混合积

在向量的线性运算之外，在此节将介绍向量的另外三种运算。

4.2.1 数量积

定义4-4：两个向量a与b的数量积（点乘积）是一个数，记作a·b，规定有
$$a\cdot b=|a||b|cos\theta$$
而数量积的物理意义则为：物体在与水平线成theta角的力\vec F的作用下，若产生水平位移\vec s，则力\vec F对物理所做的功为：
$$W=F\cdot s$$

• 向量的数量积与向量的投影有着如下联系：
  

• 数量积的性质（lambda为数）
  $$\begin{gathered} a\cdot a\ge 0,a\cdot a=0⟺a=0（大于等于0） \\ a\cdot b=b\cdot a（反身性） \\ (\lambda a)\cdot b=a\cdot (\lambda b)=\lambda (a\cdot b)（数字在数量积中的位置任意） \\ (a+b)\cdot c=a\cdot c+a\cdot c（数量积的分配律） \end{gathered}$$

对于数量积，在几何向量和代数向量两种表示方法上，有：两个向量的数量积等于它们的坐标的乘积之和。

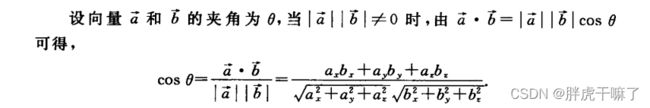
按照上式可以求出向量a与b之间的夹角theta，以及a在b上的投影(a)_b和投影向量
$$\frac{b}{|b|}\cdot (a{)}_b$$

4.2.2 向量积

定义4-5：两个向量a与b的向量积（也叫叉乘积）是一个向量，记作axb，规定：
（1）叉乘的长度为|axb|=|a||b|sin (theta)（其中theta为a和b的夹角）
（2）它的方向与a和b都垂直，且按a，b，axb的次序符合右手法则。

• 关于向量积的几何意义：当a与b不平行时，|axb|表示以a和b为邻边的平行四边形的面积

• 关于向量积，具有如下性质：
  （1）$$a\times a=0$$
  （2）$$a\times b=—b\times a$$
  （3）$$(\lambda a)\times b=a\times (\lambda b)=\lambda (a\times b)（数字在向量积中的位置任意）$$
  （4）
  $$(a+b)\times c=a\times c+b\times c（叉乘的分配律）$$

关于几何向量和代数向量在向量积上的关系：

4.2.3 混合积

定义4-6： 三个向量a,b,c的混合积是一个数，记作（a,b,c），规定（a,b,c）=(axb)·c
关于混合积的几何意义：
以三个非零向量a,b,c为棱作一个平行六面体，其底面积为|axb|，高为|c| |cos(theta)|，于是该平行六面体的体积为：

即，三个向量的混合积的绝对值表示以这三个向量为棱的平行六面体的体积。
且，若三个向量依次序符合右手法则，则V=（a,b,c）,否则V=—（a,b,c）

4.2.4 向量间的关系

定理4-1： 设a,b,c都是非零向量，theta为a与b的夹角，则

4.3 空间平面及其方程

主要介绍了空间直角坐标系中根据确定平面的条件建立相应的平面方程

4.3.1 平面的点法式方程

• 与平面垂直的非零向量叫做该平面的法向量。
• 显然，平面上的任何一个向量都与其法向量垂直。由于平面由其上一点和它的法向量唯一确定，以此我们建立平面的点法式方程。
  
  在知晓该平面上两个不共线的向量，以及该平面上的一点时，可以使用行列hi，得到该平面方程。
  

4.3.2 平面的一般式方程

将平面的点法式方程整理成Ax+By+Cz+D=0，其中D=-(Ax0+By0+Cz0)，将这个方程称为平面的一般式方程。

• 对于一些特殊的三元一次方程，其对应的平面的特点：
  （1）当D=0时，一般是方程表示一个过原点的平面。
  （2）当D！=0，且A,B,C中只有一个为0时，平面平行于某个坐标轴
  （3）当D！=0，且A,B,C中有两个为0时，平面平行于某个坐标面。

4.3.3 平面的截距式方程

当abc！=0（都不等于0）时，平面$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$$
平面x,y,z轴上的截距分别为a,b,c，这种形式的平面方程称为平面的截距式方程。

4.3.4 平面的三点式方程

考虑到空间中不共线的三点可以唯一地确定一个平面，所以

因为三个向量共面，故混合积为0，则有

4.3.5 同轴平面束

• 经过同一条直线的所有平面的集合叫做同轴平面束。

上式表示的平面经过π1和π2的交线：直线l，该方程是以直线l为轴的平面束方程。

4。4 空间直线及其方程

本节在空间直角坐标系中更具确定直线的条件，建立相应的直线方程

4.4.1 直线的点向式方程与参数式方程(和两点式方程)

直线的方向向量：与直线平行的非零向量叫做该直线的方向向量。其三个坐标称为该直线的方向数。

• 由一点和方向向量所确定的直线方程叫做该直线的点向式方程，也叫对称式方程。

值得一提的是，当三个方向数中存在零时，在形式上仍然可以用上式来表示直线，如：
$$\frac{x-x0}{2}=\frac{y-2}{0}=\frac{z-z0}{-3}$$

• 直线的参数式方程：
  $$点P（x,y,z）在直线l上⟺P0P平行于s⟺存在数t，使得P0P=ts$$
  

• 直线的两点式方程
  

4.4.2 直线的一般式方程

当给定两个相交的平面，所交直线就唯一确定；但给定一条直线时，可以随机选取任意两个经过该直线的平面进行联立，得到方程组，故而，直线的一般式方程不唯一

• 直线的一般式方程转为对称式方程较为简单：
  
• 对于直线的对称式方程转化为一般式方程，有如下三种方法：
  （1）代入法确定一个点，叉乘一般式中平面的两个法向量，可以得到方向向量，可以得到点向式方程（对称式）
  （2）代入法确定两个点，连线，得到方向向量，
  （3）令其中一个变量z=t，求出该之下你的参数式方程，再转为对称式方程
  
  

4,5 位置关系、夹角与距离

4.5.1 两平面间的位置关系

• 平面间的关系有：重合、平行、相交
  

4.5.2 直线与平面间的位置关系

• 直线与平面的关系：直线在平面上，直线和平面平行、直线与平面相交（但不垂直）、直线与平面垂直

对于直线l（点向式）和平面π的方程分别为：

直线的方向向量s=[m,n,np]^T，平面的法向量n=[A,B,C]^T
（1）
$$直线l在平面\pi 上⟺s\perp n(s\cdot n=0)且点(x0,y0,z0)满足平面\pi 的方程⟺mA+nB+pC=0且Ax0+By0+Cz0+D=0$$
（2）

4.5.3 两直线的位置关系

• 对于两条直线，有共面和不共面两种，当共面时，两直线有重合、平行和相交三种情况
  对于直线间关系的判断，借用了两条直线点向式方程中的方向向量和两直线上点的连线来探究。
  当两直线共面时，两方向向量和两直线上点的连线向量，共三向量，三向量共面，即三向量的混合积为0，即三向量的行列式为0，则直线共面；
  在共面的情况下，
  当两直线重合，有两方向向量，以及连线向量的三个坐标值成比例；
  当两直线平行，有两方向向量的坐标值成比例，但并不与连线向量成比例；
  当两直线相交，等价于两方向向量和连线向量共面且两方向向量间不平行（坐标值不成比例）。
  注，在相交时，条件并不能保证满足三向量的行列式为0，从而不能保证两直线确实位于同一平面上，所以在相交的判断条件上，需要同时满足混合积为0和两向量不平行两个条件

4.5.4 直线和平面相互间的夹角

• 可以通过向量的夹角来且直线与直线、平面与直线、平面和平面的夹角
  

对于直线间、平面间、直线和平面间的夹角，由于元素间并没有方向可研，故而其夹角应该取较小的一个，小于π/2

4.5.5 距离

以向量为工具，研究点到直线（两条平行直线）、点到平面（两个平行平面、直线与平行于该直线的平面之间的距离）以及两条异面直线间的距离。

• （1）点到直线的距离（向量积）
  （两个（不共线的）向量的叉乘的大小表示以两向量为临边的平行四边形的面积）
  
  
  可以看出，两条平行直线的距离即为其中一条直线上的一点到另一条直线的距离

• （2）点到平面的距离（数量积）
  

可以看出，与平面π平行的直线l到π的距离为l上的任一点到π 的距离；两个平行平面之间的距离为其中一个平面上的任一点到另一个平面的距离

• （3）两条异面直线的距离（混合积和向量积）
  
  

第5章 向量组的线性相关性和矩阵的秩

本章研究向量组的线性相关性、向量组的秩和极大无关组，以及矩阵的秩。
关于矩阵和向量组的关系：一方面要用向量组的线性相关性和其秩的基本知识研究矩阵的秩；另一方面，将向量组写成矩阵的形式，通过矩阵来研究向量组的问题。

5.1 向量组的线性相关性和矩阵的秩

将线性方程组Ax=b，写成向量形式，有a1x1+a2x2+…+anxn=0。由方程组的向量形式可知，方程组Ax=b有解的充要条件是存在n个数k1,k2,…,kn，使得 k1a1+k2a2+…+knan=b
定义5-1：对于向量组a1,a2,a3,…,an,b，若存在n个数k1,k2,…,kn，使得b=k1a1+k2a2+…+knan，则称向量b是向量a1,a2,…,an的线性组合，或称向量b能由向量a1,a2,…,an的线性表示
定理5-1：设Ax=b是mxn型线性方程组
（1）方程组Ax=b有解等价于向量b能由A的列向量组线性表示
（2）方程组Ax=b有唯一解等价于向量b能由A的列向量组a1,a2,…,an线性表示且表达式唯一

5.1.1 向量组的线性相关性

对于mxn型齐次线性方程组Ax=0有非零解
等价于a1x1+a2x2+…+anxn=0有非零解
等价于，存在n个不全为零的数k1,k2,…,kn，使得k1a1+k2a2+…+knan=0
定义5-2（向量组的线性相关性）：对于向量组a1,a2,…,an，
（1）若存在n个不全为零的数k1,k2,…,kn，使得
k1a1+k2a2+…+knan=0
则称该向量组线性相关
（2）若仅当k1,k2,…,kn（x1,x2,…,xn）全为0时，才使得
x1a1+x2a2+…+xnan=0成立，则称该向量组线性无关
定理5-2：设A=[a1,a2,…,an]
（1）向量组a1,a2,…,an线性相关（无关）等价于齐次线性方程组Ax=0有非零解（只有零解）
（2）当A为方阵时，向量组a1,a2,…,an线性相关（无关）等价于|A|=0（|A|!=0）
（3）可逆矩阵的列向量组一定线性无关

• 含有零向量的列向量组一定线性相关
  定理5-3：向量组a1,a2,…,an(n>=2)线性相关的冲要条件是该向量组中至少有一个向量可以由其他n-1个向量线性表示
  定理5-4：若向量组a1,a2,…,an线性无关，而向量组a1,a2,…,an,b线性相关，则向量b可由a1,a2,…,an线性表示且表达式唯一
  定理5-5：向量组I为a1,a2,…,ar，向量组II为a1,a2,…,ar,ar+1,…,an
  （1）若向量组I线性相关，则向量组II也线性相关
  （2）若向量组II线性无关，则向量组I也线性无关
  定理5-6：设r元向量组I委a1,a2,…,am，s元向量组II为b1,b2,…bm，r+s元向量组III为c1,c2,…,cm

（1）若向量组I和II中有一个线性无关，则向量组III也线性无关
（2）若向量组III线性相关，则向量组I和II都线性相关

5.1.2 向量组的秩和极大无关组

定义5-3：在向量组V中，若有含r个向量的子向量组线性无关，并且V中任何含r+1个向量的子向量组（当V中向量多于r个时）都线性相关，则把r叫做向量组V的秩
若向量组V的秩为r，则V中含r个向量的线性无关的子向量组叫做V的极大线性无关组（极大无关组，最大无关组），即向量组V的秩反映的是向量组V中所含线性无关向量的最大个数
向量组V线性无关（相关），等价于，向量组V的秩等于（小于）其所含向量的个数
note：对于只含零向量的向量组，规定其秩为0，没有极大无关组。
note：对于非零的向量组，其秩存在且唯一，存在极大线性无关组，但一般不唯一
定理5-7：向量组V中的每个向量都可以由其极大无关组唯一地线性表示

5.2 矩阵的秩

矩阵的秩是矩阵的一个重要的数值特性，可以用来求向量组的秩，从而判断向量组的线性相关性，又在方程组问题的研究中起着重要作用

5.2.1 矩阵的秩的概念

定义5-4：矩阵A的行向量组的秩和列向量组的秩分别叫做矩阵A的行秩和列秩
定义5-5：设A为mxn矩阵，1<=k<=min{m,n}，由矩阵A的任意k个行和k哥列相交处的k^2个元素按照原来的相对位置所构成的方阵叫做矩阵A的k阶子阵，其行列式叫做矩阵A的k阶子式

• 当一个向量组所构成的矩阵A为方阵时，该向量组线性无关对应于矩阵A的行列式是不等于零。考虑到我们前面将极大无关组所含向量的个数定义为向量组的秩，可以有如下想法：将一个矩阵（未必是方阵）的最高阶非零子式的阶数定义为该矩阵的秩
  定义5-6：矩阵A中非奇异子阵的最高阶数（即非零子式的最高阶数）称为矩阵A的秩，记作r(A)，
  当A为零矩阵时，规定r(A)=0
  设A为mxn矩阵，由矩阵的秩的定义可知：
  （1）r(A)<=m且r(A)<=n
  （2）

（3）A的增广矩阵的秩不小于A的秩，即r([A,B])>=r(A)
（4）当k！=0时，r（kA）=r（A）

5.2.2 矩阵秩的性质

性质5-1：

性质5-2（三秩相等定理）：

定理5-8：设A为mxn矩阵，P为m阶可逆矩阵，若有B=PA，则A中任意r个列向量

和相应的列向量

满足相同的线性表达式，从而具有相同的线性相关性
推论5-1：
在定理5-8的基础上，有

性质5-3：设A为mxn矩阵，P和Q分别是m阶和n阶可逆矩阵，则r(PA)=r(AQ)=r(PAQ)=r(A)
推论5-2：初等变换不改变矩阵的秩

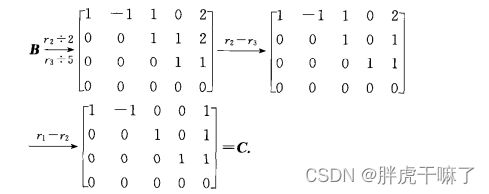
在求矩阵的秩的问题上，我们可以采用对A做初等行变换的方法， 将其转换为行阶梯矩阵B，

将B中每个非零行的第一个非零元素所在的那些行和列相交处的元素构成的子阵是一个非奇异子阵，

这个非奇异子阵的阶数是矩阵B和A的阶数

• 对于行阶梯矩阵B的特点有：
  （1）它的非零行向量都位于矩阵的前几行
  （2）每个非零行向量的第一个非零元素的列标随着行标的增大而严格增大
  于是，使用初等行变换求矩阵的秩的方法为：用初等行变换把矩阵化为行阶梯矩阵，这个行阶梯矩阵的非零行向量的个数就是该矩阵的秩

继续对矩阵B做初等行变换，可以得到矩阵A的行最简形C，矩阵C的特点：它是非零行的第一个元素都为1，且这些1所在列的其他元素都为零的行阶梯矩阵。

至于对矩阵C，继续做初等列变换可以化为标准型

性质5-4：

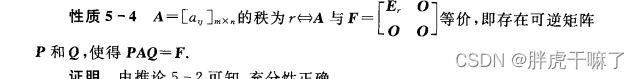
A的等价标准形F由A的秩唯一确定，故A的等价标准形是唯一的

性质5-5：设A,B,C分别为mxn，sxt，mxt矩阵，则

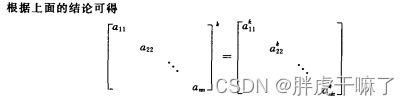
性质5-6：设A为mxk矩阵，B为kxn矩阵，则有

性质5-7：设A,B分别为mxn和mxk矩阵，则r([A,B]) <= r(A) + r(B)
性质5-8：设A和B都是mxn矩阵，则r(A+B)<=r(A)+r(B)
综合性质5-7和5-8，有r(A+B)<= r([A,B])<= r(A)+r(B)

5.2.3 满秩矩阵

定义5-7：设A为n阶方阵，当r(a)=n时，A叫做满秩矩阵；当r(A)
对于满秩矩阵：
定理5-9：设A为n阶方阵，x和b为n元列向量，则下列命题互为充要条件
（1）A为满秩矩阵
（2）A为非奇异矩阵
（3）A为可逆矩阵
（4）Ax=0只有零解
（5）Ax=b有唯一解
（6）A的行向量组和列向量组都是线性无关的

5.3 矩阵的秩在向量组中的应用

5.3.1 判断向量组的线性相关性

以所给向量组为列构造矩阵A，根据三秩相等定理，可以通过求A的秩来得知向量组的秩，从而可以判断向量组的线性相关性。

5.3.2 求向量组的极大无关组

用初等行变换将矩阵A化为行阶梯矩阵B，通过B的类向量组的极大无关组来找到A的列向量组的极大无关组，通过B中的列向量所满足的表达式来求出A的列向量所满足的表达式

5.3.3 等价向量组

定义5-8：若向量组I：b1,b2,…,bn中的每个向量都能由向量组II:a1,a2,…,an线性表示，则称向量组I能由向量组II线性表示

• 若向量组I和II能够互相线性表示，则称两个向量组等价（不丢失信息）

A能够通过B线性表示，则A可以通过变换（不要求初等）转化成矩阵B；
需要注意的是，向量组等价是一个向量组中的所有向量能够通过另一组中的向量们线性表示；而矩阵等价的含义，是将矩阵A通过初等变换转化为矩阵B。
个人理解下，向量组等价表示不丢失或不增添更多的信息，故而一个向量组和它的极大无关组是等价的，一个向量组的两个极大无关组之间也是等价的。

需要注意的是，由于矩阵形式的线性表示B=AP中，P在A右侧，故而在方程组中，P是经过矩阵转置后，才填写对应位置的系数处的
定理5-10：向量组b1,b2,…,bn能够 由向量组a1,a2,…,am线性表示，等价于存在矩阵P（不要求可逆或线性无关，即不限制矩阵A的信息丢失），使B=AP，其中A=[a1,a2,…,am],B=[b1,b2,…,bn]
定理5-11：若向量组I能由向量最II线性表示，则r(I)<=r(II)
推论5-3：若向量组I和II等价，则r(I)=r(II)

定理5-12（极大无关组的等价定义）：若向量组V中有r个向量a1,a2,…,ar线性无关，并且V中的任一向量都可以由a1,a2,…,ar线性表示，则a1,a2,…,ar是向量组V的一个极大（线性）无关组
（另一种定义：若向量组V的秩为r，则V中含r个向量的线性无关的子向量组叫做V的极大线性无关组）
定理5-13：向量组I：b1,b2,…,bn能由向量组II：a1,a2,…,am线性表示的充要条件为r(a1,a2,…,am,b1,b2,…,bn)=r(a1,a2,…,am)
推论5-4：向量组a1,a2,…,am与向量组b1,b2,…,bn等价的充要条件为r(a1,a2,…,am,b1,b2,…,bn)=r(a1,a2,…,am)=r(b1,b2,…,bn)

第6章 线性方程组

在本章中，研究线性方程组有解的充要条件，解的结构，以及线性方程组的解法。

6.1 线性方程组解的存在性

6.1.1 齐次线性方程组有非零解的充要条件

** 定理6-1：mxn型齐次线性方程组Ax=0有非零解（只有零解） ，等价于，r(A)

6.1.2 非齐次线性方程组解的存在性

** 定理6-2：设Ax=b是mxn型非齐次线性方程组，则**
（1）Ax=b有解，等价于，r([A,b])=r(A)
（2）Ax=b有唯一解，等价于，r([A,b])=r(A)=n

• 即，当r([A,b]) ！=r(A)时，Ax=b无解；
• 当r([A,b])=r(A)=n时，Ax=b有唯一解；
• 当r([A,b])=r(A)

6.1.3 几何应用

使用线性方程组和矩阵的秩研究空间解析几何中的平面与直线问题。

平面间的关系转化为Ax=b方程的解的存在性的问题，求平面交点或交线的运算自然转化为解方程组的计算：
（1）三个平面交于一点，iff，方程组Ax=b有唯一解，iff，r([A,b])=r(A)=3
（2）三个平面相互重合，iff，方程组Ax=b有无穷多解并且只有一个独立的方程，iff，r([A,b])=r(A)=1
（3）三个平面交于一条直线，iff，方程组Ax=b有无穷多解并且有两个独立的方程，iff，r([A,b])=r(A)=2

关于直线和平面之间的相互关系：

（1）直线l与平面π相交，iff，方程组Au=b有唯一解，iff，r([A,b])=r(A)=3；
（2）直线l在平面π上，iff，方程组Au=b有无穷多解且l的两个方程独立，iff，r([A,b])=r(A)=2且A的前两个行向量线性无关；
（3）直线l与平面π平行，iff，方程组Au=b无解且l的两个方程独立，iff，r([A,b])=3，r(A)=2且A的前两个行向量线性无关。

6.2 线性方程组解的性质、结构和解法

将在本节讲述线性方程组解的性质、结构和用矩阵的初等行变换求解线性方程组的方法

6.2.1 线性方程组的解的性质

设b！=0，方程组的解具有如下性质：

（1）（齐次线性方程组的解的线性组合仍为齐次线性方程组的解）
（2）（非齐次线性方程组的解加上相同系数矩阵的齐次线性方程组的解，仍未非齐次线性方程组的解）
（3）（非齐次线性方程组的两个解之差为相同系数矩阵的齐次线性方程组的解）
（4）（齐次线性和非齐次线性的解的条件线性组合）

6.2.2 齐次线性方程组解的结构

• 一个方程组的所有解的一般表达式叫做这个方程的通解，研究方程组的解的结构即是研究其通解的表达形式
  定义6-1：齐次线性方程组Ax=0的解集S（全部解向量的集合）的极大无关组叫做该齐次线性方程组的基础解系

定理6-3：齐次线性方程组Ax=0的解集S的秩r(S)=n-r(A)，即Ax=0的基础解析所含的向量的个数为n-r(A)，其中n为未知数的个数，即A的列数

向量组v1,v2,…,vs为mxn型齐次线性方程组Ax=0的基础解系的充要条件是，v1,v2,…,vs是Ax=0的解，且它们线性无关，且s=n-r

6.2.3 非齐次线性方程组解的结构

当Ax=b有唯一解时，可知，解的结构无需讨论
下面对无穷多解的情况进行讨论
定理6-4：设u为非齐次线性方程组Ax=b的一个已知解（特解），v1,v2,…,vn-r为Ax=0的基础解析，则Ax=b的通解为x=k1v1+k2v2+…+k_n-r+u其中，k1,k2,…,kn-r为任意常数

6.2.4 利用矩阵的初等航变换解线性方程

由于对非齐次线性方程组的增广矩阵进行初等行变换并不改变方程的解，故而，可以使用初等行变换将非齐次线性方程组的增广矩阵转化为行最简性，然后求出这个行最简形所对应的方程组的通解，即可得到原方程组的通解，对于其次线性方程组，只需要初等行变换将其系数矩阵（而非增广矩阵了）转化为行最简形

第7章 向量空间及向量的正交性

向量空间是几何空间的推广，与线性方程组的解的理论有着密切的联系。本章中介绍向量空间的一些基本知识，包括向量空间的概念、向量空间的基与维数、向量在基下的坐标、过渡矩阵与坐标变换、向量的内机、正交基与施密特正交化方法、正交矩阵

7.1 向量空间

7.1.1 向量空间的概念

定义7-1：设V是n元向量的集合，如果V非空，并且对于向量的线性运算封闭（即对任意的v1 ∈ V，v2∈V，k∈R，都有vi+v2 ∈V，kv1∈V），则称V是一个向量空间。

• 只含有零向量的集合{0}是一个向量空间
• 所有n元是向量的集合Rⁿ是一个向量空间
• 齐次线性方程组Ax=0的所有解向量构成的集合S是一个向量空间，把它叫做这个齐次线性方程组的解空间
• 若V是一个 向量空间，则V一定含有零向量
  

定义7-2：设V1,V2是两个向量空间
（1）若V1包含于V2，则称V1是V2的子空间
（2）若V1包含于V2，且V2包含于V1，则称这两个向量空间相等，记作V1=V2

7.1.2 向量空间的基与维数

定义7-3：向量空间V的一个极大无关组叫做V的一个基，V的秩叫做V的维数，记作dim（V），若dim(V)=r，则称V为r维向量空间

定理7-1：设V是n维向量空间，m

7.1.3 向量在基下的坐标

定义7-4：设a1,a2,…,an是n维向量空间V的一个基，对任意向量b∈V，把满足b=x1a1+x2a2+…+xnan的有序数x1,x2,…,xn叫做向量b在这个基下的坐标。x=[x1,x2,…,xn]^T叫做向量b在这个基下的坐标向量
对于矩阵A=[a1,a2,…,an]，则上式可以表示为矩阵形式Ax=b，则，求向量b在基A下的坐标，就是求解一个线性方程组。

7.1.4 过渡矩阵与坐标变换

对于同一个向量，在不同基下的坐标向量一般是不同的，下面探究这两个坐标向量之间的联系。
设a1,a2,…,an为n维向量空间V的一个基（旧的基），则V的另一个基（新的基）b1,b2,b3,…,bn能够由旧的基线性表示，设：

旧的基转换为新的基，做列变换是应该的，故而为了保证矩阵在形式上的意义，应该使得B=AP。而在对矩阵展开成方程组的过程中，注意，P的元素显然需要转置之后进行对应位置的抄写，以满足A的行与P的列相乘

• 注意，由于mxn和nxn矩阵相乘的结果矩阵，其列向量组是线性无关的，故而可知P是可逆的。

定理7-2：设n维向量空间V中的向量b在旧基a1,a2,…,an到新基b1,b2,…,bn下的坐标向量分别为x（旧）和y（新），从旧基到新基的过渡矩阵为P，则有坐标变换公式x=Py，即y=P^-1x
简证：v=Ax=By=APy，得知A（x-Py）=0，由定理6-1：mxn型齐次线性方程组Ax=0只有零解，iff，r(A)=n（即列向量组线性无关），可化简：x-Py=0，得证

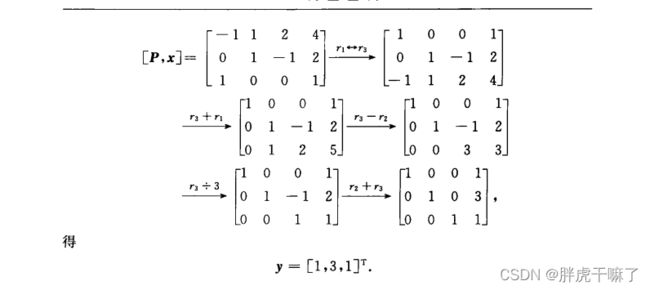
由上题，第一问应用到的一个技巧：对旧、新两个基组成的矩阵的增广矩阵[A,B]=[A,AP]，可以进行行变换得到[E,P]。关于可以进行以上转换的原因：行变换并不改变分块列向量之间的线性相关关系。且A在三维空间中为方阵，由三秩相等定理，知该方阵A为可逆矩阵。故而可以将增广矩阵转换为[E,P]
第二问，类似地，P^-1[P, x] = [E,y]

7.2 向量的正交性

本节中将空间解析几何中向量的数量积概念推广到实向量空间Rⁿ（在这里叫做“内积”），给出了向量的内积的定义，并进一步讨论向量的长度、夹角及正交性

7.2.1 向量的内积

将空间解析几何中，向量a和b的数量积定义为

定义7-5：（实向量内积）

内积公理（内积的性质）：

（1）（内积内翻转）
（2）（内积的数乘）
（3）（内积的加法）
（4）（自身做内积）
定义7-6：定义了内积的向量空间称为欧式空间
在定义了内积后，我们才能讨论向量的长度（内积的反身性）和角度（cos）

定义7-7：实向量的长度

• 向量的长度的性质：
  
  定义7-8：a！=0，b！=0时

7.2.2 正交向量组与施密特正交化方法

定义7-9：由两两正交的非零向量组成的向量组称为正交向量组，由单位向量组成的正交向量组称为标准正交向量组
定理7-3：正交向量组一定线性无关

为了从一个线性无关的向量组求出一个与之等价的正交向量组，可以使用以下方法：

关于上述方法的个人理解，对于非第一个维度的aj，他们的转化方法，是在aj向量的基础上不断减去其他转换过的向量bi的分量，这个分量的计算，是aj在bi单位向量上的投影的大小，再乘上bi的方向（公式化为bi的单位向量，长度为1，方向与bi同）

• 欧式空间的基，常常使用正交向量组或标准正交向量组
  定义7-10：当欧式空间V的一个基为正交向量组时，则称这个基为V的正交基；当V的基为标准正交向量组时，则称这个基为标准正交基

7.2.3 正交矩阵

定义7-11：若实方阵A满足A^TA=E,则称A为正交矩阵

• 当A为方阵时，下述三个条件是等价的，都是正交矩阵的定义
  （1）A^TA=E
  （2）A^-1=A^T
  （3）AA^T=E

• 正交矩阵是一种特殊的可逆矩阵（方阵）

• 正交矩阵的性质：
  设A,B为同阶正交矩阵
  （1）A可逆，且A^-1=A^T
  （2）A^T为正交矩阵（A^-1为正交矩阵）
  （3）AB为正交矩阵
  （4）|A|=±1

定理7-4：实方阵A为正交矩阵的充要条件是A的列向量组为标准正交向量组

以下为正价矩阵的等价的证明

• 注意：关于以上的充要条件的证明中，列向量的乘法的两个式子，一个代表列向量标准，一个代表列向量间正交
• 对于正交矩阵的证明，有两种方法：
  （1）定义7-11：
  

（2）定理7-4：实方阵A的列向量组为标准正交向量组，iff，实方阵为正交矩阵

第8章 仿真的特征值与相似对角化

• 矩阵的对角化、化简曲面方程、求解微分方程组与解的稳定性分析等问题，都需要求解方阵的特征值和特征向量。
• 在本章中，介绍了方阵的特征值与特征向量的概念、性质，介绍了相似矩阵的概念，讨论了一个仿真的相似对角化，介绍实对称矩阵的相似对角化。

8.1 方阵的特征值及其特征向量

8.1.1 特征值与特征向量的概念及计算

定义8-1：设A为n阶方阵，λ为变量，把|λE-A|=0的根称为A的特征值（单根称作单特征值，重根称作重特征值）

8.1.2 特征值与特征向量的性质

8.2 相似矩阵