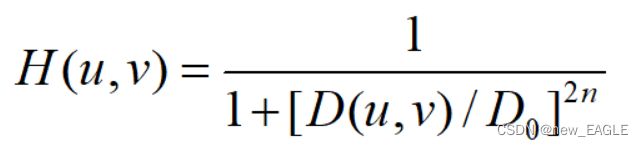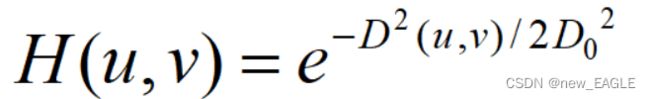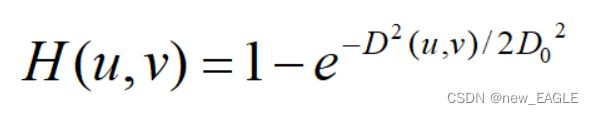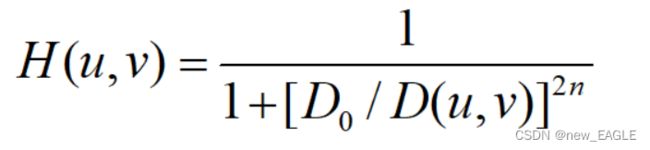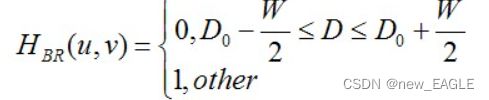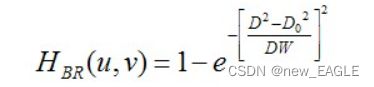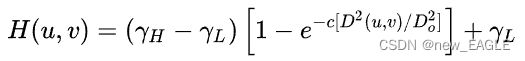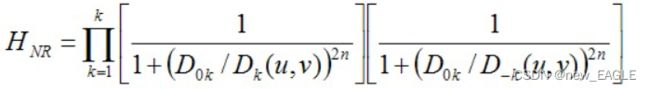Matlab之图像增强的频域增强

从上节的回顾中，我们知道了图像增强可以分为点增强、空间域增强，频域增强；

 

空间域增强是直接在图片上增强，有各种现成的算子可供使用；但对于频域增强来讲，他是需要将图片先转换为频域才能进行转换，频域一般是进行滤波，如低通滤波，高通滤波等，今天就来讲一下频域增强所用的滤波方式；

第一大部分：低通滤波器（保留低频，过滤高频）

第一，理想低通滤波器，低通滤波器的作用就是保存低频，过滤高频；内容就是设置一个定值来作为范围，超过这个数的部分为0，低于这个数的部位为1，举例：

%低通滤波器
clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);

m = 2*size(I, 1);%不乘2的话，D的范围减半以至于后面的部分都要减半，使得L无法成型
n = 2*size(I, 2);
x = -m/2 : (m/2-1);%获得在x方向的所有长度
y = -n/2 : (n/2-1);%获得在y方向上所有的长度
[X, Y] = meshgrid(x, y);%建立网格，方便进行计算到零点的距离，若步建立网格，会导致数组大小不兼容，建网格实际上是让他们的模板大小一样
D = sqrt(X.^2 + Y.^2);  %构造D矩阵，D是各位置与原点的距离
D0 = 80;  %D0为截止频率(中心频率)
H = double(D <= D0);%小于等于D0的位置为1，不满足的为0
J = fftshift(fft2(I, size(H, 1), size(H, 2))); %转换为频域再用fftshift进行平移，转换为与H相等大小的图像数据
K = J.*H;   %频域内滤波
L = ifft2(ifftshift(K));   %逆变换回到空域
L = L(1: size(I, 1), 1: size(I, 2));%因为L一开始是694*1040大小的，然后需要将其中转换为与原图片一样大的，若前面的M与N里面不乘以2的话，L的范围会比I小，同时显示出来的范围是不完整的

figure
subplot(121), imshow(I);
subplot(122), imshow(L);

因为我也是刚学，所以该程序是我从Matlab之图像增强技术（九）_我要糖的博客-CSDN博客_matlab图像增强

里面借鉴的，并且做了一些自己的理解；低频滤波器过滤掉高频使得图片边缘变模糊；

还有一种写法：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);
[m,n]=size(I);
M=floor(m/2);
N=floor(n/2);
H=zeros(m,n);
D0=60;
for i=1:1:m
    for j=1:1:n
        if(sqrt((i-m/2)^2+(j-n/2)^2)<=D0)
        H(i,j)=1;
        end
    end
end
J=fftshift(fft2(I));
K = J.*H;   
L = ifft2(ifftshift(K));
figure
subplot(121), imshow(I);
subplot(122), imshow(L);

相比较而言第二种方法更好理解一些，推荐第二种写法；

第二，巴特沃斯低频滤波器；

举例：

I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);

m = 2*size(I, 1);
n = 2*size(I, 2);
x = -m/2 : (m/2-1);
y = -n/2 : (n/2-1);
[X, Y] = meshgrid(x, y);
D = sqrt(X.^2 + Y.^2);%距离
D0 = 50;  %D0为截止频率
n = 6;      %阶数为6
H = 1./(1+(D./D0).^(2*n));%巴特沃斯的公式
J = fftshift(fft2(I, size(H, 1), size(H, 2))); %转换为频域再用fftshift进行平移
K = J.*H;   %频域内滤波
L = ifft2(ifftshift(K));   %逆变换回到空域
L = L(1: size(I, 1), 1: size(I, 2));

figure
subplot(121), imshow(I);
subplot(122), imshow(L);

上面这是巴特沃斯低通滤波器的公式； 

同样有第二种写法：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);
[m,n]=size(I);
M=floor(m/2);
N=floor(n/2);
H=zeros(m,n);
D0=60;
for i=1:1:m
    for j=1:1:n
        D=sqrt((i-m/2)^2+(j-n/2)^2);
        H(i,j)=1./(1+(D./D0).^(2*n));
    end
end
J=fftshift(fft2(I));
K = J.*H;   
L = ifft2(ifftshift(K));   
figure
subplot(121), imshow(I);
subplot(122), imshow(L);

推荐第二种写法；

第三，高斯低通滤波器

上面这个是高斯低通滤波器的函数，D为距离；举例 ：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);
[m,n]=size(I);
M=floor(m/2);
N=floor(n/2);
H=zeros(m,n);
D0=60;
for i=1:1:m
    for j=1:1:n
        D=sqrt((i-m/2)^2+(j-n/2)^2);
        H(i,j)=exp(-(D)/(2*(D0^2)));
    end
end
J=fftshift(fft2(I));
K = J.*H; 
L = ifft2(ifftshift(K)); 
figure
subplot(121), imshow(I);
subplot(122), imshow(L);

真的掌握了原理（还有一些细小的顺序也要记住），这些代码真的是很容易就有思路； 

第二大部分：高频滤波器（过滤低频，保留高频）

第一，高斯高通滤波器

上式为高斯高通滤波器的公式；举例：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);
[m,n]=size(I);
M=floor(m/2);
N=floor(n/2);
H=zeros(m,n);
D0=10;
for i=1:1:m
    for j=1:1:n
        D=sqrt((i-m/2)^2+(j-n/2)^2);
        H(i,j)=1-exp(-(D)/(2*(D0^2)));
    end
end
J=fftshift(fft2(I));
K = J.*H;  
L = ifft2(ifftshift(K)); 
figure
subplot(121), imshow(I);
subplot(122), imshow(L);

和高斯低通一样，就是改了一下公式；

第二，巴特沃斯高通滤波器

上式为巴特沃斯高通滤波器，举例：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = im2double(I);
[m,n]=size(I);
M=floor(m/2);
N=floor(n/2);
H=zeros(m,n);
D0=10;
for i=1:1:m
    for j=1:1:n
        D=sqrt((i-m/2)^2+(j-n/2)^2);
        H(i,j)=1./(1+(D0./D).^(2*n));
    end
end
J=fftshift(fft2(I));
K = J.*H;   
L = ifft2(ifftshift(K));  
figure
subplot(121), imshow(I);
subplot(122), imshow(L);

第三大部分， 带阻滤波器

因为我也是刚开始接触，所以我看了网上的很多的代码，我发现带租滤波器也分为很多种，如巴特沃斯带阻滤波器，理想带阻滤波器，高斯带阻滤波器；理想的带阻滤波器就是设置了一个环形范围，只要在这个范围之内的为0，在这个范围之外的的为1；

举例：学习的是Matlab之图像增强技术（九）_我要糖的博客-CSDN博客_matlab图像增强的代码：

clc
clear all
I = imread('dream.jpg');
I = rgb2gray(I);
I = imnoise(I, 'gaussian');
I = im2double(I);

m = 2*size(I, 1);
n = 2*size(I, 2);
x = -m/2 : (m/2-1);
y = -n/2 : (n/2-1);
[X, Y] = meshgrid(x, y);
D = sqrt(X.^2 + Y.^2);
D0 = 40;  
W = 20;   
H = double(or(D<(D0-W/2), D>(D0+W/2)));  %阻带为30到50，在这个范围内的为0，在这个范围之外的为1；  
orign = fftshift(fft2(I, size(H, 1), size(H, 2)));
K = orign.*H; 
picture = ifftshift(K);
picture=ifft2(picture);
picture = picture(1: size(I, 1), 1: size(I, 2));

figure
subplot(121), imshow(I);
subplot(122), imshow(picture);

也可以用for循环的形式；

第二，巴特沃斯带阻滤波器，大致内容与高频低频一样，就是在算的时候不一样，他这里需要得到每个点与噪声起始点的距离，也就是需要两个距离，同时公式也不一样

%D为距离，D0为中心频率，W为带宽，n为阶数；

第三，高斯带阻滤波器，公式为：

这三个带阻滤波器的代码，参考低频与高频，只需把公式改过来就可以使用；但是对带宽的选取需要自己斟酌；

第四大部分：同态滤波

同态滤波，一张图片的反射分量和照射分量是乘性的，如果直接傅里叶变化的话，对于傅里叶形式就是卷积，我们不要这种形式，为了避免这样，提前对他们进行log，这样傅里叶变换后就不是卷积形式了；同态滤波的作用是将光亮调整，让我们能看到暗中没法看到的，增加对比度，减小光照的影响；

 当rH （高频权重）大于1, rL（低频权重） 小于1可以达到滤低增高的目的，常数c控制高斯函数的陡峭度。D0越大，对细节的增强越好，归一化后的图像就越亮。每张图片的D0是不一样的，根据图片来定义； 

第五大部分：带通滤波器

带通滤波器的作用和带阻滤波器的功能相反，功能是让在一定范围内的信号可以通过，在其中的信号为1，在其之外的信号为0；公式是：1-带阻滤波器； 

第六大部分：陷波滤波器

像带阻滤波器也是可以滤波，但是他也会对噪声以外的信号进行衰减；像陷波滤波器是某个点进行衰减，其余部分不会被影响； 

上式为陷波滤波器的公式，因为傅里叶的周期性，所以一个噪声是对应一个对称点，Dk与D-k是分别对应两个距离;(关于中心点对称)；