RL 实践（2）—— 杰克租车问题【策略迭代 & 价值迭代】

• 参考：《Reinforcement Learning An Introduction》—— Richard S.Sutton
• 完整代码下载：[Handcraft Env] Jack’s Car Rental (Policy Iteration & Value Iteration)

---

1. 算法介绍

• 策略迭代policy iteration 和 价值迭代value iteration 都是用于解状态转移矩阵和奖励函数已知的 model-based RL 问题的方法，二者的详细说明请参考 强化学习笔记（4）—— 有模型（model-based）prediction 和 control问题（DP方法）
• 关于这两个方法的收敛性证明请参考 强化学习拾遗 —— 表格型方法和函数近似方法中 Bellman 迭代的收敛性分析

1.1 policy iteration 算法

• 算法流程：反复迭代执行以下两步，直到V收敛为止（常使用DP方法实现这个迭代）

  1. policy evaluation：迭代计算Bellman公式至收敛
     

  2. policy improve：根据$\pi$计算$q$，再对每个s贪心地找到使$q^{{\pi }_i}(s,a)$最大的a来更新 $\pi (s)$
     

1.2 value iteration 算法

• 算法流程：

  1. 使用 MDP 的 Bellman optimal 公式反复迭代计算至收敛，求出 $V^{\ast }$（常使用DP方法实现这步的迭代）
     

  2. 利用 $V^{\ast }$ 重构 $q^{\ast }$，从而对每个s贪心地找出动作 a，得 ${\pi }^{\ast }$
     

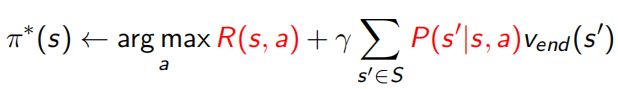
2. 杰克租车问题

• 这里使用强化学习圣经《Reinforcement Learning An Introduction》上的 Example 4.2 作为本次实践的环境，这是一个经典 model-based RL 问题，原书中描述如下
  
  简单概括一下吧

  1. Jack 承包了某租车公司的两个门店，每天会有一些人来租车和还车（还的车不一定都是对应门店出租的，也可能是公司其他门店出租的车还到他这里），每出租一辆车可以挣 10 元
  2. 车辆归还后，第二天才能再次出租
  3. 门店1每天的租车请求和还车数量都服从参数为 $\lambda =3$ 的泊松分布；门店2每天的租车请求和还车数量分别都服从参数为 $\lambda =4$ 和 $\lambda =2$ 的泊松分布
  4. 每个门店最多停放 20 辆车，停满之后客户会把车还到其他门店，我们不需考虑
  5. 为了最大限度满足两个门店的需求，每天晚上 Jack 可以在他的两个门店间转移一些车辆，转移一辆车成本 2 元，一晚上最多转移 5 辆车

  现在把它建模成一个 MDP 问题

  1. 状态集：每天晚上关门时两个门店的车辆数二元组 $s=\{(x,y)\},x,y\in [1,20]$
  2. 动作集：每天晚上 Jack 在两个门店间转移车辆的数目 $a=\{-5,-4,...,0,1,...,5\}$，正数代表从门店1移到门店2，负数代表从门店2移到门店1
  3. 衰减系数设为 $\gamma =0.9$

• 我手动实现了这个环境，并且编写了可视化页面，如下
  
  左侧网格显示了所有 20x20 个状态，通过勾选右边控制栏最上面的勾选框，可以查看当前状态价值估计（上图）已经当前策略（下图），通过右边的按钮控制训练过程，其中

  1. 策略评估：执行一步 policy evaluation
  2. 策略提升：执行一步 policy improve，这会导致策略变化
  3. 自动评估：保持策略，不断循环执行 policy evaluation。这时可以从按钮最下面的文本显示观察本次 policy evaluation 后总价值的变化量，看有没有收敛
  4. 策略迭代：同 1.1 节，先自动评估直到总价值的变化量小于阈值（价值收敛），再执行一步策略提升更新策略，循环这个过程直到策略收敛
  5. 价值迭代：原理同 1.2 节，由于价值迭代等价于交替进行单步策略评估和策略提升（详见强化学习笔记（4）第 2.3.5 节），这里直接用这个等价方式实现，提高代码复用性

• 把环境常数整理起来

  import numpy as np
  from scipy import stats
  
  # maximum # of cars in each location
  MAX_CARS = 20
  
  # maximum # of cars to move during night
  MAX_MOVE_OF_CARS = 5
  
  # expectation for rental requests in first location
  RENTAL_REQUEST_FIRST_LOC = 3
  
  # expectation for rental requests in second location
  RENTAL_REQUEST_SECOND_LOC = 4
  
  # expectation for # of cars returned in first location
  RETURNS_FIRST_LOC = 3
  
  # expectation for # of cars returned in second location
  RETURNS_SECOND_LOC = 2
  
  # discount factor
  DISCOUNT = 0.9
  
  # credit earned by a car
  RENTAL_CREDIT = 10
  
  # cost of moving a car
  MOVE_CAR_COST = 2
  
  # An up bound for poisson distribution
  # If n is greater than this value, then the probability of getting n is truncated to 0
  POISSON_UP_BOUND = 11
  
  reqProb1 = stats.poisson.pmf(np.arange(POISSON_UP_BOUND),RENTAL_REQUEST_FIRST_LOC)
  reqProb2 = stats.poisson.pmf(np.arange(POISSON_UP_BOUND),RENTAL_REQUEST_SECOND_LOC)
  reqProb2,reqProb1 = np.meshgrid(reqProb2,reqProb1)
  RENTAL_PROB = np.multiply(reqProb1, reqProb2)  # 请求概率
  
  retProb1 = stats.poisson.pmf(np.arange(POISSON_UP_BOUND),RETURNS_FIRST_LOC)
  retProb2 = stats.poisson.pmf(np.arange(POISSON_UP_BOUND),RETURNS_SECOND_LOC)
  retProb2,retProb1 = np.meshgrid(retProb2,retProb1)
  RETURN_PROB = np.multiply(retProb1, retProb2)  # 归还概率
  

2.1 代码框架

• 这里的代码框架借鉴《边做边学强化学习》中的框架，如下
  
  但是由于这里是 model-based 问题还有 UI，所以不会完全照搬这里。概括讲就是
  1. Environment 类：实现 UI 界面、UI 控制逻辑，重要的是 TD target 也在此计算
  2. Agent 类：实现 UI 控制的相关操作
  3. Brain 类：Agent 对象的成员，主要处理价值估计
• 另外注意到问题包含 4 个泊松分布，环境随机性 $P(s^{\prime },r|s,a)$ 太高，完整计算非常慢，为提升速度，实现时做了两个简化
  1. 设置泊松分布取值上界为 11
  2. 仅保留每天出租请求的两个泊松分布，每天的还车数量直接设置为泊松期望值 3 和 2

2.1 使用 policy iteration 解决

• 标准 policy iteration 伪代码
  
• 实现 policy iteration 的核心代码
  1. Environment 类中 TD target ${\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V(s^{\prime })]$ 的计算代码，使用 numpy 矩阵运算提高效率

     # 当前估计的价值表为 stateValue，计算给定 state 执行 action 的 TD target
     def getValue(self, state, action, stateValue):
         # init return
         returns = 0.0
         returns -= MOVE_CAR_COST * abs(action)
     
         # 可行出借数组
         numOfCarsFirstLoc = int(min(state[0] - action, MAX_CARS))
         numOfCarsSecondLoc = int(min(state[1] + action, MAX_CARS))
     
         # temp
         num1 = np.arange(POISSON_UP_BOUND)
         num2 = np.arange(POISSON_UP_BOUND)
         num2,num1 = np.meshgrid(num2,num1)
     
         # 出借数量矩阵    
         numReq = np.vstack([num2.ravel(), num1.ravel()]).T
         numReq.resize((POISSON_UP_BOUND,POISSON_UP_BOUND,2))
         numReq[numReq[:,:,0]>numOfCarsFirstLoc,0] = numOfCarsFirstLoc
         numReq[numReq[:,:,1]>numOfCarsSecondLoc,1] = numOfCarsSecondLoc
         
         # 获取租金
         reward = np.sum(numReq, axis=2)*RENTAL_CREDIT
     
         # 出租后剩余车数
         num = [numOfCarsFirstLoc,numOfCarsSecondLoc] - numReq
     
         # constantReturnedCars = True 则把还车数量从泊松分布简化为定值
         constantReturnedCars = True
         if constantReturnedCars:         
             # 所有可达新状态
             num += [RETURNS_FIRST_LOC,RETURNS_SECOND_LOC]
             num[num>MAX_CARS] = MAX_CARS
     
             # 新状态价值
             values = stateValue[num[:,:,0],num[:,:,1]]
     
             # 计算收益
             returns += np.sum(RENTAL_PROB * (reward + DISCOUNT * values))
         else:
             # matrix of number of cars returned   
             numRet = np.vstack([num1.ravel(), num2.ravel()]).T
             numRet.resize((POISSON_UP_BOUND,POISSON_UP_BOUND,2))
     
             for returnedCarsFirstLoc in range(0, POISSON_UP_BOUND):
                 for returnedCarsSecondLoc in range(0, POISSON_UP_BOUND):
                     # viable new states
                     num += [returnedCarsFirstLoc,returnedCarsSecondLoc]
                     num[num>MAX_CARS] = MAX_CARS
     
                     # values of viable states
                     values = stateValue[num[:,:,0],num[:,:,1]]
     
                     returns += np.sum(RENTAL_PROB * RETURN_PROB[returnedCarsFirstLoc,returnedCarsSecondLoc]*(reward + DISCOUNT * values))
         return returns
     

  2. Agent 类中的策略迭代相关方法

     # 执行一次策略评估
     def policyEvaluationOneStep(self):
         sumValue_ = self.brain.getSumValue()
         newStateValue = np.zeros((MAX_CARS + 1, MAX_CARS + 1))
         for i,j in self.env.getStateIndex():
             a = self.brain.getPolicy()[i,j]
             newStateValue[i,j] = self.env.getValue([i,j],a,self.brain.getValueTable())
         self.brain.setValueTabel(newStateValue)
     
         valueChanged = abs(self.brain.getSumValue()-sumValue_)
         self.env.updateUILabel('value changed: {}'.format(round(valueChanged,2)))
         self.env.updateUI()
         return valueChanged
         
     # 执行一次策略提升
     def policyImporve(self):
         newPolicy = np.zeros((MAX_CARS + 1, MAX_CARS + 1))
         actions = self.brain.getActions()
         for i, j in self.env.getStateIndex():
             actionReturns = []
             # go through all actions and select the best one
             for a in actions:
                 if (a >= 0 and i >= a) or (a < 0 and j >= abs(a)):
                     q = self.env.getValue([i,j],a,self.brain.getValueTable())
                     actionReturns.append(q)
                 else:
                     actionReturns.append(-float('inf'))
             bestAction = np.argmax(actionReturns)    
             newPolicy[i, j] = actions[bestAction]      
     
         policyChanged = np.sum(newPolicy != self.brain.getPolicy()) != 0
         self.brain.setPolicy(newPolicy)
             
         self.env.updateUILabel('')
         self.env.updateUI()
         return policyChanged
     
     # 反复评估当前策略
     def policyEvaluation(self):
         while self.brain.getAutoExec() == True:
             self.policyEvaluationOneStep()
             time.sleep(self.timeStep)
     
     # 策略迭代算法
     def policyIteration(self):
         policyChanged = True
         while self.brain.getAutoExec() == True and policyChanged:
             # 反复评估直到当前策略下价值收敛
             valueChanged = self.policyEvaluationOneStep()
             while self.brain.getAutoExec() == True and valueChanged > 0.5:
                 valueChanged = self.policyEvaluationOneStep()
                 time.sleep(self.timeStep) 
             # 执行一次策略提升
             policyChanged = self.policyImporve()
     

2.2 使用 value iteration 解决

• value iteration 等价于交替执行单步 policy evaluation 和 policy improve，这样代码可以直接复用上面的

  # 价值迭代算法（等价于 policyImporve 和 policyEvaluationOneStep 交替运行）        
  def valueIteration(self):
      policyChanged = True
      valueChanged = 1
      # 这里我希望手动停止,所以条件中没有 policyChanged
      while self.brain.getAutoExec() == True and valueChanged > 0.5:
          valueChanged = self.policyEvaluationOneStep()
          policyChanged = self.policyImporve()    
          time.sleep(self.timeStep)
  

3. 实验

3.1 收敛结果

• 看一下收敛结果，包括状态价值函数（左）和策略（右），和《Reinforcement Learning An Introduction》中相同
  

3.2 收敛过程

• Policy Iteration 的收敛过程（64倍快放）
  
• Value Iteration 的收敛过程（32倍快放）
  
• 可见 Value Iteration 收敛速度比 Policy Iteration 快很多