【计算机视觉实验】利用均值滤波器、高斯滤波、中值滤波、双边滤波等进行除噪

利用均值滤波器、高斯滤波、中值滤波、双边滤波等进行除噪

一、基本概念

1. 什么是均值滤波器？

        均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中心的周围8个像素，构成一个滤波模板，即包括目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。

        均值滤波也称为线性滤波，其采用的主要方法为邻域平均法。线性滤波的基本原理是用均值代替原图像中的各个像素值，即对待处理的当前像素点（x，y），选择一个模板，该模板由其近邻的若干像素组成，求模板中所有像素的均值，再把该均值赋予当前像素点（x，y），作为处理后图像在该点上的灰度g（x，y），即g（x，y）=∑f（x，y）/m m为该模板中包含当前像素在内的像素总个数。

2. 低通滤波器与高通滤波器？

        前者用于消除噪声，后者用于提取边缘。低通滤波(Low-pass filter) 是一种过滤方式，规则为低频信号能正常通过，而超过设定临界值的高频信号则被阻隔、减弱。但是阻隔、减弱的幅度则会依据不同的频率以及不同的滤波程序（目的）而改变。它有的时候也被叫做高频去除过滤（high-cut filter）或者最高去除过滤（treble-cut filter)。低通过滤是高通过滤的对立。高通滤波器，又称低截止滤波器、低阻滤波器，允许高于某一截频的频率通过，而大大衰减较低频率的一种滤波器。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。

3. 核是什么？

        1) 核表示一个二维大小的矩阵
        2) 核中不同的值可以表示不同的算法，请根据1中介绍的均值滤波器中的核的概念进行推导

4. 应用到的算法+opencv实现
   

5. 均值滤波/盒型模型？

        盒子滤波是一种非常有用的线性滤波，也叫方框滤波，最简单的均值滤波就是盒子滤波归一化的情况。应用：可以说，一切需要求某个邻域内像素之和的场合，都有盒子滤波的用武之地，比如：均值滤波、引导滤波、计算Haar特征等等。优势：就一个字：快！它可以使复杂度为O(MN)的求和，求方差等运算降低到O(1)或近似于O(1)的复杂度，也就是说与邻域尺寸无关了。

        其主要功能是：在给定的滑动窗口大小下，对每个窗口内的像素值进行快速相加求和
        在模式识别领域，Haar特征是大家非常熟悉的一种图像特征了，它可以应用于许多目标检测的算法中。与Haar相似，图像的局部矩形内像素的和、平方和、均值、方差等特征也可以用类似Haar特征的计算方法来计算。这些特征有时会频繁的在某些算法中使用，因此对它的优化势在必行。Boxfilter就是这样一种优化方法，它可以使复杂度为O(MN)的求和，求方差等运算降低到O(1)或近似于O(1)的复杂度，它的缺点是不支持多尺度。。
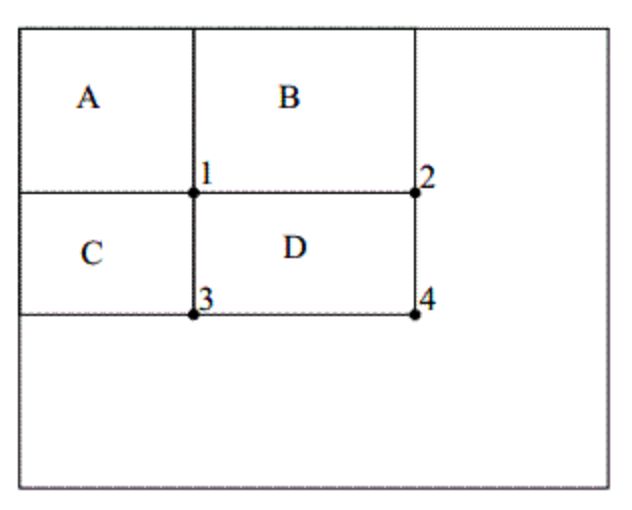
        第一个提出Haar特征快速计算方法的是CVPR2001上的那篇经典论文Rapid Object Detection using a Boosted Cascade of Simple Features ，它提出了integral image的概念，这个方法使得图像的局部矩形求和运算的复杂度从O(MN)下降到了O(4)。它的原理很简单：首先建立一个数组A，宽高与原图像相等，然后对这个数组赋值，每个元素的值A[i]赋为该点与图像原点所构成的矩形中所有像素的和。初始化之后，想要计算某个矩形像素和的时候可以采用如下方法：如图D矩形的像素和就等于A[4] – A[2] – A[3] + A[1]，共4次运算，即O(4)。Integral Image极大的提高了Haar特征的计算速度，它的优点在于能够快速计算任意大小的矩形求和运算。
        Boxfilter的原理有点类似Integral Image，而且比它还要快，但是实现步骤比较复杂。在计算矩形特征之前，Boxfilter与Integral Image都需要对图像进行初始化（即对数组A赋值），不同于Integral Image, Boxfilter的数组A中的每个元素的值是该像素邻域内的像素和（或像素平方和），在需要求某个矩形内像素和的时候，直接访问数组中对应的位置就可以了。因此可以看出它的复杂度是O(1)。

Boxfilter的初始化过程如下：
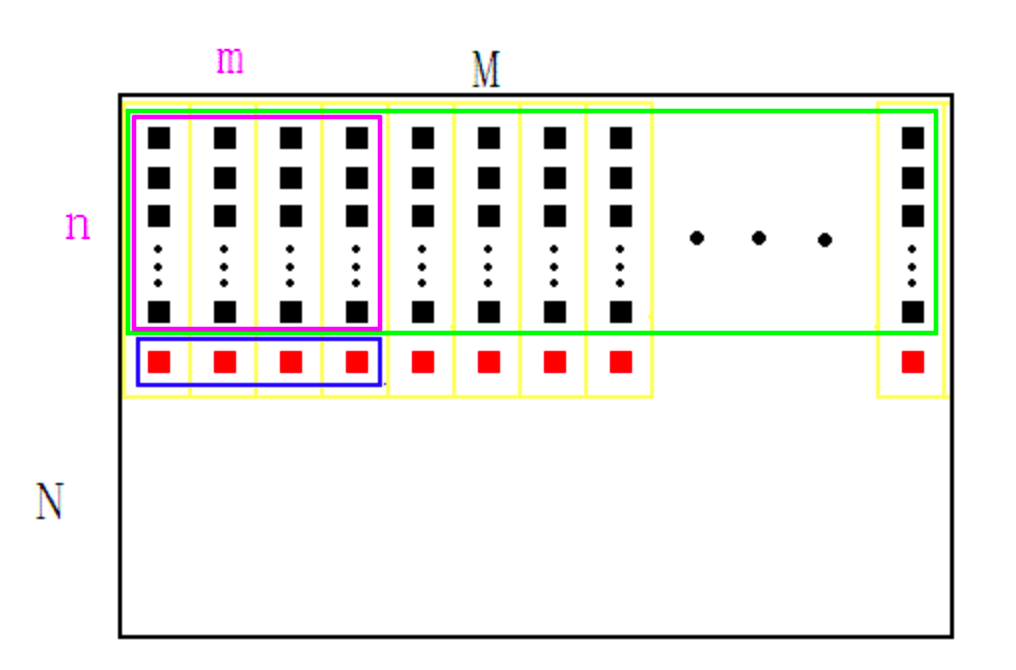
1、给定一张图像，宽高为（M,N），确定待求矩形模板的宽高(m,n)，如图紫色矩形。图中每个黑色方块代表一个像素，红色方块是假想像素。
2、开辟一段大小为M的数组，记为buff, 用来存储计算过程的中间变量，用红色方块表示
3、将矩形模板（紫色）从左上角（0，0）开始，逐像素向右滑动，到达行末时，矩形移动到下一行的开头（0，1），如此反复，每移动到一个新位置时，计算矩形内的像素和，保存在数组A中。以(0,0)位置为例进行说明：首先将绿色矩形内的每一列像素求和，结果放在buff内（红色方块），再对蓝色矩形内的像素求和，结果即为紫色特征矩形内的像素和，把它存放到数组A中，如此便完成了第一次求和运算。
4、每次紫色矩形向右移动时，实际上就是求对应的蓝色矩形的像素和，此时只要把上一次的求和结果减去蓝色矩形内的第一个红色块，再加上它右面的一个红色块，就是当前位置的和了，用公式表示 sum[i] = sum[i-1] - buff[x-1] + buff[x+m-1]
5、当紫色矩形移动到行末时，需要对buff进行更新。因为整个绿色矩形下移了一个像素，所以对于每个buff[i], 需要加上一个新进来的像素，再减去一个出去的像素，然后便开始新的一行的计算了。
        Boxfilter的初始化过程非常快速，每个矩形的计算基本上只需要一加一减两次运算。从初始化的计算速度上来说，Boxfilter比Integral Image要快一些，大约25%。在具体求某个矩形特征时，Boxfilter比Integral Image快4倍，所谓的4倍其实就是从4次加减运算降低到1次，虽然这个优化非常渺小，但是把它放到几层大循环里面，还是能节省一些时间的。对于那些实时跟踪检测算法，一帧的处理时间要严格在40ms以下，正是这些细小的优化决定了程序的效率，积少成多，聚沙成塔。

二、实验代码

import numpy as np
import cv2
import matplotlib.pyplot as plt
########     四个不同的滤波器    #########
img = cv2.imread('cat.jpg')

# 均值滤波
img_mean = cv2.blur(img, (5,5))

# 高斯滤波
img_Guassian = cv2.GaussianBlur(img,(5,5),0)

# 中值滤波
img_median = cv2.medianBlur(img, 5)

# 双边滤波
img_bilater = cv2.bilateralFilter(img,9,75,75)

# 展示不同的图片
titles = ['srcImg','mean', 'Gaussian', 'median', 'bilateral']
imgs = [img, img_mean, img_Guassian, img_median, img_bilater]

for i in range(5):
    plt.subplot(2,3,i+1)#注意，这和matlab中类似，没有0，数组下标从1开始
    plt.imshow(imgs[i])
    plt.title(titles[i])
plt.show()

三、实验结果

1. 对具有高斯噪声的图片进行处理的结果如下。我个人觉得中值最好，其次是高斯。
   
   
2. 对具有椒盐噪声的图片进行处理的结果如下。说实话我觉得中值滤波处理的最好，其次是均值。
   
   

参考资料

[1] 百度百科 https://baike.baidu.com/item/%E4%BD%8E%E9%80%9A%E6%BB%A4%E6%B3%A2

[2] 百度百科 https://baike.baidu.com/item/%E9%AB%98%E9%80%9A%E6%BB%A4%E6%B3%A2%E5%99%A8

[3] 月下花弄影 python+opencv均值滤波，高斯滤波，中值滤波，双边滤波 https://blog.csdn.net/qq_27261889/article/details/80822270

[4] 奇妙的代码之旅 盒式滤波器Box Filter https://www.cnblogs.com/lwl2015/p/4460711.html