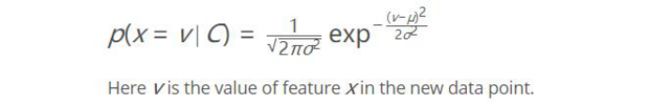自动驾驶算法(一)--基于朴素贝叶斯分类器的汽车行为预测(Linux 下c++工程代码)
因为考虑要交《模式识别》这门课的报告,而且我的研究方向还不是机器学习相关的,所以最近就上网查了些关于自动驾驶汽车中涉及到模式中分类器的相关资料,然后就有了现在这篇文章。一种简单的基于贝叶斯分类器对汽车周围情况的分类预测。你读这篇文章会发现很多都是我个人的见解,由于我不是搞机器学习,所以如果哪里错了请纠正指出。
还是和上一次一样,先给上代码https://github.com/JackJu-HIT/Prediction-self-driving-car-
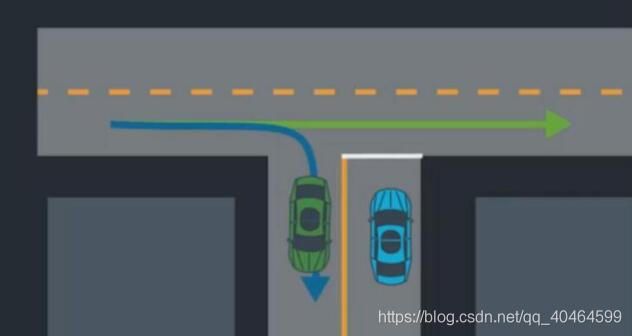
什么是预测,她解决什么问题主要是?设想你是一辆自动驾驶汽车,停留在T型路口,你想要的左转,但是你的传感器发现左侧有俩汽车正在行驶过来。
然后你停留一段时间,作为人类,你可能知道左侧那辆绿色汽车可能做两件事之一即:直走或者右转。
情况1:如果绿色汽车向右转,缓慢行驶,然后你可能意识到,它右转对你来说左转是安全的。成功的预测就是能做出一个安 全、有效的将你送到目的地的决定。如果我们想出绿车的概率分布,我们会看到它是多峰的。
情况2:如果汽车直走,你将会预测它在那个位置。
一般来说我们处理多模态不确定的方式为关于每一种潜在的模态的置信度。首先当汽车从远处走来,有个先验知识概率。
说到这里,我们就知道这个预测是解决啥问题的。
关于预测有两种方法:一是基于数据驱动的方法,一是基于模型预测。
什么叫基于模型预测呢?就是我们通过动力学模型给周围的目标进行建模,这样,当我们的传感器测出他的速度、位置等信息,就能大概算出特征的轨迹,他的优势是能把路上的一些约束条件(交通规则)加进去。
数据驱动算法,就是通过不断的训练,把各种情况都训练到了,他会和人一样去处理。优势是能提取到微小特征。
本文叙述的方法贝叶斯的算法你可以理解为数据驱动方法。
那么我们是这样的一个思路:
我们在路口加一个相机,然后开始记录汽车左转、右转、直行的样本数据,把他统计成样本。然后我们就知道,在这个路口,如果他直走轨迹大概什么样,左拐估计又是什么样子。这就算是已知的即为先验概率。
然后我们的任务是,通过根据输入的目标汽车的信息来与刚才的三种可能性进行比对,就会出现直走、左拐、右拐三个概率,然后选择最大的概率,作为我们认为它下一步最可能的动作。如下图所示,这些就是左拐、直走、右拐的可能轨迹。
那么这些概率应该怎么生成?所以引入了朴素贝叶斯来解决这个问题。这里的贝叶斯使用的高斯分布。
C就是所有可能性,比如你在一个路口,根据经验可知,你只能直走、左转、右转。
所以你要去求解u和sigma的值,分别对用直走、左拐、右拐的三种情况。
换句话说就是你会得到三个P的概率分布对应于直走、左拐、右拐,然后你把某一时刻的信息代入,会给出预测值三个的概率,选择最大的就是我们预测出的行为。
到此,我说完了这个项目的简单思路。提炼一下就是如下两点:
(1)训练 :得到三个P的概率分布对应于直走、左拐、右拐。
(2)预测:使用另一组信息去测试我们这个分类器,然后给出预测结果。
我相信,你研究完这个项目,一定会对机器学习有个很直观的认识,而不是像我之前学习tensorflow时,写的代码都是调用函数(对初学者不友好),形而上学哈,所 以这个项目还是挺适合入门的,是用C++写的。
那么接下来对主要源码进行分析,因为很多我都写了注释,我只分一些关键的吧:
对了,忘介绍了Frenet坐标了,为什么不用笛卡尔坐标系?因为它出的轨迹曲线太复杂。Frenet坐标系是以路面的纵向为s轴,横向为d轴。使用Frenet坐标系描述一个汽车的运行轨迹很方便。
void GNB::train(vector> data, vector labels)
{
/*
Trains the classifier with N data points and labels.
INPUTS
data - array of N observations
- Each observation is a tuple with 4 values: s, d,
s_dot and d_dot.
- Example : [
[3.5, 0.1, 5.9, -0.02],
[8.0, -0.3, 3.0, 2.2],
...
]
labels - array of N labels
- Each label is one of "left", "keep", or "right".
*/
vector> feature_data_left;
vector> feature_data_keep;
vector> feature_data_right;
for (int i=0; i < labels.size(); i++) {
cout << labels[i] << endl;
vector data_input = data[i];
if (labels[i] == "left") add_feature(feature_data_left, data_input);
else
if (labels[i] == "keep") add_feature(feature_data_keep, data_input);
else
if (labels[i] == "right") add_feature(feature_data_right, data_input);
}
left_means = calculate_mean(feature_data_left);
left_stddev = calculate_stddev(feature_data_left, left_means);
keep_means = calculate_mean(feature_data_keep);
keep_stddev = calculate_stddev(feature_data_keep, keep_means);
right_means = calculate_mean(feature_data_right);
right_stddev = calculate_stddev(feature_data_right, right_means);
std::cout<< "\nTraining Complete...\n"<< std::endl;
} 这部分就是训练部分,所谓训练就是通过样本集想求解出三个分布函数的方差和均值。说到这里,还要说一嘴,开头贝叶斯说的很学术,当你究其源码是发现,均值是什么?就是你输入100组数据,只考虑s这一个参数时求均值,其他三个参数同理。方差也一样,想了一下大概是初中的时候学的。具体算法看源码吧,我也写了挺多注释。
tring GNB::predict(vector sample)
{
/*
Once trained, this method is called and expected to return
a predicted behavior for the given observation.
INPUTS
observation - a 4 tuple with s, d, s_dot, d_dot.
- Example: [3.5, 0.1, 8.5, -0.2]
OUTPUT
A label representing the best guess of the classifier. Can
be one of "left", "keep" or "right".
"""
# TODO - complete this
*/
vector prob_classes;
prob_classes.push_back(calculate_prob(sample, left_means, left_stddev));//返回一个数
prob_classes.push_back(calculate_prob(sample, keep_means, keep_stddev));//返回一个数
prob_classes.push_back(calculate_prob(sample, right_means, right_stddev));//发回一个数
//此时,prob_classes有三个数。分别代表[左转的概率,直走的概率,右转的概率]
int idx = 0;
double best_p = 0;
for (int p = 0; p < prob_classes.size(); p++) {
if (prob_classes[p] > best_p) {
best_p = prob_classes[p];
idx = p;
}
}
return possible_labels[idx];//返回最大的概率对应的是索引。
} 这部分就是预测部分了,输入一组数据[s,d,dot(s),dot(d)],然后就会告诉你拥有这个状态汽车会向哪里转向。算出三个概率,选择选择最大的概率,也没啥说的,具体参见代码吧。后面还有些特征添加、均值求解、方差之类的求解思路我都说了,你看代码就行,反正我一开始就是对着代码悟的,因为代码里会告诉你准确的算法实施步骤是则怎样的。
最后一部分就来说说main函数吧.
int main() {
vector< vector > X_train = Load_State("/home/juchunyu/传感器数据融合/gaussian_naive_bayes-master/data/train_states.txt");
vector< vector > X_test = Load_State("/home/juchunyu/传感器数据融合/gaussian_naive_bayes-master/data/test_states.txt");
vector< string > Y_train = Load_Label("/home/juchunyu/传感器数据融合/gaussian_naive_bayes-master/data/train_labels.txt");
vector< string > Y_test = Load_Label("/home/juchunyu/传感器数据融合/gaussian_naive_bayes-master/data/test_labels.txt");
cout << "X_train number of elements " << X_train.size() << endl;
cout << "X_train element size " << X_train[0].size() << endl;
cout << "Y_train number of elements " << Y_train.size() << endl;
GNB gnb ;//= GNB();
gnb.train(X_train, Y_train);
cout << "X_test number of elements " << X_test.size() << endl;
cout << "X_test element size " << X_test[0].size() << endl;
cout << "Y_test number of elements " << Y_test.size() << endl;
/**预测并且与评分**/
int score = 0;
for(int i = 0; i < X_test.size(); i++) {
vector coords = X_test[i];
string predicted = gnb.predict(coords);
if(predicted.compare(Y_test[i]) == 0) {
score += 1;
}
}
float fraction_correct = float(score) / Y_test.size();
cout << "You got " << (100*fraction_correct) << " correct" << endl;
return 0;
} 这里是主程序部分,完成了训练数据的读取、测试数据的读取。然后先调用训练函数,再进行预测。思路很清晰。最后给出了评分函数,对预测的结果进行评价。
写到这里,你就学完了基于朴素贝叶斯预测的分类器的汽车行为预测。(这里提一下,朴素朴素在哪?大家可以思考思考为什么叫朴素贝叶斯?写代码的时候很重要哦)。
如果你觉得我写的还不错,就给我个赞、关注我一下~,如果可以,后续还会更新自动驾驶相关的算法~
20200531
鞠春宇
窗外下雨