目标检测算法——SSD
文章目录
-
-
- 1.SSD简介
- 2.SSD网络结构
-
-
- 1)Backbone
- 2)Default Box
- 3)Predictor
-
- 3.SSD匹配准则
- 4.SSD损失计算
-
-
- 1)类别损失
- 2)定位损失
-
-
1.SSD简介
SSD算法全称是 Single Shot MultiBox Detector,论文链接.
摘要:在PASCAL VOC、COCO和ILSVRC数据集上的实验结果证实,SSD具有与利用额外目标建议步骤的方法竞争的准确性,而且速度快得多,同时为训练和推理提供了统一的框架。对于300×300输入,SSD在VOC2007上实现74.3%的mAP1on测试,在Nvidia Titan X上59 FPS,对于512 × 512输入,SSD实现76.9%的mAP,优于可比的最优秀的Faster R-CNN模型。与其他单级方法相比,SSD即使在较小的输入图像尺寸下也具有更好的精度。
现在的目标检测网络主要分为两类:
1)一类是以Faster RCNN为代表的two step的目标检测网络,因为他需要通过RPN网络去生成系列的目标候选框,然后再针对生成的目标候选框进一步进行概率的预测以及目标边界框的回归。
2)另一类的SSD(及yolo)算法,就是one step的目标检测网络,也就是一步就将目标进行检测出来。
SSD算法是one step算法中的一个比较经典的算法。前面我有做过Faster RCNN的笔记,其重要的问题有:1)对于小目标的检测效果比较差 2)模型大,检测速度比较慢,不能达到实时的效果。
关于Faster RCNN的插曲:
-
1)为什么Faster RCNN中,其对小目标的检测效果会比较差?
这点做FPN结构笔记的时候也有提及到,这是因为Faster RCNN是在比较高维的特征图中进行预测的,而高维的特征图中往往会忽略比较细节的特征信息,只有在比较低维的特征图中这些特征信息才会保留。而比较小的目标的预测主要就是靠这些细节的特征,而因为高维的特征图已经忽视了这些细节,抽象程度越高所保留的细节信息就会越少,所以不可避免的对小目标的检测效果会差,而这也就是为什么Faster RCNN中配合FPN结构的效果会有所提升的一个原因。 -
2)为什么Faster RCNN中,检测速度比较慢?
这是因为其在检测的过程中分了两步走,首先其在RPN这个部分进行了一次预测,然后在Fast RCNN中又进行了一次预测,这就是比较慢的原因,而这也是two steps网络的一个通病。
以下内容,视频的up主是根据pytorch实现的源码中进行讲解的,可能与原paper中实现的方式有所区别。
2.SSD网络结构
1)Backbone
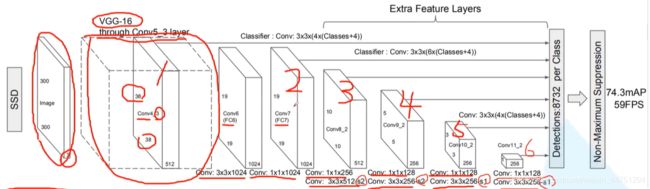
SSD的结构如图所示,可以看见SSD的输入必须是300x300大小的图像,所以会在输入到网络前进行一个缩放。然后会将图像输入到backbone中。可以看见,第一个特征图贯穿到VGG16的中conv5的第三层。
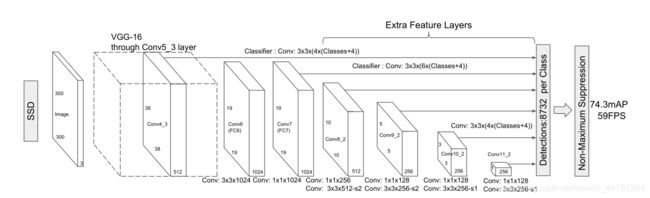
SSD算法的backbone同样是VGG16,以下对照这VGG-16的模型进行理解

- 可以看见,VGG-16中conv5的第三层输出为14x14x512,其中conv4的第三层卷积层,他输出是SSD结构中的第一个预测特征层。
需要注意,原本的VGG中pool5使用的卷积核是2x2,stride为2的,这会将输入的特征矩阵尺度减半,见上图2,14x14x512 ——> 7x7x512;而SSD算法中将其改变为卷积核大小为3x3,stride为1,输入的特征尺度不会减小。所以在SSD结构中,经过conv5_3之后的特征矩阵由原来的38x38x512——>19x19x512之后,经过了pool5,没有改变尺寸,所以还是19x19x512。
然后在此基础上,在后面再添加一系列的卷积操作,得到一系列的预测特征层。
- pool5后,会经过一个3x3的卷积,再经过一个1x1的卷积,得到预测特征层2.输出为19x19x1024
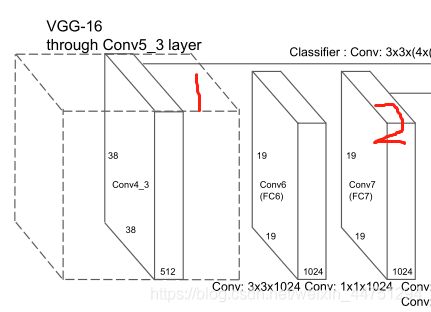
- 然后经过1x1卷积,3x3卷积,得到预测特征层3,输出为10x10x512

- 然后经过1x1卷积,3x3卷积,得到预测特征层4,输出为5x5x256
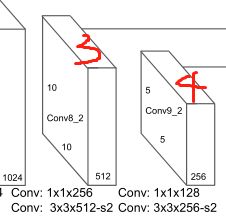
- 然后经过1x1卷积,3x3卷积,得到预测特征层5,输出为3x3x256
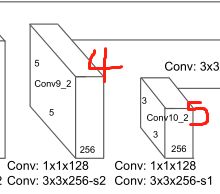
- 然后经过1x1卷积,3x3卷积,得到预测特征层6,输出为1x1x256

所以,会在SSD结构中得到6个预测特征层
需要注意的是,一些3x3的卷积中有些步长是2的,有些步长是1的,当stride=2时,其padding=1;当stride=1时,其padding=0.这些细节需要注意。
此后,会在这6个特征层中分别预测不同大小的目标。比如在第一层的预测特征层中,会让其预测相对较小的目标;而随着抽象程度加深,会让其检测相对较大的目标。

比如如图左边一幅标注好的图像,在右边有两个特征矩阵,一个8x8的特征矩阵,一个4x4的特征矩阵,这个8x8的特征矩阵相比4x4的特征矩阵的抽象程度会更低,也就是保留的细节信息会更多一些。那么会在相对底层的特征矩阵上预测较小的目标,在原图当中猫的面积相对狗的面积要小,所以猫会在8x8的特征矩阵上预测其目标边界框。而在4x4的特征层中适合检测原图中狗的目标。这样就实现了在不同的特征图上预测匹配不同尺寸的目标,这样可以提升小目标的检测效果。
这里的default Box与Faster RCNN中的anchor box是类似的
2)Default Box
Default Box中关于scale与aspect的设定,原文中有给定数学公式:

但是据视频中的up讲到,如果根据这个公式去计算,与github上是一些SSD算法的实现是不一样的,所以这里忽略这个公式,直接看尺度与目标比例。
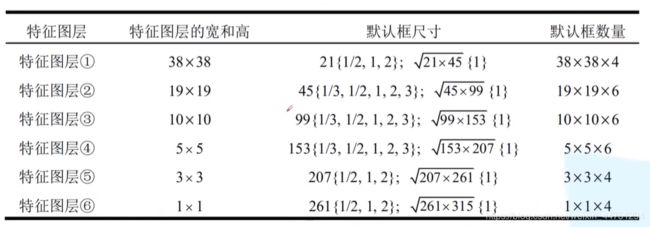
分析:
- 对于预测特征层1,5,6有3种比例:{1:2,1:1,2:1},所以会有4个default Box。而对于预测特征层2,3,4有5种比例:{1:2,1:3,1:1,2:1,3:1},所以会有6个default Box。
- 这里的4个default Box与6个default Box其实是每种比例构成的default Box,再加上一个由sk’=√sksk+1,构成的1:1的default Box。所以对于预测特征层1,5,6,3+1=4个default Box。对于预测特征层2,3,4,5+1=6个default Box。
这里给出视频up整理出的scale参数与aspect参数:
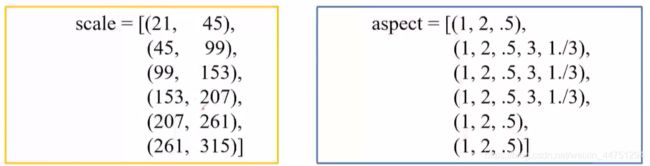
Default Box的总数量计算:
38x38x4 + 19x19x6 + 10x10x6 + 5x5x6 + 3x3x4 + 1x1x4 = 8732
所以,在SSD结构中,一共会生成8732个Default Box。
为了进一步的便于理解,up主还弄了一张照片,我以此进一步作解释
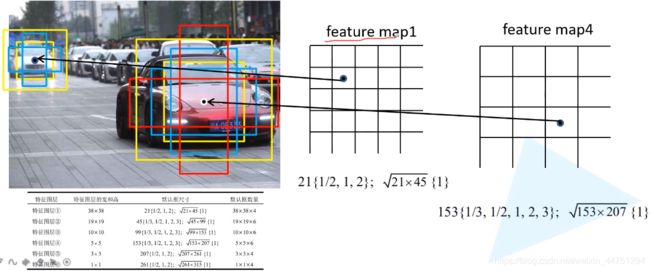
这里以预测特征层1和预测特征层4为例:
1)对于预测特征层1
根据我们刚刚看见的那个表格,预测特征层1是有3种尺寸的,分别是:{1:1,1:2,2:1}对应着有4个default box。如图所示,由于预测特征层1是比较底层的特征层,所以会预测一些比较小的目标,可以看见远侧的小车周围有4个default box围住。
2)对于预测特征层4
根据我们刚刚看见的那个表格,预测特征层4是有5种尺寸的,分别是:{1:1,1:2,1:3,2:1,3:1}对应着有6个default box。如图所示,由于预测特征层4是比较高层的特征层,所以会预测一些比较大的目标,可以看见近处的小车周围有6个default box围住。
如果将我们6个特征图上每一个位置上的default box都绘制在图片上(也就是一副图像上会有8k多个default box),基本上是可以覆盖图片上所有出现的目标的。
3)Predictor

对于大小为m × n且有p个通道的特征层,预测潜在检测参数的基本元素是一个3 × 3 × p的小核,它产生一个类别得分,或者一个相对于默认框坐标的形状偏移。也就是通过3x3的卷积层来预测类别概率与边界框回归参数。

具体来说,对于给定位置的k中的每一个方框,我们计算c类得分和相对于原始默认方框形状的4个偏移量。这就产生了(c + 4)k个卷积核,这些卷积核被应用在特征层的每个位置,对于一个m × n 特征图会产生(c + 4)kmn输出。
简单来说:
就是对于每一层特征层上的每一个default box都需要预测其属于c类中的哪一类(这里的c是包括的背景个数的,想piscal voc中的c就是20+1类),c中额每一个值就是对应了是改类别的概率,还需要预测其边界框回归参数的偏移量,所以就是(c + 4)* k 个卷积核。
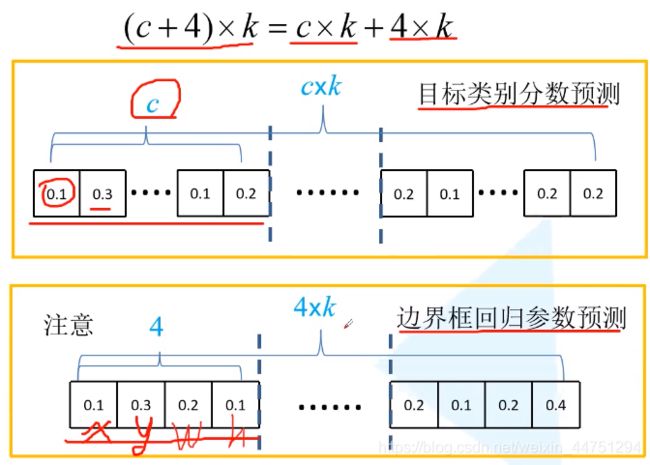
(需要注意的是,在讲Faster RCNN时,在讲生成边界框回归参数数时,会生成 4 x c个边界框回归参数,也就是会针对我们每一个anchor,分别去生成针对每一个类别的边界框回归参数。)
3.SSD匹配准则
- 1)对于每一个ground truth去匹配与他的IoU值最大的defult box,标记为正样本;
- 2)对于defult box与任意的ground truth的IoU>0.5,也标志为正样本
负样本:
如果把正样本以外的都归类为负样本,会导致样本不平衡的问题。因为一般来,对于一张图像的正样本只有十来个defult box。

SSD中没有使用所有的负面例子,而是使用每个默认框的置信度损失最高的值对它们进行排序(因为对于负样本的置信度越高说明网络预测的错误更加离谱),并选择最上方的值,这样负面和正面的比率最多为3:1。
4.SSD损失计算
SSD中的损失包括类别损失与定位损失

其中:N为匹配到的正样本个数,α为平衡系数,可以直接取1
1)类别损失
类别损失也包括两类:
1)正样本的类别损失(第一项)
2)负样本的类别损失(第二项)

对于正样本的损失,其实就是一个Softmax loss;p代表的是类别,p=0表示的是背景。所以对于负样本的损失只需要关注p=0就可以了。
2)定位损失
定位损失是只针对正样本而言的,因为负样本连ground truth都没有,所以无法计算其的一个定位损失,而且计算也没有任何的意义。

这里的定位损失其实也就是Faster RCNN的边界框回归损失,计算都是类似的。
其中,g^ jm 的计算公式为:

- gjcx 表示:ground truth box中心点的x坐标
- gjw 表示:ground truth box的宽度
- dicx 表示:第i个default box中心点的x坐标
- diw 表示:第i个default box的宽度
- (其他的类似)
最后,进行一个回顾:

首选对backbone输入一张300x300的图像,然后首先通过VGG16的前置网络部分(直到pool5,只不过pool5没有改变图像的尺寸),然后依次通过其他的卷积层处理之后得到了6个预测特征层。然后对每一个预测特征层上的每一个点生产预设数目的default boxs,预测不同比例以及尺度的目标,然后对这些default box进行辩解框调整。这是同每个预测特征层后增加一个3x3的卷积核训练得到的。调整好位置的default box一共有8k多个,然后通过极大值抑制算法去挑选一些比较好的default box,从而达到了预测的效果。
参考资料:
https://www.bilibili.com/video/BV1fT4y1L7Gi
https://arxiv.org/abs/1512.02325
