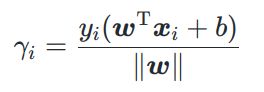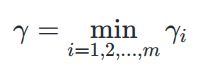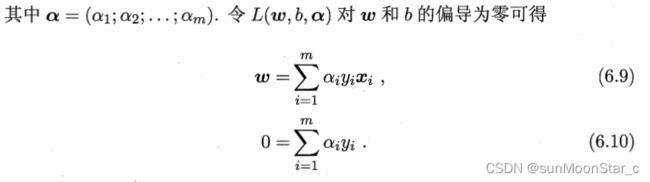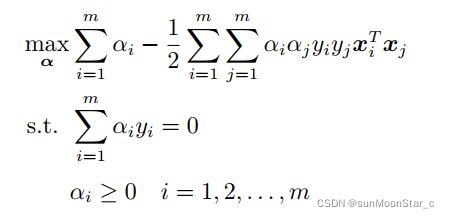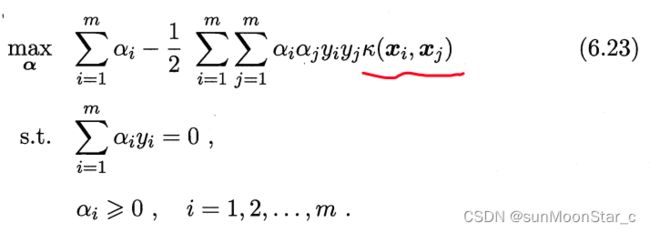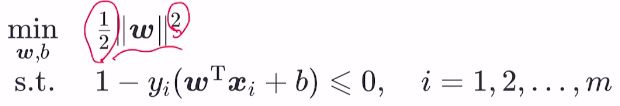机器学习西瓜书笔记：支持向量机SVM（support vector machines）
一、概念
支持向量机
分类学习的基本思想：基于训练样本集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . . , ( x m , y m ) } , y i ∈ { − 1 , + 1 } D = \{(x_1,y_1),(x_2,y_2),....,(x_m,y_m)\}, yi∈\{-1,+1\} D={(x1,y1),(x2,y2),....,(xm,ym)},yi∈{−1,+1}，在样本空间找到一个划分超平面，将不同类别样本分开
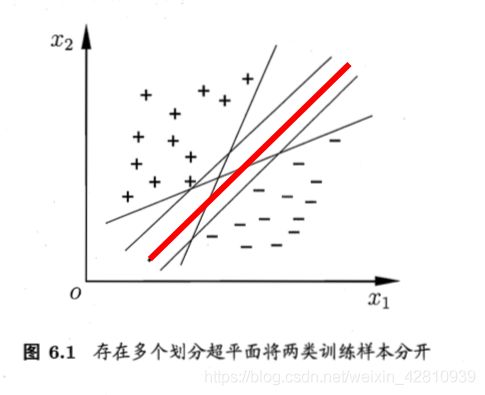
支持向量机：分类问题，对于线性可分的数据集，找距离正负样本都最远的超平面模型。（感知机的超平面解可能不唯一，但是SVM解是唯一的）
- 位于两类样本正中间的，对训练样本局部扰动的容忍性最好，产生的分类结果最健壮（robust），对未见示例的泛化能力最强。
对于泛化能力最强的解释：
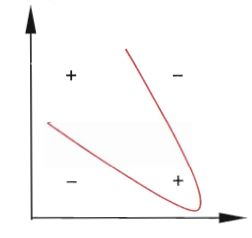
如图，如果我们选择的超平面是红色，他距离正负样本的距离不是都是最远，则对于新的正样本（紫色），会把它划分到负样本中，即泛化能力不强。
而SVM找到的超平面是绿色，明显泛化能力更好，分类错误情况更少。
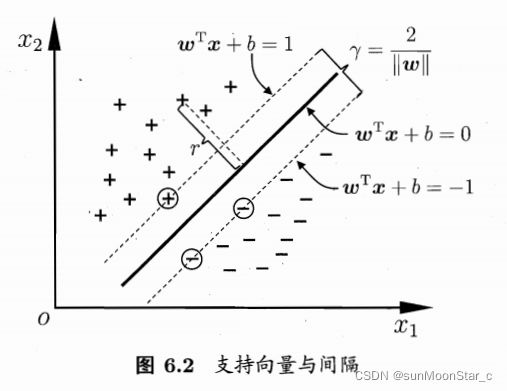
支持向量support vector
距离超平面最近的训练样本点
超平面 w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x} + b= 0 wTx+b=0
超平面方程和性质
1、超平面方程： w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x} + b= 0 wTx+b=0（回忆神经网络时b是 − θ -\theta −θ阈值）
- n=1，超平面是一个点
- n=2，超平面是一条直线
- n=3，超平面是一个面
- …
超平面可记为 ( w ⃗ , b ) (\vec{w}, b) (w,b)
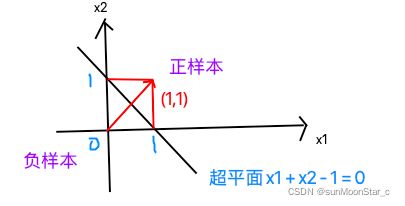
2、超平面性质：以n=2时， w 1 = w 2 = 1 , b = − 1 w_1 = w_2 = 1, b= -1 w1=w2=1,b=−1超平面为例
- 超平面方程不唯一，每一项添加一个系数，结果还是一样
- 法向量 w ⃗ \vec{w} w垂直于超平面：如图法向量 w ⃗ = ( w 1 , w 2 ) = ( 1 , 1 ) \vec{w} = (w_1,w_2) = (1,1) w=(w1,w2)=(1,1)，决定超平面的方向
- 法向量 w ⃗ \vec{w} w，和位移项 b b b，确定一个唯一的超平面
- 法向量 w ⃗ \vec{w} w指向的一半为正空间，另一半为负空间。
- 正空间内的点，带入 w ⃗ T x ⃗ + b > 0 \vec{w}^T\vec{x} +b > 0 wTx+b>0
- 负空间内的点，带入 w ⃗ T x ⃗ + b < 0 \vec{w}^T\vec{x} +b < 0 wTx+b<0
- 超平面上的点，带入 w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x} +b = 0 wTx+b=0
样本点到超平面的距离：几何间隔的一部分
样本空间中任意点 x ⃗ \vec{x} x 到超平面 ( w ⃗ , b ) (\vec{w}, b) (w,b)的距离 r r r
该公式其实想一下对于直线 A x + B y + C = 0 Ax + By + C=0 Ax+By+C=0,平面上任意一点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)到直线的距离公式是： ∣ A x 0 + B x 0 + C ∣ A 2 + B 2 {|Ax_0 + Bx_0+C|}\over {\sqrt{A^2+B^2}} A2+B2∣Ax0+Bx0+C∣即可对应 n 维 n维 n维空间公式。
具体推导过程：
几何间隔margin：不按照西瓜书
西瓜书对于间隔的定义：
间隔margin：两个异类支持向量 到超平面的距离之和
该公式跳了很多步骤，西瓜书会对正确分类的SVM超平面模型假设为6.3，这里的+1，-1其实可以是任意常数，对结果w，b不影响，因为系数可以缩放。
这里规定是+1，-1，也就决定了支持向量到超平面距离=1，则异类支持向量到超平面距离之和就如6.4所示。
后面的推导，没有先假设是+1，-1，而是到了最后一步，令分子=1，反正就是这些系数全都可以为了计算随意设置，不影响求w和b
非西瓜书
1、数据集中的样例点 ( x i ⃗ , y i ) , y i ∈ { − 1 , 1 } , i = 1 , 2 , . . , m (\vec{x_i}, y_i), y_i \in \{-1,1\},i=1,2,..,m (xi,yi),yi∈{−1,1},i=1,2,..,m关于超平面 w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x} + b= 0 wTx+b=0几何间隔 γ i \gamma_i γi：
几何间隔不仅能体现真实间隔大小，即样本点到超平面的距离r，还能体现分类是否正确
- 分类正确时，几何间隔 γ i > 0 \gamma_i > 0 γi>0
- 分类错误时，几何间隔 γ i < 0 \gamma_i <0 γi<0
证明：
- 正空间内的点，带入 w ⃗ T x ⃗ + b > 0 \vec{w}^T\vec{x} +b > 0 wTx+b>0
- 分类错误：真实标记 y i = − 1 y_i=-1 yi=−1，则 γ i \gamma_i γi<0
- 分类正确：真实标记 y i = 1 y_i=1 yi=1，则 γ i \gamma_i γi>0
- 负空间内的点，带入 w ⃗ T x ⃗ + b < 0 \vec{w}^T\vec{x} +b < 0 wTx+b<0
- 分类错误：真实标记 y i = 1 y_i=1 yi=1，则 γ i \gamma_i γi<0
- 分类正确：真实标记 y i = − 1 y_i=-1 yi=−1，则 γ i \gamma_i γi>0
- 超平面上的点，带入 w ⃗ T x ⃗ + b = 0 \vec{w}^T\vec{x} +b = 0 wTx+b=0
2、数据集 X X X 到超平面的几何间隔：定义为 X X X中所有样本点的几何间隔的最小值
二、SVM
1、模型：实现分类的最大间隔超平面
我们直接规定该超平面是正确分类的，分类功能套个sign函数，把实值变为分类值1，-1.
-
当前数据集线性可分，代表我们必然能找到能正确划分的超平面，也就是我们最优化间隔过程结束后，找到的最大的 γ \gamma γ必然是>0的。
-
因此一开始我们应当规定超平面模型就是正确分类的模型，没必要考虑无法正确分类，因为对于线性可分数据集不可能。
接下来就是对这个能正确分类的超平面，使其损失函数最小化，也就是间隔最大化。
2、策略：推导损失函数
最终目的：SVM要求一个超平面 γ \gamma γ，该超平面的几何间隔是所有超平面中最大的。
同时几何间隔自身要满足约束条件： γ = min γ i \gamma = \min \gamma_i γ=minγi，即是数据集中样本点到超平面距离的最小值。
首先回忆样本点到超平面的间隔公式：
SVM问题转化为：
这里的(xmin,ymin)就是西瓜书定义的支持向量
分母相同，去掉，问题变为：
求最优解需要限制 ( w ⃗ ∗ , b ) (\vec{w}^*, b) (w∗,b)
在求解之前还要继续变化问题形式，直到是一个可以求出固定最优解的最小化问题
求能得到最大几何间隔的最优解 ( w ⃗ ∗ , b ) (\vec{w}^*, b) (w∗,b)。
但是此条件极值问题，和LDA中一样，无法直接求解。
因为假设最优解为 ( w ⃗ ∗ , b ) (\vec{w}^*, b) (w∗,b)，则 ( α w ⃗ ∗ , α b ) (\alpha\vec{w}^*,\alpha b) (αw∗,αb)必然也是最优解，会上下约分掉。
因此必须对 ( w ⃗ ∗ , b ) (\vec{w}^*, b) (w∗,b)做出限制：通常是固定分子或者分母为一个固定常数值。不固定的话，系数 α \alpha α随便取了，无法求解；固定的话，就必须存在唯一一个 α \alpha α满足此等式。
SVM固定分子：相当于规定支持向量距离超平面1
问题转化为：
最大化问题转最小化问题
通常把最大化问题转化为最小化问题，毕竟是叫损失函数，则把max的变成其倒数，约束写成<=0的形式。
而为了后面计算，如求导方面，写成 1 2 {1\over 2} 21模长的平方。
最优化主问题为：
3、求解：转化为拉格朗日对偶问题
3.1、主问题：其实本身已经是凸优化问题
该主问题满足：
- 是凸优化问题
- 具有强对偶性：则对偶问题的最优解就是主问题的最优解。证明见后面
因此虽然主问题本身已经是凸优化问题，有现成优化计算包求解，但是转化为对偶问题求解更加高效。
3.2、拉格朗日函数：
对m条不等式约束添加拉格朗日乘子 α i \alpha_i αi，对偶问题要求 α i ≥ 0 \alpha_i \ge 0 αi≥0
3.3、求解对偶函数 Γ ( α ⃗ ) \Gamma(\vec{\alpha}) Γ(α) = inf L ( w ⃗ , b , α ) ⃗ \inf L(\vec{w}, b,\vec{\alpha)} infL(w,b,α)
也就是求L的最小值，求L最小值为啥我们求偏导=0呢？有如下几种理解：
- 凸函数的性质：该拉格朗日函数把w,b变成 w ⃗ ^ \hat{\vec{w}} w^，是关于 w ⃗ ^ \hat{\vec{w}} w^的凸函数，则对其求偏导=0，解出来的一定是最优解。
- 该SVM问题强对偶性成立，则主问题的最优解必然满足5个KKT条件，条件一就是拉格朗日函数的最优解带入偏导数=0
矩阵，向量求偏导常用公式：
带入偏导=0，得到对偶函数 Γ ( α ⃗ ) \Gamma(\vec{\alpha}) Γ(α) = inf L ( w ⃗ , b , α ) ⃗ \inf L(\vec{w}, b,\vec{\alpha)} infL(w,b,α)为：
3.4 对偶问题
对偶问题的定义
这里给出简单定义，后面有详细讲解
SVM的对偶问题：6.11
有了对偶函数，根据对偶问题需要的约束条件 α i ≥ 0 \alpha_i \ge 0 αi≥0，以及题目本身需要的约束，得到对偶问题
强对偶性成立还需要满足KKT条件
KKT条件见后面讲解
3.5 求解6.11对偶问题
后面再讲
将样本从低维映射到高维。
则高维的划分超平面模型为：
对偶问题变为：
问题：原始样本映射到的高维特征空间，可能维数特别大，甚至是无穷维，则计算6.21 ϕ ( x ⃗ i ) T p h i ( x ⃗ i ) \phi(\vec{x}_i)^Tphi(\vec{x}_i) ϕ(xi)Tphi(xi)会很困难。
解决：引入核函数 κ ( ⋅ , ⋅ ) \kappa(·,·) κ(⋅,⋅)
该核函数，把原本高维内积问题变成：在原始样本维度上做内积
6.21对偶问题重写为：求出使得对偶问题最大化的核函数值
需要求解的超平面模型为：
- 根据6.9： w ⃗ = ∑ i = 1 m α i y i ϕ ( x ⃗ i ) \vec{w} = \sum_{i=1}^m\alpha_i y_i \phi(\vec{x}_i) w=∑i=1mαiyiϕ(xi)
支持向量展式（support vector expansion）
6.24表示：超平面模型的最优解，可以通过训练样本 x ⃗ \vec{x} x的核函数展开
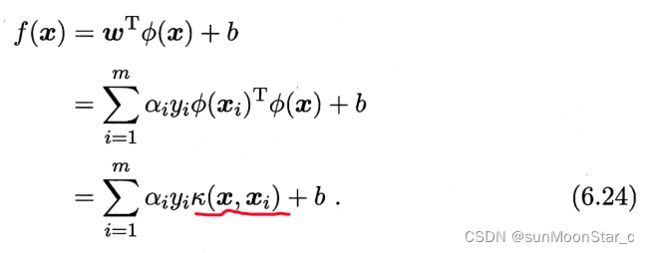
则只要知道了核函数，就能求出超平面模型。
核函数的选取需要满足两个条件，见附录。
常用核函数如下：都满足核函数定理
选取一个合适的核函数，映射到合适的特征空间，求出性能佳的划分超平面模型。
公式推导过程：
附录1：凸优化问题
凸函数：海塞矩阵是正定或者半正定
凸优化问题：
- 目标函数是凸函数
- 约束集合是凸集
特别地：如下情况也是凸优化问题
1、目标函数是凸函数
2、约束集合是凸集
3、不等式约束函数是凸函数
4、等式约束函数是线性函数
显然SVM是个凸优化问题。
附录2：针对任意优化问题：转化为对偶问题dual problem
不管你主问题是不是凸优化问题，其对偶问题必然是凸优化问题
1、一般的优化问题：即不一定是凸优化问题
1、形式
2、该优化问题的 定义域 D D D 为是每个函数定义域的交集：
3、可行集 D ~ \tilde{D} D~： 即定义域中能满足约束条件的
4、最优值 p ∗ = min { f ( x ~ ⃗ ) } p^* = \min\{f(\vec{\tilde{x}})\} p∗=min{f(x~)}, x ~ ⃗ ∈ D ~ \vec{\tilde{x}} \in \tilde{D} x~∈D~，即被优化函数 符合约束条件时（可行集上） 的最小值
2、一般优化问题的拉格朗日函数
3、拉格朗日对偶函数 Γ ( μ ⃗ , λ ⃗ ) \Gamma(\vec{\mu}, \vec{\lambda}) Γ(μ,λ)
下确界：简单理解为下界。记为 i n f ( f ( x ) ) inf(f(x)) inf(f(x))
- 如 f ( x ) = e x f(x) = e^x f(x)=ex， i n f ( f ( x ) ) = 0 inf(f(x)) = 0 inf(f(x))=0
- f无下界， i n f ( f ( x ) ) = − ∞ inf(f(x)) = -\infin inf(f(x))=−∞
定义优化问题的 拉格朗日对偶函数 Γ ( μ ⃗ , λ ⃗ ) \Gamma(\vec{\mu}, \vec{\lambda}) Γ(μ,λ)为：拉格朗日函数 L ( x ⃗ , μ ⃗ , λ ⃗ ) L(\vec{x}, \vec{\mu}, \vec{\lambda}) L(x,μ,λ)在 D D D上的下确界：
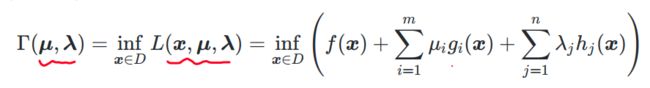
对偶函数的2个性质：
性质2证明：
- 最优值 p ∗ = min { f ( x ~ ⃗ ) } p^* = \min\{f(\vec{\tilde{x}})\} p∗=min{f(x~)}, x ~ ⃗ ∈ D ~ \vec{\tilde{x}} \in \tilde{D} x~∈D~，即被优化函数 符合约束条件时（可行集上） 的最小值
- 可行集 D ~ \tilde{D} D~：即定义域中能满足约束条件的
1、证明 Γ ( μ ⃗ , λ ⃗ ) ≤ p ∗ \Gamma(\vec{\mu}, \vec{\lambda}) \leq p^* Γ(μ,λ)≤p∗，即证： Γ ( μ ⃗ , λ ⃗ ) ≤ min { f ( x ~ ⃗ } ) \Gamma(\vec{\mu}, \vec{\lambda}) \leq \min\{f(\vec{\tilde{x}}\}) Γ(μ,λ)≤min{f(x~})；即证： Γ ( μ ⃗ , λ ⃗ ) ≤ f ( x ~ ⃗ ) \Gamma(\vec{\mu}, \vec{\lambda}) \leq f(\vec{\tilde{x}}) Γ(μ,λ)≤f(x~)
2、即证: inf x ⃗ ∈ D L ( x ⃗ , μ ⃗ , λ ⃗ ) ≤ f ( x ~ ⃗ ) \inf_{\vec{x} \in D} L(\vec{x}, \vec{\mu}, \vec{\lambda}) \leq f(\vec{\tilde{x}}) infx∈DL(x,μ,λ)≤f(x~)。
- 左边是拉格朗日函数全局定义域上符合约束条件的下界，肯定比更小定义域范围的可行集上的函数值更小，则 inf x ⃗ ∈ D L ( x ⃗ , μ ⃗ , λ ⃗ ) ≤ L ( x ⃗ ~ , μ ⃗ , λ ⃗ ) \inf_{\vec{x} \in D} L(\vec{x}, \vec{\mu}, \vec{\lambda}) \leq L(\tilde{\vec{x}}, \vec{\mu}, \vec{\lambda}) infx∈DL(x,μ,λ)≤L(x~,μ,λ)
3、即证 L ( x ⃗ ~ , μ ⃗ , λ ⃗ ) ≤ f ( x ~ ⃗ ) L(\tilde{\vec{x}}, \vec{\mu}, \vec{\lambda}) \leq f(\vec{\tilde{x}}) L(x~,μ,λ)≤f(x~):
- 根据可行集上的点符合约束条件的而行之，很容易就能证明
证明过程倒推即可。
4、拉格朗日对偶问题：恒为凸优化问题；求对偶函数最大值
原优化问题称为：主问题
拉格朗日对偶问题：注意拉格朗日参数要求都>=0
定义就是求对偶函数最大值的优化问题！！
对偶问题恒为凸优化问题
5、强对偶性：解释为啥SVM是凸优化问题还用对偶问题求解
- 首先SVM问题强对偶性成立，因此对偶问题的最优解（求最大值）就是原问题（求最小值）的最优解。也就是说是可以求解
- 对偶问题的参数是拉格朗日乘数，和样本量m成正比。而原问题和特征向量的维数n成正比。一般维数n远大于样本量m，此时用对偶问题求解更高效。
之前证明了对偶函数的性质2：
μ ⃗ ≽ 0 时 ， Γ ( μ ⃗ , λ ⃗ ) ≤ p ∗ = min { f ( x ⃗ ~ ) } \vec{\mu} \succcurlyeq 0时，\Gamma(\vec{\mu}, \vec{\lambda}) \leq p^* = \min\{f(\tilde{\vec{x}})\} μ≽0时，Γ(μ,λ)≤p∗=min{f(x~)}
把对偶问题的最优值记为： d ∗ = max { Γ ( μ ⃗ , λ ⃗ ) } ≤ p ∗ d^* = \max\{\Gamma(\vec{\mu}, \vec{\lambda})\} \leq p^* d∗=max{Γ(μ,λ)}≤p∗。此时称为弱对偶性成立
当 d ∗ = p ∗ d^* = p^* d∗=p∗时，称为强对偶性成立
何时强对偶性成立？显然SVM成立
- SVM的主问题是凸优化问题
- 且可行集中存在一点能使得 所有不等式约束的不等号成立
附录3：KKT条件：5个（强对偶性成立时需要满足）
SVM强对偶性成立，则必然满足入五个条件：
- x ⃗ ∗ \vec{x}^* x∗：主问题的最优解
- ( μ ⃗ ∗ , λ ⃗ ∗ ) (\vec{\mu}^*, \vec{\lambda}^*) (μ∗,λ∗)：对偶问题的最优解
最优解必须满足：
- 对参数求偏导=0：拉格朗日乘数法就满足了
- 等式约束成立
- 不等式约束成立
- 不等式约束的m个拉格朗日乘数必须>=0
- 不等式约束的拉格朗日乘数*不等式约束 = 0
附录4：核函数
问题：原始维度的样本空间内，不存在一个能正确划分两类样本的超平面
如：异或问题
解决：把样本 x ⃗ \vec{x} x映射到更高维的特征空间，映射后的样本为 ϕ ( x ⃗ ) \phi(\vec{x}) ϕ(x)。样本在此高维特征空间内线性可分。（原始空间时有限维，即属性有限，则必然存在一个高位特征空间使得样本线性可分）
二维特征空间，映射到三维特征空间。找到划分超平面
核函数 κ \kappa κ和映射 ϕ \phi ϕ是一一对应的，已知一个，就能求出另一个。
核函数的形式不能随意取，需要满足一定条件
高斯核函数
我们知道了若满足上述两个条件，核函数则能写成向量内积形式。
虽然依然不知道如何求出 ϕ \phi ϕ映射函数的形式。但是可以求出 w ⃗ T ϕ ( x ⃗ ) + b \vec{w}^T\phi(\vec{x})+b wTϕ(x)+b，则模型有了，样本也可以划分类别了