自编码器AutoEncoder解决异常检测问题

一、 自编码器（Auto-Encoder）介绍

1. AE算法的原理

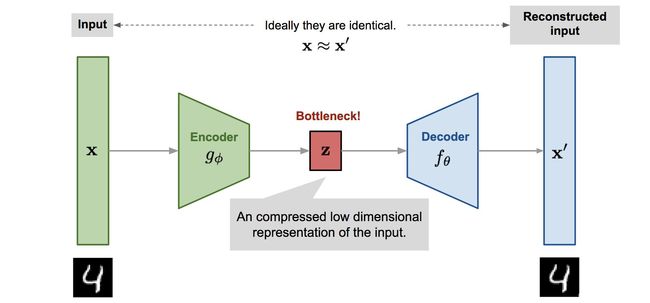
Auto-Encoder，中文称作自编码器，是一种无监督式学习模型。它基于反向传播算法与最优化方法（如梯度下降法），利用输入数据 $X$ 本身作为监督，来指导神经网络尝试学习一个映射关系，从而得到一个重构输出 $X^R$ 。在时间序列异常检测场景下，异常对于正常来说是少数，所以我们认为，如果使用自编码器重构出来的输出 $X^R$ 跟原始输入的差异超出一定阈值（threshold）的话，原始时间序列即存在了异常。

通过算法模型包含两个主要的部分：Encoder（编码器）和Decoder（解码器）。

编码器的作用是把高维输入 $X$ 编码成低维的隐变量 $h$ 从而强迫神经网络学习最有信息量的特征；解码器的作用是把隐藏层的隐变量 $h$ 还原到初始维度，最好的状态就是解码器的输出能够完美地或者近似恢复出原来的输入, 即 $X^R$ $\approx X$ .

如图所示，

(1)从输入层 ->隐藏层的原始数据X的编码过程：
$$h=g{\theta }_1(x)=\sigma (W_{1}x+b_1)$$

(2)从隐藏层 -> 输出层的解码过程：
$$\hat{x}=g{\theta }_2(h)=\sigma (W_{2}x+b_2)$$

那么算法的优化目标函数就写为：$MinimizeLoss=dist(X,X^R)$
其中 $dist$ 为二者的距离度量函数，通常用 MSE（均方方差）

2. AE算法的作用

自编码可以实现类似于 PCA 等数据降维、数据压缩的特性。从上面自编码的网络结构图，如果输入层神经元的个数 n 大于隐层神经元个数 m，那么我们就相当于把数据从 n 维降到了 m 维；然后我们利用这 m 维的特征向量，进行重构原始的数据。这个跟 PCA 降维一模一样，只不过 PCA 是通过求解特征向量，进行降维，是一种线性的降维方式，而自编码是一种非线性降维。自编码器常用于异常检测和状态检测。

3. AE算法的优缺点

优点：泛化性强，无监督不需要数据标注

缺点：针对异常识别场景，训练数据需要为正常数据。

二、 自编码器AutoEncoder解决异常检测问题（手把手写代码）

1. 关于数据集准备

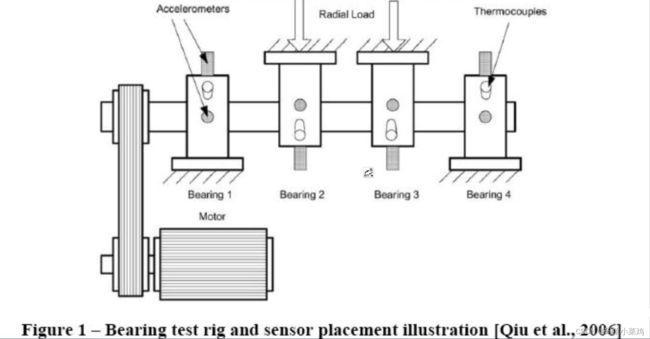
从NASA声学和振动数据库下载数据集。
点击直达Kaggle官网
点击直达百度网盘链接：

原始数据集中包含三组测试，每组测试都是包含很多文件，这些文件都是10分钟的数据量（测试1略有例外），采样周期为1s，采样率设置为20 kHz，所以每个文件由20480点组成。文件名为采集数据的起始时间戳，数据文件中的每个记录（行）是一次采样点，每一列表示一个测试通道（NI采集的卡的测试通道）。

载入数据集

# Import libraries, core libraries are numpy and sklearn
import os
import pandas as pd
import numpy as np
import tensorflow as tf
from sklearn import preprocessing
import seaborn as sns
sns.set(color_codes=True)
import matplotlib.pyplot as plt
# sns.axes_style("white")
# sinplot()
# sns.despine()

# Load data set
folder = r'C:\Users\EliYu\Downloads\archive\2nd_test'
data_dir = folder+'\\2nd_test'
merged_data = pd.DataFrame()

for filename in os.listdir(data_dir):
#     print(filename)
    dataset = pd.read_csv(os.path.join(data_dir, filename), sep='\t')
    dataset_mean_abs = np.array(dataset.abs().mean())
    dataset_mean_abs = pd.DataFrame(dataset_mean_abs.reshape(1,4))
    dataset_mean_abs.index = [filename]
    merged_data = merged_data.append(dataset_mean_abs)
merged_data.reset_index(inplace=True)  # reset index to get datetime as columns

# 将原始数据集聚合为单个csv文件
merged_data.columns = ['Datetime','Bearing 1','Bearing 2','Bearing 3','Bearing 4'] # rename columns
merged_data.sort_values(by='Datetime',inplace=True)
merged_data.to_csv('2nd_test_resmaple_10minutes.csv')

# 读取数据集
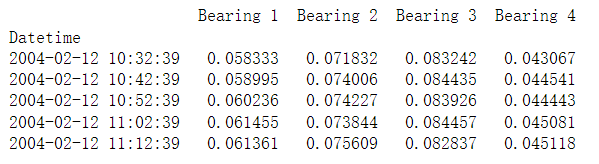
merged_data = pd.read_csv('2nd_test_resmaple_10minutes.csv',index_col='Datetime',usecols=['Datetime','Bearing 1','Bearing 2','Bearing 3','Bearing 4'])
merged_data.index = pd.to_datetime(merged_data.index, format='%Y.%m.%d.%H.%M.%S')
print(merged_data.head())
merged_data.plot()

2. 数据预处理

对于自编码器（深度学习神经网络）来说，至少要进行两个预处理：

• 划分训练集和测试集
• 归一化操作

划分训练集和测试集，可以帮助我们验证自己的模型，并且让模型更加鲁棒。对于异常诊断来说，需要将正常数据放在训练集中。​对于时间序列，我们直接按照时间点进行切分，这里选取2004-02-13 23:52:39。

归一化操作对于神经网络来说至关重要，因为没有归一化，会导致算法无法快速进行梯度下降，在“有生之年”（有限的迭代次数内）无法达到最优解。

# Data pre-processing 
# Split the training and test sets using 2004-02-13 23:52:39 as the cut point
dataset_train = merged_data['2004-02-12 11:02:39':'2004-02-13 23:52:39']
dataset_test  = merged_data['2004-02-13 23:52:39':]
dataset_train.plot(figsize = (12,6))

"""
Normalize data
"""
scaler = preprocessing.MinMaxScaler() # 归一化

X_train = pd.DataFrame(scaler.fit_transform(dataset_train), # Find the mean and standard deviation of X_train and apply them to X_train
                              columns=dataset_train.columns,
                              index=dataset_train.index)

# Random shuffle training data
X_train.sample(frac=1)

X_test = pd.DataFrame(scaler.transform(dataset_test),
                             columns=dataset_test.columns,
                             index=dataset_test.index)

3. 建立自编码模型

创建深度神经网络，较为常用的是Keras （高阶API）以及Tensorflow( 作为Backend），本文即是采用 Tensorflow。

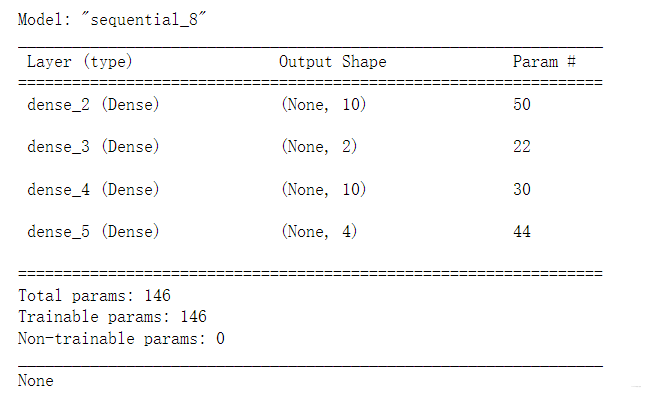
自编码模型一般的神经网络，其内部结构呈现一定对称性。这里我们创建三层神经网络：第一层有10个节点（编码器），中间层有2个节点（编码），第三层有10个节点（解码器）。

一个较好的习惯是，对于神经网络总是从简单模型开始尝试。所以这个三层神经网络会是一个比较好的开始。

激活函数，一般会优先选择“Relu”，当“Relu”无法满足需求的时候，再去考虑其他激活函数，比如Relu的一些衍生版本。这里推荐的激活函数是“Elu”，它是Relu的其中一个优化版本，可以避免出现神经元无法更新的情况。

# Build AutoEncoding model
def AutoEncoder_build(model, X_train, act_func):
    tf.random.set_seed(10)

    # act_func = 'elu'

    # Input layer:
    model = tf.keras.Sequential() # Sequential() is a container that describes the network structure of the neural network, sequentially processing the model

    # First hidden layer, connected to input vector X.
    model.add(tf.keras.layers.Dense(10,activation=act_func, # activation function
                    kernel_initializer='glorot_uniform', # Weight initialization
                    kernel_regularizer=tf.keras.regularizers.l2(0.0), # Regularization to prevent overfitting
                    input_shape=(X_train.shape[1],)
                   )
             )

    model.add(tf.keras.layers.Dense(2,activation=act_func,
                    kernel_initializer='glorot_uniform'))

    model.add(tf.keras.layers.Dense(10,activation=act_func,
                    kernel_initializer='glorot_uniform'))

    model.add(tf.keras.layers.Dense(X_train.shape[1],
                    kernel_initializer='glorot_uniform'))

    model.compile(loss='mse',optimizer='adam') # 设置编译器

    print(model.summary())
    tf.keras.utils.plot_model(model, show_shapes=True)
    
    return model
    
model = tf.keras.Sequential()
model = AutoEncoder_build(model=model,X_train=X_train, act_func='elu')

4. 训练模型

训练模型很简单，只需要调用 fit 函数。需要注意的是，对于自编码器来说，输入和输出都是X_train 特征。 另外我们划分出 5% 的数据集作为验证集来验证模型的泛化性。

def AutoEncoder_main(model,Epochs,BATCH_SIZE,validation_split):
    # Train model for 100 epochs, batch size of 10:
	# noise
    factor = 0.5
    X_train_noise = X_train + factor * np.random.normal(0,1,X_train.shape)
    X_train_noise = np.clip(X_train_noise,0.,1.)
    
    history=model.fit(np.array(X_train_noise),np.array(X_train),
                      batch_size=BATCH_SIZE,
                      epochs=Epochs,
                      shuffle=True,
                      validation_split=validation_split, # Training set ratio
#                       validation_data=(X_train,X_train), # Validation set
                      verbose = 1)

    return history

# Figure
def plot_AE_history(history):
    plt.plot(history.history['loss'],
             'b',
             label='Training loss')
    plt.plot(history.history['val_loss'],
             'r',
             label='Validation loss')
    plt.legend(loc='upper right')
    plt.xlabel('Epochs')
    plt.ylabel('Loss, [mse]')
    plt.ylim([0,.1])
    plt.show()
    
history = AutoEncoder_main(model=model,Epochs=100,BATCH_SIZE=10,validation_split=0.05)

plot_AE_history(history)

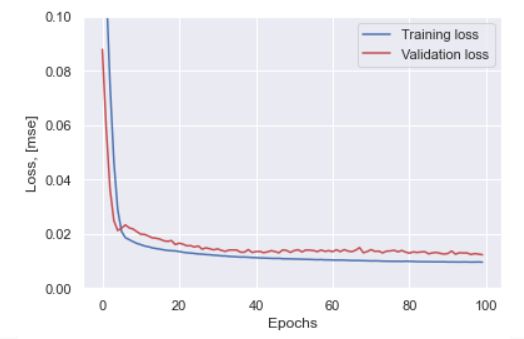当我们查看训练的loss历史曲线时，发现训练集和验证集都很好的进行拟合，而且训练集并没有出现“反弹”，也就是没有过拟合的现象。

5. 查看模型的“认知水平”

当自编码器训练好后，它应该能够学习到原始数据集的内在编码（用很少的维度，比如本案例中为2），然后根据学习到的编码，在一定程度内还原原始数据集。我们可以查看还原的误差分布如何。

X_pred = model.predict(np.array(X_train))
X_pred = pd.DataFrame(X_pred,
                      columns=X_train.columns)
X_pred.index = X_train.index

scored = pd.DataFrame(index=X_train.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_train), axis = 1)
plt.figure()
sns.distplot(scored['Loss_mae'],
             bins = 10,
             kde= True,
            color = 'blue')
plt.xlim([0.0,.5])

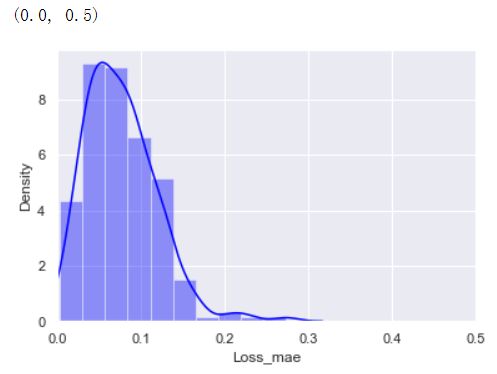
因为该自编码器学习到了“正常数据”的编码格式，所以当一个数据集提供给该自编码器时，它会按照“正常数据”的编码格式去编码和解码。**如果解码后的数据集和输入数据集的误差在一定范围内，则表明输入的数据集是“正常的”，否则是“异常的"。**所以根据上图，我们知道”正常的数据“编码和解码后的误差分布在0.3以内，所以我们可以认为如果一个新的数据集编码，解码之后的误差超出该范围则为异常数据。

6. 对测试集进行异常诊断

基于上面的分析，我们可以确定阈值。接下来我们仅仅需要对测试数据集进行预测，然后将预测的结果误差和阈值进行比对，确认是否为正常数据。

以下代码分别对训练集和测试集进行预测，并且计算解码误差。将误差和阈值对比后，画出趋势图。

X_pred = model.predict(np.array(X_test))
X_pred = pd.DataFrame(X_pred,
                      columns=X_test.columns)
X_pred.index = X_test.index


threshod = 0.3
scored = pd.DataFrame(index=X_test.index)
scored['Loss_mae'] = np.mean(np.abs(X_pred-X_test), axis = 1)
scored['Threshold'] = threshod
scored['Anomaly'] = scored['Loss_mae'] > scored['Threshold']
scored.head()

X_pred_train = model.predict(np.array(X_train))
X_pred_train = pd.DataFrame(X_pred_train,
                      columns=X_train.columns)
X_pred_train.index = X_train.index

scored_train = pd.DataFrame(index=X_train.index)
scored_train['Loss_mae'] = np.mean(np.abs(X_pred_train-X_train), axis = 1)
scored_train['Threshold'] = threshod
scored_train['Anomaly'] = scored_train['Loss_mae'] > scored_train['Threshold']
scored = pd.concat([scored_train, scored])

scored.plot(logy=True,  figsize = (10,6), ylim = [1e-2,1e2], color = ['blue','red'])

可以看到，该方法还是很明显的区分出了正常数据集和异常数据集。对于正常部分来说，可能会有一些”虚假警告“，但是由于其持续时间不长，因此不会给现实的应用造成很大的困扰。因为相比于”提前三天“预警轴承的失效，短短十分钟或者二十分钟的虚假警告，可以通过double check来避免过早行动。

7. 测试

① 获得encoder (功能可以把一张图像压缩为一个向量)

#获得encoder (功能可以把一张图像压缩为一个向量)
encode = tf.keras.Model(inputs=input_dim, outputs=en)
#获得decoder（把一个向量还原回图像)
input_decoder = tf.keras.layers.Input(shape=(hidden_size,))
output__decoder = model.layers[-1](input_decoder)

decode = tf.keras.Model(inputs=input_decoder, outputs=output_decoder)

② 调用encoder把测试集数据压缩为32维向量

#调用encoder把测试集数据压缩为32维向量
#encode_test = encode (x_test) # encode. predict(x_test)可以返回numpy数据(10000, 32)
encode_test = encode. predict(x_test)
encode_test.shape

③ 调用decoder把向量解码回图像

#调用decoder把向量解码回图像
# decode_test = decode (encode_test)
decode_test = decode. predict(encode_test)decode_test.shape
x_test = x_test. numpy ()

8. 完整代码

# Import libraries, core libraries are numpy and sklearn
import os
import pandas as pd
import numpy as np
import tensorflow as tf
from sklearn import preprocessing
import seaborn as sns
sns.set(color_codes=True)
import matplotlib.pyplot as plt

def data_load():
    # Load data set
    folder = r'C:\Users\EliYu\Downloads\archive\2nd_test'
    data_dir = folder+'\\2nd_test'
    merged_data = pd.DataFrame()

    for filename in os.listdir(data_dir):
    #     print(filename)
        dataset = pd.read_csv(os.path.join(data_dir, filename), sep='\t')
        dataset_mean_abs = np.array(dataset.abs().mean())
        dataset_mean_abs = pd.DataFrame(dataset_mean_abs.reshape(1,4))
        dataset_mean_abs.index = [filename]
        merged_data = merged_data.append(dataset_mean_abs)
    merged_data.reset_index(inplace=True)  # reset index to get datetime as columns

    # 将原始数据集聚合为单个csv文件
    merged_data.columns = ['Datetime','Bearing 1','Bearing 2','Bearing 3','Bearing 4'] # rename columns
    merged_data.sort_values(by='Datetime',inplace=True)
    merged_data.to_csv('2nd_test_resmaple_10minutes.csv')

    # 读取数据集
    merged_data = pd.read_csv('2nd_test_resmaple_10minutes.csv',index_col='Datetime',usecols=['Datetime','Bearing 1','Bearing 2','Bearing 3','Bearing 4'])
    merged_data.index = pd.to_datetime(merged_data.index, format='%Y.%m.%d.%H.%M.%S')
    print(merged_data.head())
    merged_data.plot()

    # Data pre-processing
    # Split the training and test sets using 2004-02-13 23:52:39 as the cut point
    dataset_train = merged_data['2004-02-12 11:02:39':'2004-02-13 23:52:39']
    dataset_test  = merged_data['2004-02-13 23:52:39':]
    dataset_train.plot(figsize = (12,6))

    """
    Normalize data
    """
    scaler = preprocessing.MinMaxScaler() # 归一化

    X_train = pd.DataFrame(scaler.fit_transform(dataset_train), # Find the mean and standard deviation of X_train and apply them to X_train
                                  columns=dataset_train.columns,
                                  index=dataset_train.index)

    # Random shuffle training data
    X_train.sample(frac=1)

    X_test = pd.DataFrame(scaler.transform(dataset_test),
                                 columns=dataset_test.columns,
                                 index=dataset_test.index)
    return X_train,X_test


# Build AutoEncoding model
def AutoEncoder_build(model, X_train, act_func):
    tf.random.set_seed(10)

    # act_func = 'elu'

    # Input layer:
    model = tf.keras.Sequential()  # Sequential() is a container that describes the network structure of the neural network, sequentially processing the model

    # First hidden layer, connected to input vector X.
    model.add(tf.keras.layers.Dense(10, activation=act_func,  # activation function
                                    kernel_initializer='glorot_uniform',  # Weight initialization
                                    kernel_regularizer=tf.keras.regularizers.l2(0.0),
                                    # Regularization to prevent overfitting
                                    input_shape=(X_train.shape[1],)
                                    )
              )

    model.add(tf.keras.layers.Dense(2, activation=act_func,
                                    kernel_initializer='glorot_uniform'))

    model.add(tf.keras.layers.Dense(10, activation=act_func,
                                    kernel_initializer='glorot_uniform'))

    model.add(tf.keras.layers.Dense(X_train.shape[1],
                                    kernel_initializer='glorot_uniform'))

    model.compile(loss='mse', optimizer='adam')  # 设置编译器

    print(model.summary())
    tf.keras.utils.plot_model(model, show_shapes=True)

    return model


def AutoEncoder_main(model, Epochs, BATCH_SIZE, validation_split):
    # Train model for 100 epochs, batch size of 10:
    #     Epochs=100
    #     BATCH_SIZE=10

    factor = 0.5
    X_train_noise = X_train + factor * np.random.normal(0,1,size=X_train.shape) # 设置噪声
    history = model.fit(np.array(X_train), np.array(X_train),
                        batch_size=BATCH_SIZE,
                        epochs=Epochs,
                        validation_split=validation_split,  # Training set ratio
                        # shuffle=True,
                        verbose=1)
    return history


def plot_AE_history(history):
    plt.plot(history.history['loss'],
                 'b',
                 label='Training loss')
    plt.plot(history.history['val_loss'],
                 'r',
                 label='Validation loss')
    plt.legend(loc='upper right')
    plt.xlabel('Epochs')
    plt.ylabel('Loss, [mse]')
    plt.ylim([0,.1])
    plt.show()
    

X_train,X_test = data_load()
model = tf.keras.Sequential()
model = AutoEncoder_build(model=model, X_train=X_train, act_func='elu')
history = AutoEncoder_main(model=model,Epochs=100,BATCH_SIZE=10,validation_split=0.05)
plot_AE_history(history)

9. 总结

以上我们完成了第二组数据集代码演示，我们可以用同样的方法（甚至同样的初始化参数）来对其他数据集进行异常检测。

比如第三组数据的结果：我们同样可以提前预测到轴承失效。
本文讲解了如何采用自编码器对异常进行检测，并且在NASA的轴承数据集上进行演示。本文主要讲解代码的实现思路以及一些参数选取的经验分享。最终的模型预测结果可以说是令人满意的，尤其是对于第二组和第三组的测试数据集都能达到很高的预测精度。

三、 附录

1. 关于 os.path.join()

os.path.join()函数用于路径拼接文件路径，可以传入多个路径

① 存在以‘’/’’开始的参数，从最后一个以”/”开头的参数开始拼接，之前的参数全部丢弃。

import os

print(os.path.join('path','abc','yyy'))
# path\abc\yyy

print('1',os.path.join('aaa','/bbb','ccc.txt'))
# 1 /bbb\ccc.txt
 
print('1',os.path.join('/aaa','/bbb','ccc.txt'))
# 1 /bbb\ccc.txt
 
print('1',os.path.join('/aaa','/bbb','/ccc.txt'))
# 1 /ccc.txt
 
print('1',os.path.join('/aaa','bbb','ccc.txt'))
# 1 /aaa\bbb\ccc.txt

② 同时存在以‘’./’与‘’/’’开始的参数，以‘’/’为主，从最后一个以”/”开头的参数开始拼接，之前的参数全部丢弃。

>>> print('2',os.path.join('/aaa','./bbb','ccc.txt'))
2 /aaa\./bbb\ccc.txt
 
print('2',os.path.join('aaa','./bbb','/ccc.txt'))
# 2 /ccc.txt

③ 只存在以‘’./’开始的参数,会从”./”开头的参数的上一个参数开始拼接。

print('2',os.path.join('aaa','./bbb','ccc.txt'))
# 2 aaa\./bbb\ccc.txt

④ 注意：

path='C:/yyy/yyy_data/'
print(os.path.join(path,'/abc'))
# C:/abc

print(os.path.join(path,'abc'))
# C:/yyy/yyy_data/abc

2. 关于 sns.set (Seaborn 绘图风格设置)

sns.set()设置风格
seaborn.set()函数参数：

seaborn.set(context=‘notebook’, style=‘darkgrid’, palette=‘deep’, font=‘sans-serif’, font_scale=1, color_codes=True, rc=None)

Seaborn其实是在matplotlib的基础上进行了更高级的API封装，从而使得作图更加容易，在大多数情况下使用seaborn就能做出很具有吸引力的图，为数据分析提供了很大的便利性。但是应该把Seaborn视为matplotlib的补充，而不是替代物。

从这个set()函数，可以看出，通过它我们可以设置背景色、风格、字型、字体等。我们定义一个函数，这个函数主要是生成100个0到15的变量，然后用这个变量画出6条曲线。

def sinplot(flip=2):
    x = np.linspace(0, 15, 100)
    for i in range(1, 6):
        plt.plot(x, np.sin(x + i * .5) * (7 - i) * flip)
sns.set()
sinplot()

3. 关于 preprocessing.MinMaxScaler

preprocessing.MinMaxScaler 是归一化操作的函数，当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到 [0,1] 之间，而这个过程，就叫做数据归一化(Normalization，又称Min-Max Scaling)。注意，Normalization是归一化，不是正则化，真正的正则化是regularization，不是数据预处理的一种手段。归一化之后的数据服从正态分布，公式如下：
$$x^{\ast }=\frac{x-\min (x)}{\max (x)-\min (x)}$$
​​
在sklearn当中， 使用 preprocessing.MinMaxScaler 来实现这个功能。MinMaxScaler有一个重要参数，feature_range，控制我们希望把数据压缩到的范围，默认是[0,1] .

class sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1),copy=True)

4. StandardScaler类中transform和fit_transform方法有什么区别？

StandardScaler类是一个用来讲数据进行归一化和标准化的类。
所谓归一化和标准化，即应用下列公式：
$$X=(x-\mu )/\sigma$$
答：fit_transform方法是fit和transform的结合，fit_transform(X_train) 意思是找出X_train的均值和​​​​​​​标准差，并应用在X_train上。
这时对于X_test，我们就可以直接使用transform方法。因为此时StandardScaler已经保存了X_train的均值和标准差

1. 二者的功能都是对数据进行某种统一处理（比如标准化~N(0,1)，将数据缩放(映射)到某个固定区间，归一化，正则化等）。
2. fit_transform(partData)对部分数据先拟合fit，找到该part的整体指标，如均值、方差、最大值最小值等等（根据具体转换的目的），然后对该partData进行转换transform，从而实现数据的标准化、归一化等等。
3. 根据对之前部分fit的整体指标，对剩余的数据（restData）使用同样的均值、方差、最大最小值等指标进行转换transform(restData)，从而保证part、rest处理方式相同。
4. 必须先用fit_transform(partData)，之后再transform(restData)，如果直接transform(partData)，程序会报错。
5. 如果fit_transfrom(partData)后，使用fit_transform(restData)而不用transform(restData)，虽然也能归一化，但是两个结果不是在同一个“标准”下的，具有明显差异。

5. Keras kernel_initializer 权重初始化的方法

Keras kernel_initializer 权重初始化，不同的层可能使用不同的关键字来传递初始化方法，一般来说指定初始化方法的关键字是kernel_initializer 和 bias_initializer，例如：

model.add(Dense(64,
                kernel_initializer='random_uniform',
                bias_initializer='zeros'))

6. Keras的正则化Regularizers

正则化器的概念
正则化器允许在优化过程中对层的参数或层的激活情况进行惩罚。 网络优化的损失函数也包括这些惩罚项。

tensorflow2.0内置正则项
  在隐藏层中经常会使用正则来作为损失函数的惩罚项。换言之，为了约束w的可能取值空间从而防止过拟合，我们为该最优化问题加上一个约束，就是w的L1范数或者L2范数不能大于给定值。
  L2正则被用于防止模型的过拟合，L1正则项被用于产生稀疏权值矩阵。
  tf.keras.regularizers提供了几种内置类来提供正则。分别是class L1、class L1L2、class L2、class Regularizer 、serialize。同时提供了三个参数作为可被正则化的对象：

• kernel_regularizer : 对该层中的权值矩阵layer.weights正则
• bias_regularizer : 对该层中的偏差矩阵layer.bias正则
• activity_regularizer : 对该层的输出值矩阵layer.bias正则

调用kernel_regularizer=tf.keras.regularizers.l1_l2(l1=0.02, l2=0.01)时，$losses=L_1+L_2=l_1\sum (|w_{ij}|)+l_2\sum (w_{ij}^2)$

import tensorflow.keras as keras
keras.regularizers.l1(0.)  # L1范式正则
keras.regularizers.l2(0.)  # L2范式正则
keras.regularizers.l1_l2(l1=0.01, l2=0.01)  # L1范式，L2范式同时正则

#定义新的正则化器
#任何输入一个权重矩阵、返回一个损失贡献张量的函数，都可以用作正则化器，例如：

import tensorflow.keras as keras
def l1_reg(weight_matrix):
    return 0.01 * K.sum(K.abs(weight_matrix))

model.add(Dense(64, input_dim=64,
                kernel_regularizer=l1_reg))

7. 关于 model.fit()

model.fit( x, y, batch_size=32, epochs=10, verbose=1, callbacks=None,
validation_split=0.0, validation_data=None, shuffle=True, 
class_weight=None, sample_weight=None, initial_epoch=0)

• x：输入数据。如果模型只有一个输入，那么x的类型是numpy
  array，如果模型有多个输入，那么x的类型应当为list，list的元素是对应于各个输入的numpy array

• y：标签，numpy array

• batch_size：整数，指定进行梯度下降时每个batch包含的样本数。训练时一个batch的样本会被计算一次梯度下降，使目标函数优化一步。

• epochs：整数，训练终止时的epoch值，训练将在达到该epoch值时停止，当没有设置initial_epoch时，它就是训练的总轮数，否则训练的总轮数为epochs - inital_epoch

• verbose：日志显示，0为不在标准输出流输出日志信息，1为输出进度条记录，2为每个epoch输出一行记录

• callbacks：list，其中的元素是keras.callbacks.Callback的对象。这个list中的回调函数将会在训练过程中的适当时机被调用，参考回调函数

• validation_split：0~1之间的浮点数，用来指定训练集的一定比例数据作为验证集。验证集将不参与训练，并在每个epoch结束后测试的模型的指标，如损失函数、精确度等。注意，validation_split的划分在shuffle之前，因此如果你的数据本身是有序的，需要先手工打乱再指定validation_split，否则可能会出现验证集样本不均匀。

• validation_data：形式为（X，y）的tuple，是指定的验证集。此参数将覆盖validation_spilt。

• shuffle：布尔值或字符串，一般为布尔值，表示是否在训练过程中随机打乱输入样本的顺序。若为字符串“batch”，则是用来处理HDF5数据的特殊情况，它将在batch内部将数据打乱。

• class_weight：字典，将不同的类别映射为不同的权值，该参数用来在训练过程中调整损失函数（只能用于训练）

• sample_weight：权值的numpy.array，用于在训练时调整损失函数（仅用于训练）。可以传递一个1D的与样本等长的向量用于对样本进行1对1的加权，或者在面对时序数据时，传递一个的形式为（samples，sequence_length）的矩阵来为每个时间步上的样本赋不同的权。这种情况下请确定在编译模型时添加了sample_weight_mode=’temporal’。

• initial_epoch: 从该参数指定的epoch开始训练，在继续之前的训练时有用。

• fit函数返回一个History的对象，其History.history属性记录了损失函数和其他指标的数值随epoch变化的情况，如果有验证集的话，也包含了验证集的这些指标变化情况

8. 关于 KL散度(KL Divergence)

$$KL(P||Q)={\int }_{-\infty }^{\infty }p(x)log\frac{p(x)}{q(x)}dx$$
Python scipy.stats.entropy用法及代码示例

scipy.stats.entropy(pk, qk=None, base=None, axis=0)
# 计算给定概率值的分布熵。

如果仅给出概率 pk，则熵计算为 S = -sum(pk * log(pk), axis=axis) 。

如果 qk 不是 None，则计算 Kullback-Leibler 散度 $S=KL(P||Q)={\int }_{-\infty }^{\infty }p(x)log\frac{p(x)}{q(x)}dx$

如果 pk 和 qk 的总和不为 1，则此例程将标准化。

参数：

• pk： array_like 定义(离散)分布。沿着 pk 的每个 axis-slice ，元素 i 是事件 i 的(可能未归一化的)概率。

• qk： 数组，可选 计算相对熵的序列。应该与pk的格式相同。

• base： 浮点数，可选 要使用的对数底数，默认为e(自然对数)。

• axis： 整数，可选 计算熵的轴。默认值为 0。

返回：

• S： {浮点数，数组} 计算的熵。

不同 p 的伯努利试验。公平硬币的结果是最不确定的：

from scipy.stats import entropy
entropy([1/2, 1/2], base=2)
#1.0
有偏见的硬币的结果不太不确定：

entropy([9/10, 1/10], base=2)
#0.46899559358928117
相对熵：

entropy([1/2, 1/2], qk=[9/10, 1/10])
#0.5108256237659907