机器学习-SVM支持向量机模型详解

SVM设计初衷

解决二分类问题

有关概念

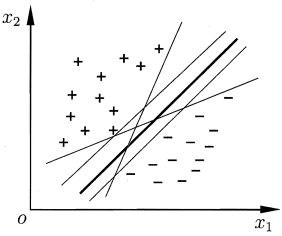
线性可分：上图中+与-分别代表两类数据，而这图中的直线可以分隔这两类数据，这种能够通过一条直线将两类数据分隔开的分类情况，我们称其线性可分。
分隔超平面：上述将数据集分隔开来的直线称为分隔超平面。
超平面：上述图像由于数据点都在二维平面上，所以分隔超平面就只是一条直线，而当数据点在n维上时，就需要n-1维的某某对象来对数据进行分隔，该对象被称为超平面，也就是分类的决策边界。
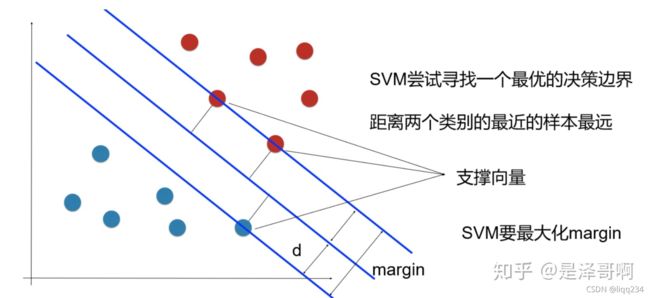
间隔：上图中我们发现有多条直线可以将数据分成两类，而我们希望的是遇到不在训练集中的点时，某条直线能够很好的正确分类，此时我们需要找到离分隔超平面最近的点，确保她们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔（点相对于分隔面的间隔）；而数据集中所有点到分隔面的最小间隔的2倍，称为分类器或者数据集的间隔。
支持向量：上述离分隔超平面最近的那些点就被称为支持向量。

划分超平面用线性方程表示：
$$w^{T}x+b=0$$
样本空间中任意点x到超平面(w,b)的距离可写为
$$r=\frac{|w^{T}x+b|}{||w||}$$

SVM分类

• hard-margin SVM 又称最大间隔分类器
• soft-margin SVM
• kernel SVM

hard-margin SVM算法

目的

解决max margin$(w,b)$ $$s.t\{\begin{array}{ll}{w}^T{x}_i+b,& \text{yi=+1}\\ w^T{x}_i+b,& \text{yi=−1}\end{array}$$
的问题。

公式

其中
$$margin(w,b)=mindistance(w,b,x_i)=min\frac{|w^{T}x+b|}{||w||},i=1,2...,N$$
从而得到$$maxmargin(w,b)=\{\begin{array}{l}maxmin\frac{|w^{T}x+b|}{||w||}=max\frac{1}{||w||}min|w^T{x}_i+b|,w,b,x_i,i=1...N\\ s.t{y}_i(w^{T}x+b)>0⟹\exists r>0,s.t.min{y}_i(w^T{x}_i+b)=r\end{array}$$
其中r可以直接归一化为1
从而得到
$$maxmargin(w,b)=max\frac{1}{||w||}s.t{y}_i(w^T{x}_i+b)\ge 1⟹min\frac{1}{2}{w}^{T}ws.t.y_i(w^T{x}_i+b)\ge 1,for\forall i=1,...N$$
其中$y_i(w^{T}x+b)\ge 1$可写成$1-y_i(w^{T}x+b)\le 0$。
这便是一个凸优化问题，共有N个约束。

对偶问题引出

目的

利用拉格朗日乘数法求解上述受多个条件约束的多元函数极值的问题

公式推导关键步骤

$$f(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^n{\lambda }_i(1-y_i(w^{T}x+b));\lambda \ge 0,1-y_i(w^{T}x+b)\le 0$$
即求$$\{\begin{array}{l}\underset{w,b}{\min }\underset{\lambda }{\max }f(w,b.\lambda )\\ s.t.{\lambda }_i\ge 0\end{array}$$
上述两个公式为原问题，将其转换为对偶问题
$$\{\begin{array}{l}\underset{\lambda }{\max }\underset{w,b}{\min }f(w,b,\lambda )(1)\\ s.t.{\lambda }_i\ge 0\end{array}$$
对偶问题与原问题同解。

求解对偶问题

先求$$\underset{w,b}{\min }f(w,b,\lambda )$$
对$b$求偏导
$$\begin{array}{rl}\frac{\partial f}{\partial b}=& \frac{\partial }{\partial b}[\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i(w^T{x}_i+b)]\\ =& \frac{\partial }{\partial b}[-\sum _{i=1}^N{\lambda }_i{y}_{i}b]\\ =& -\sum _{i=1}^N{\lambda }_i{y}_i=0⟹\sum _{i=1}^N{\lambda }_i{y}_i\stackrel{\Delta }{=}0\end{array}$$
将其代入$f(w,b,\lambda )$
$$\begin{array}{rl}f(w,b,\lambda )=& \frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i(w^T{x}_i+b)\\ =& \frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i-\sum _{i=1}^N{\lambda }_i{y}_{i}b\\ =& \frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i\end{array}$$
对$w$求偏导(涉及矩阵求导法则)
$$\begin{array}{rl}\frac{\partial f}{\partial w}=& \frac{1}{2}2w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i\stackrel{\Delta }{=}0⟹w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i\end{array}$$
将其代入$f(w,b,\lambda )$
$$\begin{array}{rl}f(w,b,\lambda )=& \frac{1}{2}(\sum _{i=1}^N{\lambda }_i{y}_i{x}_i{)}^T(\sum _{i=1}^N{\lambda }_j{y}_j{x}_j)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i(\sum _{i=1}^N{\lambda }_j{y}_j{x}_j{)}^T{x}_i\\ =& -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\lambda }_i\end{array}$$
则$(1)$式对偶问题演变成
$$\{\begin{array}{l}\underset{\lambda }{\max }-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+{\sum }_{i=1}^N{\lambda }_i\\ s.t.{\lambda }_i\ge 0\\ {\sum }_{i=1}^N{\lambda }_i{y}_i=0\end{array}$$
原问题，对偶问题具有强对偶关系$⟺$满足KKT条件。

KKT条件

$$\{\begin{array}{l}\frac{\partial f}{\partial w}=0;\frac{\partial f}{\partial b}=0;\frac{\partial f}{\partial \lambda }=0\\ {\lambda }_i(1-y_i(w^{T}x+b))=0\\ {\lambda }_i\ge 01-y_i(w^T{x}_i+b)\le 0\end{array}$$
可得
$$w^{\ast }=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i;b^{\ast }=y_k-\sum _{i=0}^N{\lambda }_i{y}_i{x}_i^T{x}_k$$
即决策函数为
$$h(x)=sign((w^{\ast }{)}^{T}x+b\ast )$$

soft-margin SVM算法

思想

允许有一点点错误，即求$$min\frac{1}{2}{w}^{T}w$$可以演变为求$$min\frac{1}{2}{w}^{T}w+loss$$
$$loss=max(0,1-y_i(w^T{x}_i+b))(hinge-loss)$$
即soft-margin解决的是
$$\{\begin{array}{l}min\frac{1}{2}{w}^{T}w+C{\sum }_{i=1}^{N}max\{0,1-y_i(w^T{x}_i+b)\}\\ s.t.y_i(w^{T}x+b)\ge 1\end{array}$$
引入一个变量${\xi }_i=1-y_i(w^T{x}_i+b),{\xi }_i\ge 0$将上式变为
$$\{\begin{array}{l}min\frac{1}{2}{w}^{T}w+C{\sum }_{i=1}^N{\xi }_i\\ s.t.y_i(w^{T}x+b)\ge 1-{\xi }_i,{\xi }_i\ge 0\end{array}$$
其求解与hard-margin SVM基本一致，可自行推导。

应用场景

SVM是最接近深度学习的机器学习算法。

1. 手写识别数字
2. 人脸识别
3. 图像分类
4. 蛋白质分类

代码实现示例

优缺点

待更新。。。