基于SVM的点云分类--python实现

写在前面的话

主要使用了PCA相关特征和平面拟合残差对点云进行分类。
主要是对该博主文章的复现（在此致谢，如有侵权请联系我），使得整体代码更加紧凑，方便阅读和理解。
点云特征计算主要借助于open3d，点云分类主要借助于sklearn。
得益于sklearn的优秀的接口设计，sklearn机器学习分类步骤大同小异。其主要步骤：
0预处理：将所有点云去掉地面点，只保留非地面点
1选择样本点云
2选择特征，并计算样本点云特征
3选择机器学习方法训练模型
4计算待分类点云的特征
5将特征代入模型预测分类结果。

样本

我这里分别对建筑物和植被进行分类。

实现

show the codes:

import open3d as o3d
import numpy as np
from sklearn import svm
from sklearn.neighbors import NearestNeighbors

'''
使用3个特征进行点云分类：发散系数和线状特征,平面拟合残差(粗糙度)
'''


#计算最小二乘平面及距离(粗糙度)
def CaculateAverageSquareDistance(p):
    num = p.shape[0]
    B = np.zeros((p.shape[0],3))
    one = np.ones((p.shape[0],1))
    B[:,0] = p[:,0]
    B[:,1] = p[:,1]
    B[:,2] = one[:,0]
    l = p[:,2]
    BTB = np.matmul(B.T,B)
    BTB_1 = np.linalg.pinv(BTB)
    temp = np.matmul(BTB_1,B.T)
    result = np.matmul(temp,l)
    V  = np.matmul(B,result)-l
    sum = 0
    for i in range (0,V.shape[0]):
        sum = sum+V[i]**2
    return sum/V.shape[0]


# 计算发散系数、线状特征
def computePointPCA(pointcloud):

    # 计算整块点云的均值和协方差
    mean_convariance = pointcloud.compute_mean_and_covariance()
    # 特征分解得到特征值
    eigen_values, eigen_vectors = np.linalg.eig(mean_convariance[1])
    sorted_indices = np.argsort(eigen_values)
    # min_indice=sorted_indices[0,0]
    # 发散系数=最小特征值除以最大特征值
    scattering = eigen_values[sorted_indices[0]] / eigen_values[sorted_indices[2]]
    # 线状特征=（最大特征值-次大特征值）/最大特征值
    line_feature=(eigen_values[sorted_indices[2]]-eigen_values[sorted_indices[1]])/eigen_values[sorted_indices[2]]
    point_feature=[]
    point_feature.append(scattering)
    point_feature.append(line_feature)
    return point_feature


# 计算点云中的每个点的发散系数、线状特征
def computeCloudFeature(pcd):
    pcd_tree = o3d.geometry.KDTreeFlann(pcd)
    k = 50
    point_feature_list = []
    for point in pcd.points:
        [n, idx, _] = pcd_tree.search_knn_vector_3d(point, k)
        #[n, idx, _] = pcd_tree.search_radius_vector_3d(point, 0.2)
        # 转为np 获取近邻点
        neigh_points_array = np.array(pcd.points)[idx[1:], :]
        # 重新转为pointcloud
        neigh_pointcloud = o3d.geometry.PointCloud()
        neigh_pointcloud.points = o3d.utility.Vector3dVector(neigh_points_array)
        shape = neigh_points_array.shape
        # 点云数量不能小于3
        if shape[0] > 5:
            # 计算发散系数、线状特征
            point_feature = computePointPCA(neigh_pointcloud)
            #粗糙度
            point_roughness=CaculateAverageSquareDistance(neigh_points_array);
            point_feature.append(point_roughness)
            point_feature_list.append(point_feature)
    return point_feature_list


def writeData(path, features, type):
    f = open(path, 'w')
    for feature in features:
        f.writelines(str(feature) + "," + str(type) + "\n")
    f.close()


def writeData2(path, features, type):
    f = open(path, 'a')
    for feature in features:
        f.writelines(str(feature) + "," + str(type) + "\n")
    f.close()


# 按间距中的绿色按钮以运行脚本。
if __name__ == '__main__':
    # 计算训练数据特征
    # 建筑物特征
    building_train_path = "./building_train2.pcd"
    pcd = o3d.io.read_point_cloud(building_train_path)
   # o3d.visualization.draw_geometries([pcd])
    # scatter = computePointPCA(pcd)
    building_list_feature = computeCloudFeature(pcd)

    # 分别保存
    #writeData("./building2_feature.txt", building_list_scatter, 1)
    # 树木特征
    tree_train_path = "./tree_train2.pcd"
    tree_pcd = o3d.io.read_point_cloud(tree_train_path)
    tree_list_feature = computeCloudFeature(tree_pcd)
    # 分别保存
   # writeData("./tree2_feature.txt", tree_list_scatter, 2)
    # 保存到一个文件
    # writeData2("./feature.txt", building_list_scatter, 1)
    # writeData2("./feature.txt", tree_list_scatter, 2)

    # 转成np
    # building
    building_feature_array = np.array(building_list_feature)

    # 建筑物y=1
    y_building = np.full((building_feature_array.shape[0], 1), 1)
    # tree
    tree_feature_array = np.array(tree_list_feature)

    y_tree = np.full((tree_feature_array.shape[0], 1), 2)
    # 得到训练数据集
    train_x = np.concatenate((building_feature_array, tree_feature_array), axis=0)
    train_y = np.concatenate((y_building, y_tree), axis=0)
    # 读取待分类的点云
    predict_points = o3d.io.read_point_cloud("./predict_data3.pcd")
    predict_points_feature = computeCloudFeature(predict_points)
    # 训练
    clf = svm.SVC()
    # x_train2 = np.array(train_x).reshape(-1, 1)
    clf.fit(train_x, train_y)
    # 分类并保存
    f = open("./分类点云3特征.txt", "w")
    points = np.asarray(predict_points.points)

    for i in range(np.array(predict_points_feature).shape[0]):
        # 预测
        x=points[i,0]
        y=points[i,1]
        z=points[i,2]
        ff=np.array(predict_points_feature[i])
        #必须reshape
        label = clf.predict(np.array(predict_points_feature[i]).reshape(1,3))
        f.write(str(x) + " " + str(y) + " " + str(z) + " " + str(label[0]) + "\n")
    # 保存点云与分类结果
    f.close()

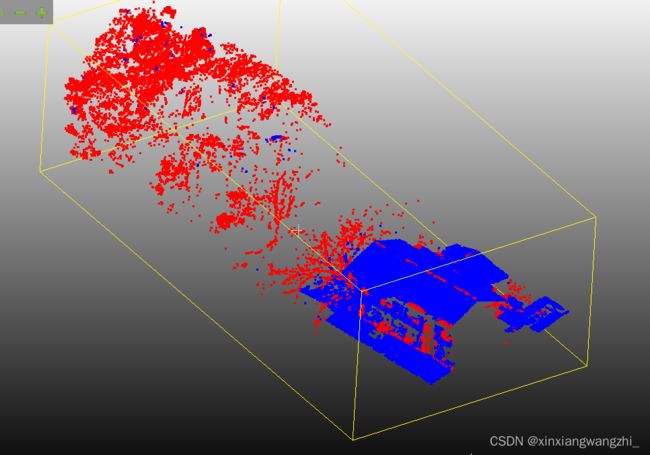
分类结果

结果意料之中，对屋顶边缘容易出现误分类。分类的效果往往取决于特征的选择。另外特征计算用到PCA和特征分解，这两个都很耗时。如果应用到工程中还有许多要改进的地方。