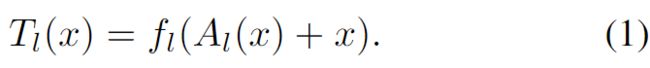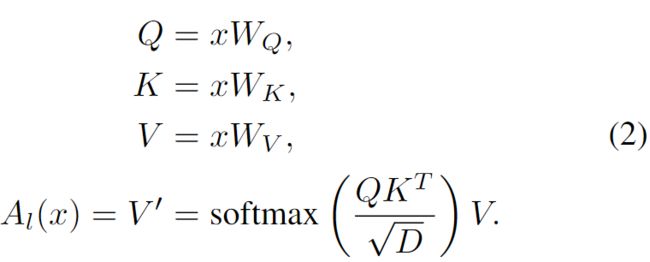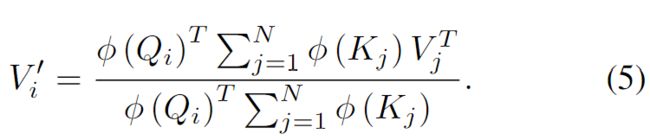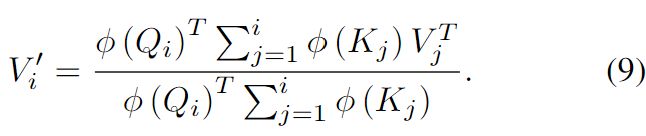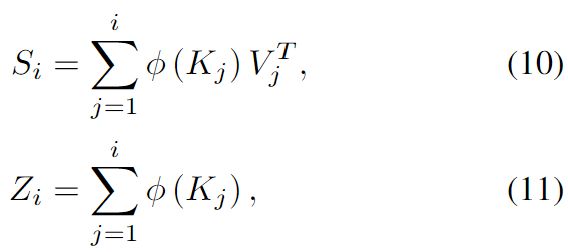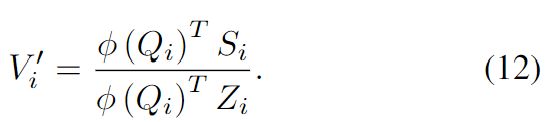【Transformer架构】Transformers are RNNs （linear transformer）

原始题目：Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention

中文翻译：Transformers 是RNNs: 带线性Attention的快速自回归Transformers

发表时间：2020 年 6 月 29 日

平台：ICML 2020

来源：Idiap Research Institute, Switzerland

文章链接：https://arxiv.org/pdf/2006.16236v3.pdf

开源代码：GitHub - idiap/fast-transformers: Pytorch library for fast transformer implementations

摘要

        Transformers 在一些任务中取得了显著的性能，但由于其二次复杂度(相对于输入长度)，对于非常长的序列，它们的速度会非常慢。为了解决这一限制，我们将 self-attention 表示为核特征图的线性点积，并利用矩阵乘积的结合性将复杂度从降低到O (N)，其中N为序列长度。我们展示了这种公式允许迭代实现，极大地加速了自回归Transformers ，并揭示了它们与循环神经网络的关系。我们的线性Transformers 实现了与普通Transformers 相似的性能，并且在非常长的序列的自回归预测方面快了4000倍。

5. 结论

        在这项工作中，我们提出了一种线性Transformer模型，它可以显著降低原始Transformer 的内存和计算成本。特别地，通过利用矩阵乘积的结合性，我们能够计算出时间和内存上的 self-attention，它们与序列长度成线性比例。我们表明，我们的模型可以使用因果掩蔽（ masking），并仍然保留其线性渐近复杂度。最后，我们将Transformer 模型表示为一个循环神经网络，这使我们能够更快地对自回归任务进行推理。

        这一特性为未来在 RNNs和 Transformers 中存储和检索信息的研究开辟了许多方向。另一个有待探索的研究方向是线性 attention 特征图的选择。例如，用随机傅里叶特征逼近RBF核可以允许我们使用 用softmax attention预训练的模型。

1. 引言

        Transformers 模型最初是由Vaswani等人(2017)在神经机器翻译的背景下引入的(Sutskever等人，2014;Bahdanau等人，2015年)，并在处理自然语言(Devlin等人，2019年)、音频(Sperber等人，2018年)和图像(Parmar等人，2019年)的各种任务上展示了令人印象深刻的结果。除了有充分监督的任务外，当用自回归(Radford et al., 2018; 2019) 或掩码语言建模目标 (Devlin et al., 2019; Yang et al., 2019; Song et al., 2019; Liu et al., 2020)进行预训练时，Transformers 也能有效地将知识转移任务中，这些任务是有限制的或无监督的。

        然而，这些好处往往伴随着非常高的计算和内存成本。这种瓶颈主要是由于self-attention的全局感受野以二次空间和时间复杂度处理N个输入的上下文，导致Transformers 在实际应用中训练缓慢，其上下文是受限制的。这破坏了时间连贯性，并阻碍了长期依赖的捕获。Dai等人(2019)通过关注来自以前上下文的记忆来解决后者，尽管以牺牲计算效率为代价。

 后者这里指的是 破坏时间的连贯性

        最近，研究人员关注在不牺牲效率的前提下增加上下文长度的方法上。为此，Child等人(2019)引入了  attention 矩阵的稀疏分解，将 self-attention复杂度降低到。Kitaev等人(2020)使用位置敏感哈希( locality sensitive hashing)进一步将复杂性降低到O (N logN)。这使得长序列的缩放(scaling)成为可能。尽管上述模型可以有效地训练大序列，但它们不能加速自回归推理。

        在本文中，我们引入了线性 transformer 模型，显著减少内存占用，并与上下文长度线性缩放。我们通过使用基于核的 self-attention 公式和矩阵乘积的关联属性来计算self-attention权重(3.2节)来实现这一点。使用我们的线性公式，我们也用线性复杂性和常数内存来表示因果掩蔽(3.3)。这揭示了transformers和 RNNs之间的关系，这使我们能够更快地执行自回归推断，速度快几个数量级(3.4)。

        我们对图像生成和自动语音识别的评估表明， linear transformer 可以达到 transformer 的性能水平，同时在推理过程中速度提高3个数量级。

2. 相关工作

        在本节中，我们提供了寻求解决 transformers 大内存和计算需求的最相关的工作的概述。此外，还讨论了对 transformers 模型的核心部件—— self-attention 进行理论分析的方法。最后，我们提出了另一项工作，旨在缓解 attention 计算中的softmax瓶颈。

2.1. 高效Transformers

        现有的研究试图通过权重剪枝（weight pruning） (Michel等人，2019年)、权重因数分解（weight factorization）(Lan等人，2020年)、权重量化(Zafrir等人，2019年)或知识蒸馏来提高transformers 的内存效率。Clark等人(2020)提出了一种新的预训练目标，称为替换 token 检测，它的采样效率（sample efficient）更高，减少了整体计算。Lample等人(2019)使用 product-key attention 来增加任何层的容量，而计算开销忽略不计。

        使用这些方法减少内存或计算需求，导致训练或推断时间加速，但从根本上说，时间复杂度仍然是二次的序列长度，这阻碍了扩展（ scaling）到长序列。相反，我们表明，我们的方法在理论上(3.2)和经验上(4.1)都降低了transformers 的空间和时间复杂度。

        另一项研究旨在增加transformers 中 self-attention 的“上下文”（ "context"）。上下文指的是序列中用于计算 self-attention 的最大部分。Dai等人(2019)推出了Transformer-XL，通过学习固定长度上下文以外的依赖性，而不破坏时间连续性，实现了最先进的语言建模。但是，在内存中维护以前的上下文会带来大量额外的计算成本。与此相反，Sukhbaatar等人(2019)通过学习每个 attention head 的最优attention 跨度（attention span），显著延长了上下文长度，同时保持对内存占用和计算时间的控制。注意，两种方法都具有与普通模型相同的渐近复杂度。相比之下，我们改善了 self-attention的渐近复杂度，这让我们可以使用更大的 context。

        与我们的模型更相关的是Child等人(2019)和Kitaev等人(2020)的作品。前者(Child et al.， 2019)引入了 attention 矩阵的稀疏分解（ sparse factorizations），降低了二次复杂度到的整体复杂度，用于长序列的生成式建模。最近，Kitaev等人(2020)提出了Reformer。该方法通过使用位置敏感哈希( locality-sensitive hashing (LSH))来减少点积，进一步将复杂度降低到O (N logN)。注意，为了能够使用LSH,  对于 attention，Reformer将 keys 约束为与queries 相同。因此，此方法不能用于解码  keys需要与 queries 不同的任务。相比之下， linear transformers 对 queries 和 keys 没有限制，并且与序列长度线性比例（ scale）。此外，它们可以用于在自回归任务中执行推理，速度快三个数量级，在验证复杂度方面达到相当的性能。

2.2. 理解 Self-Attention

        从理论角度更好地理解 self-attention的努力很少。蔡等人（2019）提出了一种基于内核的transformers  attention公式，将 attention 视为在输入上应用内核平滑器（ kernel smoother），内核分数是输入之间的相似性。这个公式提供了一种更好的方式来理解注意力组件和整合位置嵌入。相比之下，我们使用内核公式来加快 self-attention 的计算并降低其计算复杂度。此外，我们观察到，如果将具有正相似性分数的内核应用于queries和 keys，则线性 attention 通常会收敛。
        最近，Cordonnier 等人（2020）提供了理论证明和经验证据，证明具有足够数量的head的 multi-head selfattention 可以表达任何卷积层。在这里，我们改为展示使用自回归目标训练的 self-attention层 可以看作是循环神经网络，并且这种观察可以用来显著加快自回归 transformer 模型的推理时间。

2.3. 线性化softmax

        多年来，softmax 一直是训练具有大量类别的分类模型的瓶颈（Goodman, 2001; Morin & Bengio, 2005; Mnih & Hinton, 2009）。 最近的工作 (Blanc & Rendle, 2017; Rawat et al., 2019) 使用特征图的线性点积来逼近 softmax，以通过采样加速训练。 受这些工作的启发，我们将 transformers 中的 softmax  attention 线性化。 在这项工作的同时，Shen 等人（2020 年）探索了将线性 attention 用于图像中目标检测的任务。 相比之下，我们不仅将 attention 计算线性化，而且还开发了一个具有线性复杂度和常数内存的自回归变换器模型，用于推理和训练。 此外，我们表明，通过内核的镜头，每个 transformer 都可以看作是一个循环神经网络。

3.  Linear Transformers

        在本节中，我们将我们提出的 linear transformer 公式化。 我们提出，将注意力从传统的 softmax 注意力转移到基于特征图的点积注意力会导致更好的时间和空间复杂度以及可以在线性时间内执行序列生成的因果模型，类似于递归神经网络。
        最初，在第 3.1 节中，我们介绍了 (Vaswani et al., 2017) 中介绍的 Transformer 架构的公式。 随后，在第 3.2 节和第 3.3 节中，我们提出了 linear transformer，最后，在第 3.4 节中，我们将 transformer重写为循环神经网络。

3.1. Transformers

        ，序列长度=N，特征维度 = F。一个 Transformer 是一个函数  ，通过 L 个 transformer 层 (·), . . . , (·) 的组成定义，如下：

        函数 (·) 独立于其他特征变换每个特征，通常用一个小型的两层前馈网络实现。 (·) 是 self -attention函数，是  transformer 中唯一跨序列起作用的部分。

只有 self -attention 涉及到了跨序列变换。

         self-attention 函数 (·) 为每个位置计算所有其他位置的特征表示的加权平均值，其权重与表示之间的相似性分数成正比。 形式上，输入序列 由三个矩阵 、 和 投影到相应的表示 Q、K 和 V。 所有位置的输出，(x) = V '，计算如下：

 Q: NxD; K^T: DxN -> NxN  x   V: NxM  -> NxM

        请注意，在前面的等式中，softmax 函数 行级别(rowwise) 应用于 。 按照通用术语，Q、K 和 V 分别称为 "queries"、 "keys" 和"values"。

        方程2实现了一种特殊形式的 self-attention，称为 softmax attention，其中相似度分数是一个 query 和一个 key 之间点积的指数。假设矩阵下标为，将返回矩阵的第行作为一个向量，我们可以对任意相似函数写出如下广义 attention 方程:

         如果将相似函数代入，则方程3与方程2等价。

 3.2. Linearized Attention 线性化的Attention 

        方程2中 attention 的定义是通用的，可以用来定义其他几种 attention 实现，如多项式（polynomial）attention或 RBF kernel attention (Tsai et al.， 2019)。请注意，为了让方程3定义一个 attention 函数，我们需要对sim(·) 施加的唯一约束是非负的。这包括所有的kernels 。

        给这样一个特征表示 的一个核，我们可以定义公式2 如下：

         然后利用矩阵乘法的结合律进一步简化为：

         当分子以向量形式表示时，上面的方程更简单：

         注意，特征映射被行应用于矩阵Q和K。

        由式2可知，softmax  attention 尺度的计算代价为，其中N表示序列长度。对于内存需求也是如此，因为必须存储完整的 attention 矩阵来计算关于 queries、 keys 和 values 的梯度。相比之下，由公式5提出的 linear transformer 的时间和内存复杂度为O(N)，因为我们可以一次计算和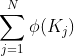，并在每次 query 时重新使用它们。

3.2.1 特征图和计算成本

        对于softmax attention，乘法和加法的总成本规模为，其中是 queries和 keys的维度是D，values 的维度是M。相反，对于 linear attention，我们首先计算C维的特征图。随后，计算新的 values 需要O(NCM )加法和乘法。

        前面的分析没有考虑到 kernel 和 feature function 的选择。请注意，对应于指数核的特征函数是无限维的，这使得精确softmax attention的线性化不可行。另一方面，多项式核，例如，具有精确的有限维特征图已被证明与指数核或RBF核同样工作良好(Tsai等人，2019)。线性化2次多项式 transformer 的计算代价为。当 时，这使得计算复杂度有利。注意，这在实践中是正确的，因为我们希望能够处理具有数万个元素的序列。

        对于我们处理较小序列的实验，我们使用了一个特征映射，其结果为正相似函数，定义如下：

        其中 elu(·) 表示指数线性单元(Clevert et al.， 2015)激活函数。我们更喜欢 elu(·) 而不是relu(·)，以避免在 x 为负时将梯度设置为0。这个特征映射产生了一个需要O (NDM)乘法和加法的 attention 函数。在我们的实验部分中，我们展示了方程7的特征映射与全 transformer 的性能相当，同时显著降低了计算和内存需求。

3.3. Causal Masking 因果掩码

         transformer 架构可以通过掩码 attention 计算，使第 i 个位置只受 位置 j 的影响，当且仅当

j <= i , 即某个位置不受后续位置的影响，从而可以有效地训练自回归模型。公式化，这个因果掩码将方程3变为如下：

         按照§3.2的推理，我们将被掩码的 attention 线性化，如下所述，

         通过如下引入和 ：

         简化公式9 为：

        注意，和可以在常数时间内从和计算出来，因此使得带有因果掩码的 linear transformers 的计算复杂度与序列长度成线性关系。

 3.3.1. GRADIENT COMPUTATION 梯度计算

        在任何深度学习框架中，方程12的简单实现都需要存储所有中间值，以便计算梯度。这会使内存消耗增加 max (D, M) 倍; 从而阻碍了 causal linear attention 对较长序列或较深模型的适用性。为了解决这个问题，我们推导 公式9中分子的梯度作为累加（ cumulative）和。这使我们能够计算 linear time  和 constant memory 中 causal linear attention 的前向和后向传播。补充材料中提供了详细的推导过程。

        给定分子  和标量损失函数对分子 的梯度，我们推导 如下:

        公式 9,13 -15 中的累积和项是在线性时间内计算的，并且相对于序列长度需要 constant memory 。这导致了给定的C维特征图，一个算法的计算复杂度 O(NCM) 和内存O(N max (C, M)) 。算法 1 给出了分子前后传递的伪代码实现。

 3.3.2. TRAINING AND INFERENCE 训练和推理

        当训练一个自回归 transformer 模型时，完整的 ground truth 序列是可用的。这使得 方程1 的和注意力计算都可以实现分层并行。因此，transformer 的训练比循环神经网络更高效。另一方面，在推理期间，时间步(timestep) i  的输出是 timestep i + 1 的输入。这使得自回归模型不可能并行化。此外，transformer 的每步时间成本不是恒定的; 相反，它按照当前序列长度的平方进行缩放，因为必须计算 先前所有时间步的attention。

        我们提出的 linear transformer 模型结合了两者的优点。当涉及到训练时，计算可以被并行化，并充分利用gpu或其他加速器。当涉及到推理时，每次预测的成本和内存对于我们的模型是恒定的。这意味着我们可以简单地存储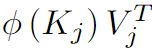矩阵作为一个内部状态，并像循环神经网络一样在每一步更新它。这导致推理速度比其他 transformer  模型快数千倍。

3.4. Transformers are RNNs

        在文献中，transformer 模型被认为是一种完全不同于递归神经网络的方法。然而，从§3.3中的因果掩码公式和上一节的讨论，很明显，任何带有因果掩码的 transformer 层可以被写为一个模型，给定输入，修改内部状态，然后预测输出，即一个循环神经网络(RNN)。请注意，与 通用Transformers（ Universal Transformers）(Dehghani et al.2018)相比，我们考虑的是时间而不是深度的循环。

        在下面的方程中，我们将方程 1 的transformer 层公式化为递归神经网络。得到的RNN有两个隐藏状态，即注意力记忆（ attention memory）s  和标准化（ normalizer）记忆 z 。我们使用下标表示循环中的时间步。

        其中， ，  分别表示表示某一 transformer 层的第 i 个输入和第 i 个输出。请注意，我们的公式没有对特征函数施加任何约束，它可以用于表示任何 transformer 模型，在理论上甚至是使用 softmax attention 的 transformer  模型。这个公式是朝着更好地理解 transformer 和流行的循环网络(Hochreiter & Schmidhuber, 1997) 以及用于存储和检索信息的过程之间的关系迈出的第一步。

4. 实验

待续