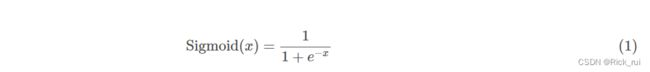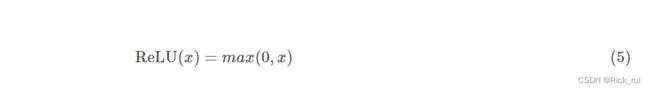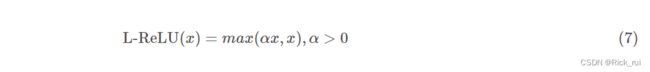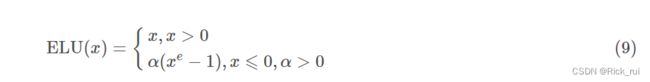通用化BP神经网络-激活函数
学习来源:日撸 Java 三百行(71-80天,BP 神经网络))_闵帆的博客-CSDN博客
1. 激活函数与求导式
激活函数是改变BP神经网络线性特征的转换函数, 是用于forward进行预测的关键一步. 而求导是通过激活函数得到的最终结果与目标值的偏差的偏导, 这个求导目标是边权, 但是通过链式法则, 最终会影响到对激活函数的求导.
1.1 Sigmod函数
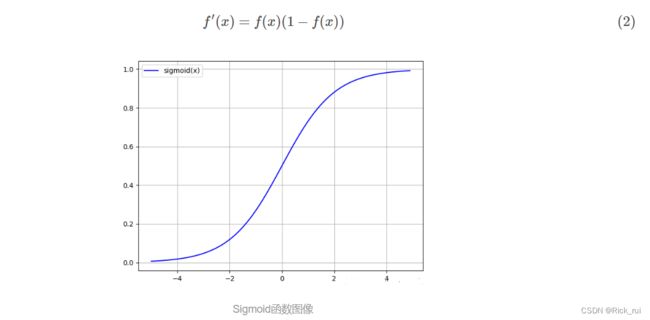
Sigmoid的导函数:
定义域为(−∞,+∞), 值域为(0,1), 随着定义域取值的变大, 函数图像不断趋近于1, 而随着定义域的缩小逐步趋近于0. 函数图像在靠近定义域中心0时速度变快, 但是分散到两端相对平滑.
Sigmoid是比较常见于许多介绍BP神经网络文章中的激活函数(可能是算式简单?), 但是通过简单的查阅, 得知Sigmoid并不是一个最好的激活函数.
- 首先Sigmoid在函数值接近饱和时候, 因为曲线减缓, 导致导数接近0, 通过若干链式组合后的数学式子中得到的最终值可能会被导数过小值特性干扰.---- 梯度消失(gradient vanishing)现象
- Sigmoid存在方向的捆绑, 难以跳出局部的解. 因此Sigmoid的值域并不沿着0对称(zero-centered), 所以后层的神经元的输入是非0均值, 这对于梯度来说有一个基本的定式逻辑: 以f=Sigmoid(wx+b)为例, 对w求导后的结果与输入值是同正负的. 这样效果直接的效果就是梯度下降存在捆绑, 反向传播过程中要么都往正方向更新,要么都往负方向更新. 这会减缓收敛, 出现锯齿形下降.
- 幂运算耗时
激活函数(函数activate)的代码部分:
switch (activator) {
//...
case SIGMOID:
resultValue = 1 / (1 + Math.exp(-paraValue));
break;
default:
System.out.println("Unsupported activator: " + activator);
System.exit(0);
}// Of switch
求导部分封装(函数derive)
switch (activator) {
//...
case SIGMOID:
resultValue = paraActivatedValue * (1 - paraActivatedValue);
break;
default:
System.out.println("Unsupported activator: " + activator);
System.exit(0);
}// Of switch
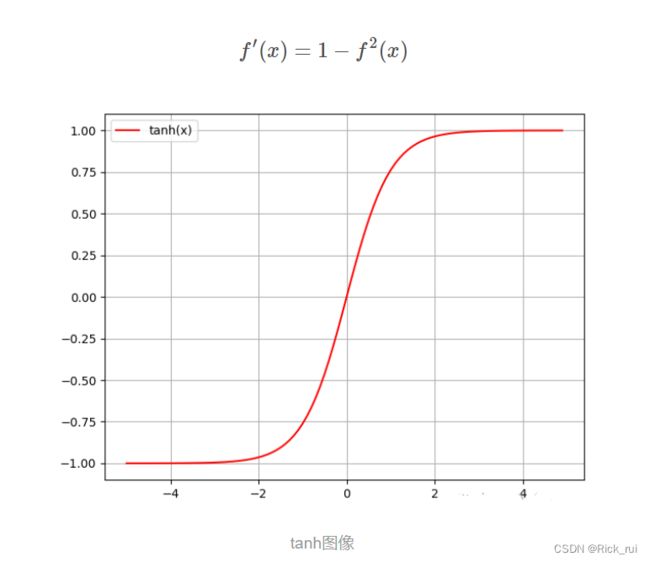
1.2 Tanh函数
有导数
定义域为(−∞,+∞), 值域为(−1,1), 随着定义域取值的变大, 函数图像不断趋近于1, 而随着定义域的缩小逐步趋近于-1. 函数图像在靠近定义域中心0时速度变快, 但是分散到两端相对平滑. (这段描述和Sigmoid基本一样啊!)
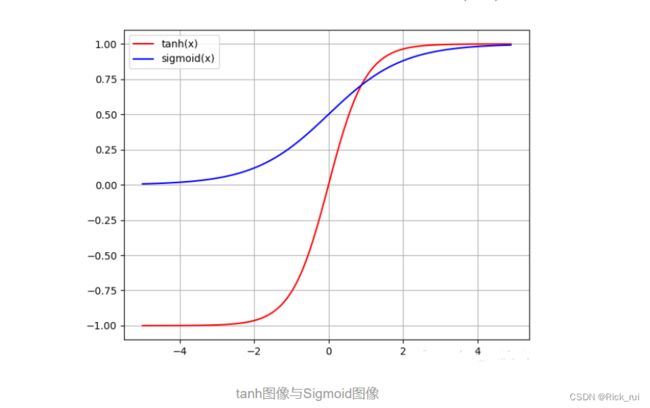
就函数来看, 这个图像非常像Sigmoid, 只不过在值域设置上相比Sigmoid, 定义域左半轴的函数图像落入了负区域, 这样使得结点取值的变化范围极大地提高了, 这是相比Sigmoid的优点, 即zero-centered中心化数据. 让均值接近于0, 而不是0.5, 这几乎让tanh可以胜任许多除了输出层以外的各种场合. 输出层的激活函数设置要视情况而定, 若我们希望的目标y位于(0,1), 那么就选Sigmoid.
本质来说, tanh其实可以通过Sigmoid变换得到: tanh(x)=2sigmoid(2x)−1
所以很多曲线层面的缺陷tanh也有哟. tanh函数值接近饱和时候的照样会曲线减缓, 导数接近0, 影响链式组合后的数学式子, 存在显而易见的梯度消失(gradient vanishing)现象. 而且tanh的幂运算依旧很多.
1.3 ReLU函数
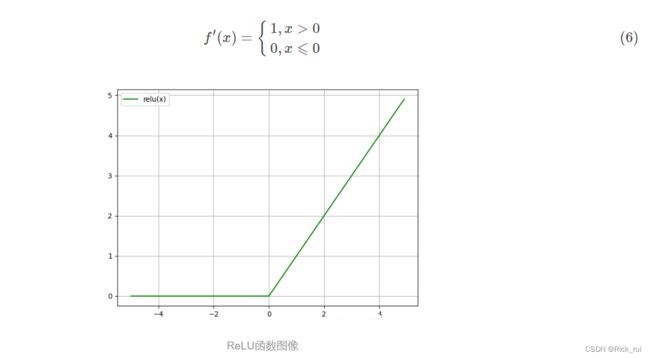
定义域为(−∞,+∞), 值域为(0,1), 随着定义域取值的变大, 函数图像不断趋近于+∞, 而定义域进入负数域, 值域保持0不变.
ReLU(Rectified Linear Units)函数的全称为修正线性单元, 是一种分段线性函数, 其弥补了sigmoid函数以及tanh函数的梯度消失问题(很明显, 后面都成正比例函数了)。而且计算复杂度非常低, 没有开销大的幂指数运算. 并且适合backPropagation(他的导数是一个类sgn函数) 此外因为她很简单, 而且分段呈现线性, 因此ReLU也容易学习和优化(一大堆基于ReLU的扩展版本)
但是ReLU也有些比较出名的缺陷:
- 首先输出不是zero-centered. 这一点只要之前看懂了1.1与1.2那便不难得出.
- 可能会因为参数的不合理初始化, 或者梯度下降因子设置过大导致下降幅度过大导致的神经元坏死现象(Dead ReLU Problem). 即某些神经元可能会被置0, 后续学习过程中它将永远无法被激活, 有关边权也永远不会更新(这很自然, 因为定义域一旦不小心变成0你就给人家一棒子敲死了) 可以采用如下办法调节 (1.Xavier初始化方法 2.别把梯度下降因子设置得太大 3.adagrad自动调节梯度下降因子)
- ReLU并不满足形如Sigmoid与Tanh等 这样的" 挤压函数(squashing function) ", 挤压函数可以把较大范围变化的数据挤压到一个有界的值域空间, 即幅度压缩. 幅度压缩应当是限制数据大小的一个很有效的方法, ReLU显然并不具备这样特性.
这里提一句, 关于Dead ReLU问题也许可以辩证看待, 当部分神经元输出为0时, 直观造成网络的稀疏性, 减少了参数相互依存的关系, 某种意义上也缓解了过拟合的发生. 这也是为什么有些改进后的ReLU在削减了负半轴一味取零的特性后还是存在比不过原算法的情况.
1.4 ReLU函数变体
1.4.1 Leakly ReLU
求导后
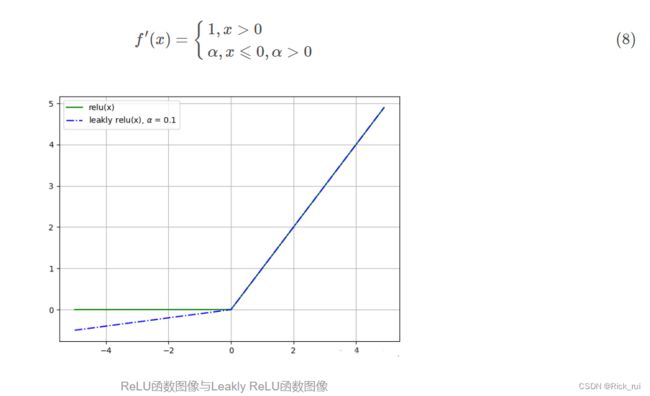
L-ReLU函数的负半轴不再是固定的0值, 而是存在一个基于α斜率控制的线性变化, 往往来说α都设置一些相对较小的值(0<α<1), 保证了负半轴的速率要弱于正半轴.
因为左半部分不再一味设0, 故可以基本解决Dead ReLU问题, 但是本身的不对称性让其无法有效保证zero-centered特性. Leakly ReLU不一定优于ReLU.
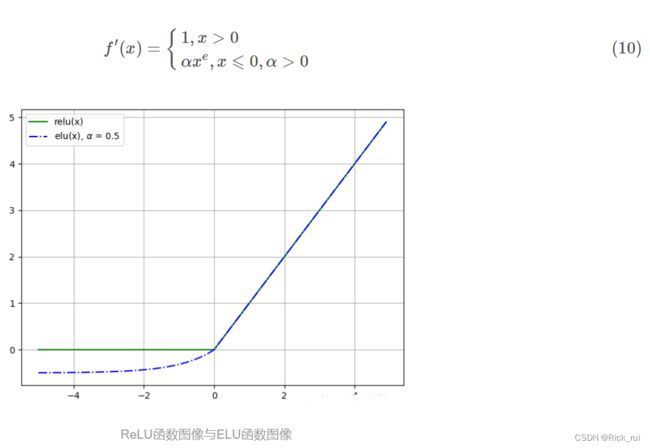
1.4.2 ELU
求导后
ELU(The exponential Linear Units)函数的全称为指数化线性单元, 继承与L-ReLU, 因此不会有Dead ReLU 问题, 而且均值可以保证足够接近0(zero-centered). 但是出现了指数部分, 有一定的计算量, 表现也不一定优于ReLU.
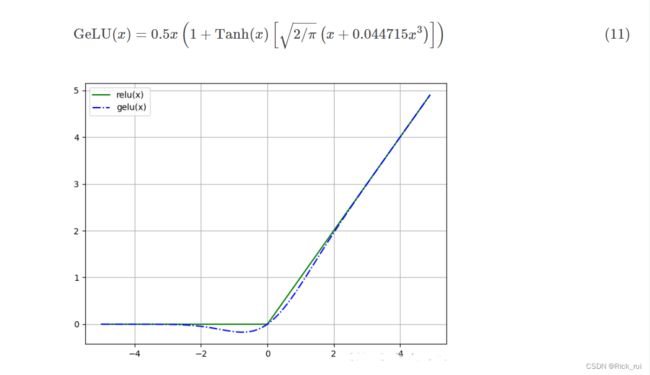
1.4.3 GeLU
了解即可
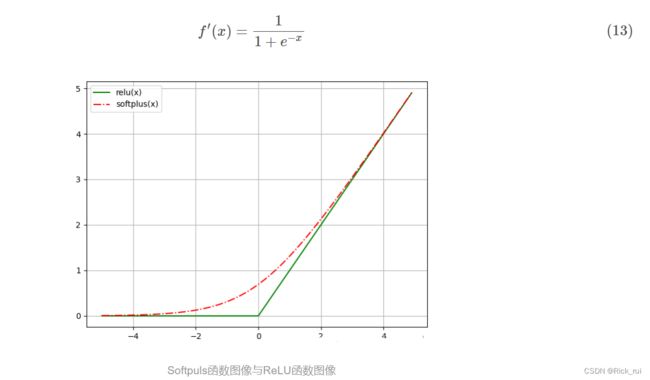
1.5 Softplus函数
求导后
定义域为(−∞,+∞), 值域为(0,1), 随着定义域取值的变大, 函数图像不断趋近于+∞, 定义域进入负数域, 取值不断趋近于0.
直观可见, Softplus似乎宛如ReLU的平滑版本, 而且负半轴并没有一味的0取值也能很好避免Dead ReLU问题. 但是引入了指数和对数, 而且求导式中有除法, 所以计算的开销仍然是存在的.
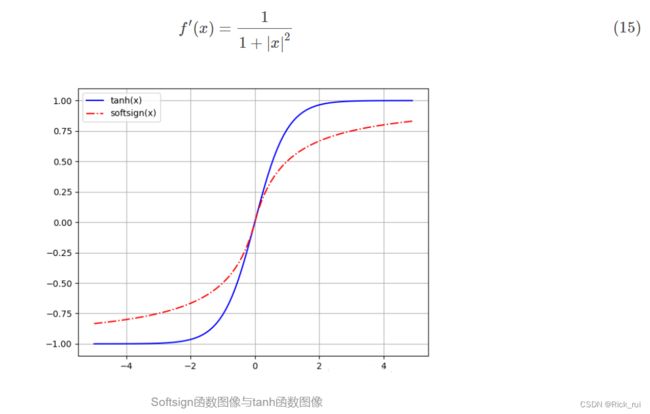
1.6 Softsign函数
求导后
定义域为(−∞,+∞), 值域为(−1,1), 随着定义域取值的变大, 函数图像不断趋近于1, 而随着定义域的缩小逐步趋近于-1. 函数图像在靠近定义域中心0时速度变快, 但是分散到两端相对平滑.很显然, Softsign是基于tanh激活函数的改造, 最明显的区别就是在当函数饱和时, Softsign就像他的名字那样, 显得更加" Soft ". 能在一定程度上避免两端因为导数过于趋近0导致的梯度消失(gradient vanishing)现象.
总之, 是Tanh的不错的代替选项.
激活函数封装代码
/**
* Alpha for elu, relu, leakly relu.
*/
double alpha;
/**
*********************
* The first constructor.
*
* @param paraActivator
* The activator.
*********************
*/
public Activator(char paraActivator) {
activator = paraActivator;
}// Of the first constructor
/**
*********************
* Setter.
*********************
*/
public void setActivator(char paraActivator) {
activator = paraActivator;
}// Of setActivator
/**
*********************
* Getter.
*********************
*/
public char getActivator() {
return activator;
}// Of getActivator
/**
*********************
* Setter.
*********************
*/
void setAlpha(double paraAlpha) {
alpha = paraAlpha;
}// Of setAlpha
/**
*********************
* Activate according to the activation function.
*********************
*/
public double activate(double paraValue) {
double resultValue = 0;
switch (activator) {
case ARC_TAN:
resultValue = Math.atan(paraValue);
break;
case ELU:
if (paraValue >= 0) {
resultValue = paraValue;
} else {
resultValue = alpha * (Math.exp(paraValue) - 1);
} // Of if
break;
case IDENTITY:
resultValue = paraValue;
break;
case LEAKY_RELU:
if (paraValue >= 0) {
resultValue = paraValue;
} else {
resultValue = alpha * paraValue;
} // Of if
break;
case SOFT_SIGN:
if (paraValue >= 0) {
resultValue = paraValue / (1 + paraValue);
} else {
resultValue = paraValue / (1 - paraValue);
} // Of if
break;
case SOFT_PLUS:
resultValue = Math.log(1 + Math.exp(paraValue));
break;
case RELU:
if (paraValue >= 0) {
resultValue = paraValue;
} else {
resultValue = 0;
} // Of if
break;
case SIGMOID:
resultValue = 1 / (1 + Math.exp(-paraValue));
break;
case TANH:
resultValue = 2 / (1 + Math.exp(-2 * paraValue)) - 1;
break;
default:
System.out.println("Unsupported activator: " + activator);
System.exit(0);
}// Of switch
return resultValue;
}// Of activate
/**
*********************
* Derive according to the activation function. Some use x while others use
* f(x).
*
* @param paraValue
* The original value x.
* @param paraActivatedValue
* f(x).
*********************
*/
public double derive(double paraValue, double paraActivatedValue) {
double resultValue = 0;
switch (activator) {
case ARC_TAN:
resultValue = 1 / (paraValue * paraValue + 1);
break;
case ELU:
if (paraValue >= 0) {
resultValue = 1;
} else {
resultValue = alpha * Math.exp(paraValue);
} // Of if
break;
case IDENTITY:
resultValue = 1;
break;
case LEAKY_RELU:
if (paraValue >= 0) {
resultValue = 1;
} else {
resultValue = alpha;
} // Of if
break;
case SOFT_SIGN:
if (paraValue >= 0) {
resultValue = 1 / (1 + paraValue) / (1 + paraValue);
} else {
resultValue = 1 / (1 - paraValue) / (1 - paraValue);
} // Of if
break;
case SOFT_PLUS:
resultValue = 1 / (1 + Math.exp(-paraValue));
break;
case RELU: // Updated
if (paraValue >= 0) {
resultValue = 1;
} else {
resultValue = 0;
} // Of if
break;
case SIGMOID: // Updated
resultValue = paraActivatedValue * (1 - paraActivatedValue);
break;
case TANH: // Updated
resultValue = 1 - paraActivatedValue * paraActivatedValue;
break;
// case SWISH:
// resultValue = ?;
// break;
default:
System.out.println("Unsupported activator: " + activator);
System.exit(0);
}// Of switch
return resultValue;
}// Of derive
/**
*********************
* Overrides the method claimed in Object.
*********************
*/
public String toString() {
String resultString = "Activator with function '" + activator + "'";
resultString += "\r\n alpha = " + alpha + ", beta = " + beta + ", gamma = " + gamma;
return resultString;
}// Of toString
/**
********************
* Test the class.
********************
*/
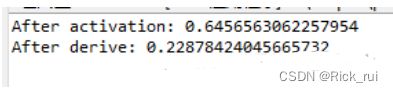
public static void main(String[] args) {
Activator tempActivator = new Activator('s');
double tempValue = 0.6;
double tempNewValue;
tempNewValue = tempActivator.activate(tempValue);
System.out.println("After activation: " + tempNewValue);
tempNewValue = tempActivator.derive(tempValue, tempNewValue);
System.out.println("After derive: " + tempNewValue);
}// Of main
}// Of class Activator测试结果如下: