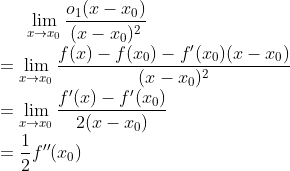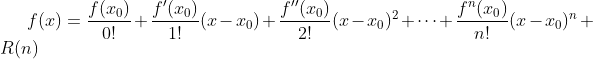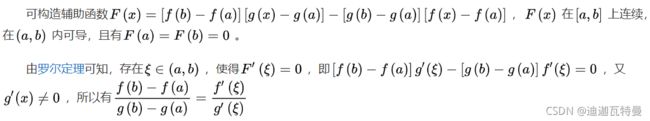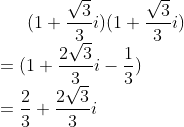欧拉公式——宇宙第一公式
目录
概述
一、泰勒公式
1. 从一阶泰勒公式说起
2. 一阶到二阶
3. 洛必达法则
4. 泰勒中值定理(泰勒公式)范式
5. 柯西中值定理
二、欧拉公式
1. 证明
2. 在复平面单位圆上的点可以用三角函数来表示
3. 复平面上乘法的几何意义
4. 对同一个点不同的描述方式
5. 为什么 是圆周运动
6. 欧拉恒等式
概述
欧拉公式是数学里最令人着迷的公式之一,它将数学里最重要的几个常数联系到了一起:两个超越数:自然对数的底e,圆周率π;两个单位:虚数单位i和自然数的单位1,以及数学里常见的0。
由于欧拉公式的证明,需要了解一个重要的公式——泰勒公式,所以在介绍欧拉公式之前,我们先聊一下泰勒公式:
一、泰勒公式
泰勒公式虽然形式不算复杂,但几乎所有的教材都是直接给出这个公式,然后再进行相应的结论证明,显得过于突兀,也不便于理解。尝试给出一种由基本的导数公式和极限定理推导泰勒公式的方法,希望能对读者诸君有所帮助。
1. 从一阶泰勒公式说起
我们首先从一阶导数着手。假设 ![]() 在
在 ![]() 有一阶导数,那么根据定义,就有
有一阶导数,那么根据定义,就有
现在回顾一下关于函数极限的一个结论:
![]() (2)
(2)
其中, ![]() 是该极限过程下的某个无穷小,即
是该极限过程下的某个无穷小,即![]() 利用这个结论,可以将 改写为
利用这个结论,可以将 改写为
其中 再进一步变形,就可得到[1]
![]() (4)
(4)
注意到(4)末尾那一项,很清楚,它是![]() 的高阶无穷小,这是因为
的高阶无穷小,这是因为
于是,我们可以直接将它记作
![]() (6)
(6)
这样的话, 式可进一步改写为
![]() (7)
(7)
好了!这就是一阶泰勒公式。
2. 一阶到二阶
那么如何得到二阶的呢?
先比较一下二阶泰勒和一阶泰勒形式上的差别吧。它们前两项都是一样的,只不过二阶的又多出了一项。注意到,高阶无穷小的记号实际上是一个「收纳筐」,它里面装着很多隐藏着的东西。如此,我们猜测,二阶泰勒多出来的这一项,一定是从一阶泰勒那个高阶无穷小中「分析」出来的。
这启发我们来考察这样一个极限
这是一个 的极限,要求解它可以考虑使用洛必达。但是,请注意,我们现在只有 在
一点一阶可导的条件,这还不足以让我们使用洛必达。不过,这并没有太大困难,只要加强条件就行,比如:我们让 ![]() 在 二阶可导,这样的话,就不仅保证了
在 二阶可导,这样的话,就不仅保证了 ![]() 存在,还同时保证了
存在,还同时保证了 ![]() 在
在 ![]() 某邻域内一阶可导,这就满足了洛必达的使用条件。
某邻域内一阶可导,这就满足了洛必达的使用条件。
3. 洛必达法则
洛必达法则(l'Hôpital's rule)是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。大意为两个无穷小之比或两个无穷大之比的极限可能存在,也可能不存在。因此,求这类极限时往往需要适当的变形,转化成可利用极限运算法则或重要极限的形式进行计算。洛必达法则便是应用于这类极限计算的通用方法。这法则是由瑞士数学家约翰·伯努利(Johann Bernoulli)所发现的,因此也被叫作伯努利法则(Bernoulli's rule)。
不严格的说,洛必达法则就是在 ![]() 型和
型和 ![]() 型时,有
型时,有
展开来说洛必达(L 'Hopital)法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
洛必达法则(定理)
设函数![]() 和
和![]() 满足下列条件:
满足下列条件:
⑴![]() 时,
时,![]() ,
,![]() ;
;
⑵在点a的某去心邻域内![]() 与
与![]() 都可导,且
都可导,且![]() 的导数不等于0;
的导数不等于0;
⑶![]() 时,
时,![]() 存在或为无穷大
存在或为无穷大
则![]() 时,
时,![]()
好了!开始洛必达!
现在,我们又利用 的结论,将这个极限改写为
基于同样的理由, ![]() 我们将它代入 并连同 一起代回 (10) ,就将得到
我们将它代入 并连同 一起代回 (10) ,就将得到
很清楚,这就是二阶泰勒公式!
4. 泰勒中值定理(泰勒公式)范式
![]() 由导数的定义可知,当函数
由导数的定义可知,当函数![]() 在点
在点![]() 处可导时,在点
处可导时,在点![]() 的邻域
的邻域![]() 内恒有
内恒有
![]()
因为![]() 是一个无穷小量,故有
是一个无穷小量,故有![]()
这是在对函数进行局部线性化处理时常用的公式之一。从几何上看,它是用切线近似代替曲线。然而,这样的近似是比较粗糙的,而且只在点的附近才有近似意义。为了改善上述不足,使得近似替代更加精密,数学家们在柯西中值定理的基础上,推导出了泰勒中值定理(泰勒公式)
若函数![]() 在包含
在包含![]() 的某个开区间(a,b)上具有(n+1)阶的导数,那么对于任一
的某个开区间(a,b)上具有(n+1)阶的导数,那么对于任一![]() ,有
,有
其中,![]() ,此处的
,此处的![]() 为
为![]() 与
与![]() 之间的某个值。
之间的某个值。![]() 的成为n阶泰勒公式,其中,
的成为n阶泰勒公式,其中,![]() 称为n次泰勒多项式,它与
称为n次泰勒多项式,它与![]() 的误差,
的误差,![]() 成为n阶泰勒余项。
成为n阶泰勒余项。
5. 柯西中值定理
柯西中值定理,是著名的数学定理,证明了微积分学基本定理即牛顿-莱布尼茨公式。利用定积分严格证明了带余项的泰勒公式,还用微分与积分中值定理表示曲边梯形的面积,推导了平面曲线之间图形的面积、曲面面积和立体体积的公式。简单地理解,就是初中以及高中了解到的斜率与导数的关系。函数在某点的斜率等于该函数在该点的导数。
柯西中值定理是拉格朗日中值定理的推广,是微分学的基本定理之一。其几何意义为,用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。该定理可以视作在参数方程下拉格朗日中值定理的表达形式。柯西中值定理粗略地表明,对于两个端点之间的给定平面弧,至少有一个点,使曲线在该点的切线平行于两端点所在的弦。
二、欧拉公式
这个发表于公元1748年的数学公式,将三角函数与复指数函数巧妙地关联了起来。
![]()
其中, ![]() 为自然常数,
为自然常数, ![]() 为虚数,
为虚数, ![]() 则是以弧度为单位的参数(变量)。
则是以弧度为单位的参数(变量)。
1. 证明
根据泰勒公式展开
当![]() 时,有
时,有
![]()
2. 在复平面单位圆上的点可以用三角函数来表示
![]()
![]()
3. 复平面上乘法的几何意义
![]()
![]()
证明:
既坐标由![]() ,变为
,变为![]() ,由三角函数定理得知,移动后的模长为之前的2倍,角度由
,由三角函数定理得知,移动后的模长为之前的2倍,角度由![]() 以原点旋转
以原点旋转![]() ,变为
,变为![]() 。
。
4. 对同一个点不同的描述方式
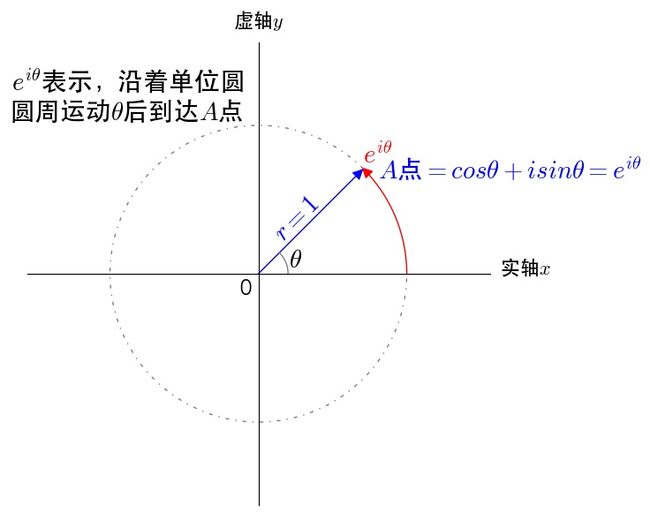 5. 为什么
5. 为什么  是圆周运动
是圆周运动
e,作为数学常数,是自然对数函数的底数。有时称它为欧拉数,以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔 引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。![]() 定义为:
定义为:![]()
这是实数域上的定义,可以推广到复数域 ![]() ,根据之前对复数乘法的描述,乘上
,根据之前对复数乘法的描述,乘上![]() 是进行伸缩和旋转运动,
是进行伸缩和旋转运动, ![]() 取值不同,伸缩和旋转的幅度不同
取值不同,伸缩和旋转的幅度不同
![]()
三角函数定义域被扩大到了复数域,我们把复数当作向量来看待,复数的实部是![]() 方向,虚部是
方向,虚部是 ![]() 方向,很容易观察出其几何意义。
方向,很容易观察出其几何意义。
![]()
![]()
6. 欧拉恒等式
当![]() 时,带入欧拉公式:
时,带入欧拉公式:
![]() ,这就是就是欧拉恒等式,被誉为上帝公式。
,这就是就是欧拉恒等式,被誉为上帝公式。![]() 、
、![]() 、
、![]() 、乘法单位元1、加法单位元0,这五个重要的数学元素全部被包含在内,在数学爱好者眼里,仿佛一行诗道尽了数学的美好。
、乘法单位元1、加法单位元0,这五个重要的数学元素全部被包含在内,在数学爱好者眼里,仿佛一行诗道尽了数学的美好。