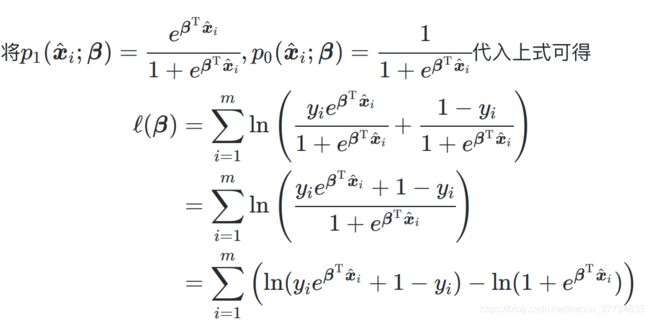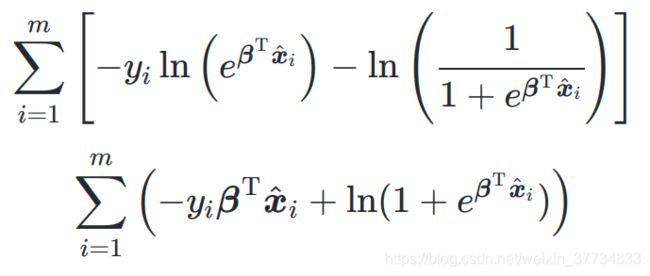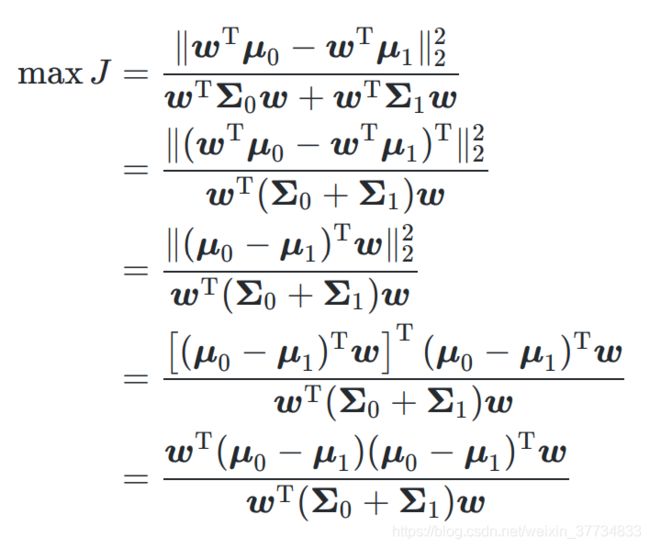- 机器学习之条件概率
贾斯汀玛尔斯
2024最新深度学习算法机器学习人工智能
1.引言概率模型在机器学习中广泛应用于数据分析、模式识别和推理任务。本文将调研几种重要的概率模型,包括EM算法、MCMC、朴素贝叶斯、贝叶斯网络、概率图模型(CRF、HMM)以及最大熵模型,介绍其基本原理、算法流程、应用场景及优势。2.EM算法(Expectation-Maximization)2.1概述EM算法是一种用于含有隐变量或缺失数据的最大似然估计方法。其核心思想是交替执行期望(E)步骤和
- 从零开始学AI——1
人工智能
前言最近总算有想法回到学习上来,这次就拿AI开刀吧。本系列叫从零开始学AI不是骗人的,我对AI的了解几乎就是道听途说,所以起了这么一个标题,希望学完从0变1(?此外,我应该不会特别关注代码实现上的内容,因为我对python也是一窍不通。本笔记为学习周志华老师《机器学习》(西瓜书)的个人学习记录,内容基于个人理解进行整理和再阐述。由于理解可能存在偏差,欢迎指正。引用模块说明:在笔记中,我会使用引用模
- Python 学习 第五册 深度学习 第1章 什么是深度学习
weixin_38135241
python学习深度学习人工智能
----用教授的方式学习。目录1.1人工智能、机器学习与深度学习1.1.1人工智能1.1.2机器学习1.1.3从数据中学习表示1.1.4深度学习之“深度”1.1.5用三张图理解深度学习的工作原理1.2深度学习之前:机器学习简史1.2.1概率建模1.2.2核方法1.2.3决策树、随机森林与梯度提升机1.2.4深度学习有何不同什么是深度学习?1.1人工智能、机器学习与深度学习三者关系:1.1.1人工智
- 珍藏!Java SpringBoot 精品源码合集约惠来袭,获取路径大公开
秋野酱
javaspringboot开发语言
技术范围:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app、大数据、物联网、机器学习等设计与开发。主要内容:免费功能设计、开题报告、任务书、中期检查PPT、系统功能实现、代码编写、论文编写和辅导、论文降重、长期答辩答疑辅导、腾讯会议一对一专业讲解辅导答辩、模拟答辩演练、和理解代码逻辑思路。文末获取源码联系文末获取源码联
- 机器学习驱动的智能化电池管理技术与应用
满木悦
电池化学机器人化学电池机器学习人工智能硕博研究生
在人工智能与电池管理技术融合的背景下,电池科技的研究和应用正迅速发展,创新解决方案层出不穷。从电池性能的精确评估到复杂电池系统的智能监控,从数据驱动的故障诊断到电池寿命的预测优化,人工智能技术正以其强大的数据处理能力和模式识别优势,推动电池管理领域的技术进步。据最新研究动态,目前在电池管理领域的人工智能应用主要集中在以下几个方面:1.状态估计:包括电池的荷电状态(SOC)和健康状态(SOH)的实时
- 梯度下降法理论理解
伶星37
机器学习人工智能
梯度下降法:看似原始却透露着机器学习的本质前提:在研究梯度下降方法之前,你要理解矩阵运算(解析解)的方法矩阵运算目前的缺点只能进行对线性函数经行分析,无法对复杂的函数经行分析什么是梯度,以及梯度向量梯度下降的形象例子以及基本思想有三个兄弟被困在山上,得要死,他们目标是看谁尽快找到山谷中的水源老大比较后选择最陡的方向随便探索一下,就朝较低处走去探测几下就走陡峭的方向梯度下降算法的核心思想就是沿着负梯
- Java 大视界 -- 基于 Java 的大数据机器学习模型的多模态融合技术与应用(143)
青云交
大数据新视界Java大视界java大数据机器学习多模态融合智能安防智能客服数据处理
亲爱的朋友们,热烈欢迎来到青云交的博客!能与诸位在此相逢,我倍感荣幸。在这飞速更迭的时代,我们都渴望一方心灵净土,而我的博客正是这样温暖的所在。这里为你呈上趣味与实用兼具的知识,也期待你毫无保留地分享独特见解,愿我们于此携手成长,共赴新程!一、欢迎加入【福利社群】点击快速加入:青云交灵犀技韵交响盛汇福利社群点击快速加入2:2024CSDN博客之星创作交流营(NEW)二、本博客的精华专栏:大数据新视
- 2025年第二届机器学习与神经网络国际学术会议(MLNN 2025)
分享学术科研与论文的禁小默
机器学习神经网络人工智能
重要信息官网:www.icmlnn.org时间:2025年4月22-24日地点:中国-重庆简介2025年第二届机器学习与神经网络国际学术会议(MLNN2025)围绕学习系统与神经网络的核心理论、关键技术和应用展开讨论,涵盖深度学习、计算机视觉、自然语言处理、强化学习等多个子领域,通过特邀报告、主题演讲、海报展示等形式,展示相关领域的最新研究成果和技术创新。征稿主题神经网络机器学习深度学习算法及应用
- MySQL中基于机器学习的自适应缓存热点识别优化策略——开启数据库性能新纪元
墨夶
数据库学习资料1数据库mysql机器学习
在数据驱动的世界里,数据库的性能直接影响到整个应用系统的响应速度和用户体验。随着业务量的增长和技术的发展,传统的缓存机制逐渐暴露出局限性。如何更智能地识别并利用热点数据进行缓存优化,成为提升数据库性能的关键所在。今天,我们将深入探讨一种创新的方法——基于机器学习的自适应缓存热点识别优化策略,并分享其在MySQL中的具体实现方案。为什么选择机器学习?传统上,开发者们依赖于手动配置或预设规则来决定哪
- AI人工智能软件开发方案:开启智能时代的创新钥匙
广州硅基技术官方
人工智能
一、引言:AI浪潮下的软件开发新机遇近年来,人工智能(AI)技术的迅猛发展如同一股汹涌澎湃的浪潮,席卷了全球各个领域。从最初的概念提出到如今的广泛应用,AI历经了漫长的发展历程,终于迎来了属于它的黄金时代。回首过去,AI的发展并非一帆风顺,早期由于计算能力和算法的限制,经历了多次起伏。但随着大数据、云计算、机器学习、深度学习等技术的不断突破,AI迎来了爆发式增长。如今,AI已经深入到人们生活和工作
- 【机器学习】算法分类
CH3_CH2_CHO
什么?!是机器学习!!机器学习算法有监督学习无监督学习半监督学习强化学习
1、有监督学习1.1定义使用带标签的数据训练模型。有监督学习是机器学习中最常见的一种类型,它利用已知的输入特征和对应的输出标签来训练模型,使模型能够学习到特征与标签之间的映射关系。在训练过程中,模型会不断地调整自身的参数,以最小化预测值与真实标签之间的误差,从而提高预测的准确性。1.2回归问题1.2.1目标预测连续值。回归问题的目标是预测一个连续的数值结果,模型的输出是一个实数值。1.2.2解释回
- 使用 Baseten 部署和运行机器学习模型的指南
shuoac
机器学习人工智能python
随着机器学习模型在各个行业中的广泛应用,如何高效地部署和运行这些模型成为一个关键问题。本文将介绍如何使用Baseten平台来部署和服务机器学习模型。Baseten是LangChain生态系统中的一个重要提供者,它提供了所需的基础设施来高效地运行模型。无论是开源模型如Llama2和Mistral,还是专有或经过微调的模型,Baseten都能在专用GPU上运行。技术背景介绍Baseten提供了一种不同
- 机器学习——分类、回归、聚类、LASSO回归、Ridge回归(自用)
代码的建筑师
模型学习模型训练机器学习机器学习分类回归正则化项LASSORidge朴素
纠正自己的误区:机器学习是一个大范围,并不是一个小的方向,比如:线性回归预测、卷积神经网络和强化学都是机器学习算法在不同场景的应用。机器学习最为关键的是要有数据,也就是数据集名词解释:数据集中的一行叫一条样本或者实例,列名称为特征或者属性。样本的数量称为数据量,特征的数量称为特征维度机器学习常用库:Numpy和sklearn朴素的意思是特征的各条件都是相互独立的机器学习(模型、策略、算法)损失函数
- 量化交易系统中如何处理机器学习模型的训练和部署?
openwin_top
量化交易系统开发机器学习人工智能量化交易
microPythonPython最小内核源码解析NI-motion运动控制c语言示例代码解析python编程示例系列python编程示例系列二python的Web神器Streamlit如何应聘高薪职位量化交易系统中,机器学习模型的训练和部署需要遵循一套严密的流程,以确保模型的可靠性、性能和安全性。以下是详细描述以及相关的示例:1.数据收集和预处理数据收集在量化交易中,数据是最重要的资产。收集的数
- 【深度学习与大模型基础】第7章-特征分解与奇异值分解
lynn-66
深度学习与大模型基础算法机器学习人工智能
一、特征分解特征分解(EigenDecomposition)是线性代数中的一种重要方法,广泛应用于计算机行业的多个领域,如机器学习、图像处理和数据分析等。特征分解将一个方阵分解为特征值和特征向量的形式,帮助我们理解矩阵的结构和性质。1.特征分解的定义对于一个n×n的方阵A,如果存在一个非零向量v和一个标量λ,使得:则称λ为矩阵A的特征值,v为对应的特征向量。特征分解将矩阵A分解为:其中:Q是由特征
- 【论文阅读】Persistent Homology Captures the Generalization of Neural Networks Without A Validation Set
开心星人
论文阅读论文阅读
将神经网络表征为加权的无环图,直接根据模型的权重矩阵构造PD。计算相邻batch的权重矩阵PD之间的距离。比较同调收敛性与神经网络的验证精度变化趋势摘要机器学习从业者通常通过监控模型的某些指标来估计其泛化误差,并在训练数值收敛之前停止训练,以防止过拟合。通常,这种误差度量或任务相关的指标是通过一个验证集(holdoutset)来计算的。因为这些数据没有直接用于更新模型参数,通常假设模型在验证集上的
- 震惊! “深度学习”都在学习什么
扉间798
深度学习学习人工智能
常见的机器学习分类算法俗话说三个臭皮匠胜过诸葛亮这里面集成学习就是将单一的算法弱弱结合算法融合用投票给特征值加权重AdaBoost集成学习算法通过迭代训练一系列弱分类器,给予分类错误样本更高权重,使得后续弱分类器更关注这些样本,然后将这些弱分类器线性组合成强分类器,提高整体分类性能。(一)投票机制投票是一种直观且常用的算法融合策略。在多分类问题中,假设有多个分类器对同一数据进行分类判断。每个分类器
- 【论文阅读】Availability Attacks Create Shortcuts
开心星人
论文阅读论文阅读
还得重复读这一篇论文,有些地方理解不够透彻可用性攻击通过在训练数据中添加难以察觉的扰动,使数据无法被机器学习算法利用,从而防止数据被未经授权地使用。例如,一家私人公司未经用户同意就收集了超过30亿张人脸图像,用于构建商业人脸识别模型。为解决这些担忧,许多数据投毒攻击被提出,以防止数据被未经授权的深度模型学习。它们通过在训练数据中添加难以察觉的扰动,使模型无法从数据中学习太多信息,从而导致模型在未见
- 机器学习 Day01人工智能概述
山北雨夜漫步
机器学习人工智能
1.什么样的程序适合在gpu上运行计算密集型的程序:此类程序主要运算集中在寄存器,寄存器读写速度快,而GPU拥有强大的计算能力,能高效处理大量的寄存器运算,因此适合在GPU上运行。像科学计算中的数值模拟、密码破解等场景的程序,都属于计算密集型,在GPU上运行可大幅提升运算速度。易于并行的程序:GPU采用SIMD架构,有众多核心,同一时间每个核心适合做相同的事。易于并行的程序能充分利用GPU这一特性
- 机器学习:让计算机学会思考的艺术
平凡而伟大.
机器学习机器学习人工智能
目录什么是机器学习?机器学习的基本步骤常见的机器学习算法机器学习的实际应用如何入门机器学习?结语在当今数字化时代,机器学习(MachineLearning,ML)已经成为一个炙手可热的话题。从推荐系统到自动驾驶汽车,再到语音助手,机器学习的应用无处不在。然而,对于许多人来说,机器学习仍然是一个神秘而复杂的领域。本文将用通俗易懂的语言,带你走进机器学习的世界,了解它的基本原理和应用。什么是机器学习?
- 机器学习中的 K-均值聚类算法及其优缺点
平凡而伟大.
机器学习机器学习算法均值算法
K-均值聚类是一种常用的无监督学习算法,用于将数据集中的样本分成K个簇。其基本原理是将所有样本点划分到K个簇使得簇内样本点之间的距离尽可能接近,而不同簇之间的距离尽可能远。算法流程如下:随机选择K个样本点作为初始的聚类中心。将每个样本点分配到与其最近的聚类中心所在的簇。更新每个簇的聚类中心为该簇所有样本点的平均值。重复第2步和第3步,直到聚类中心不再变化或者达到最大迭代次数。优点:简单且易于实现。
- 一文讲清楚深度学习和机器学习
平凡而伟大.
机器学习人工智能深度学习机器学习人工智能
目录1.定义机器学习(MachineLearning,ML)深度学习(DeepLearning,DL)2.工作原理机器学习深度学习3.应用场景机器学习深度学习4.主要区别5.为什么选择深度学习?6.总结深度学习和机器学习是人工智能(AI)领域中两个密切相关但有所区别的概念。要清楚地解释它们之间的关系,我们可以从定义、工作原理、应用场景以及两者的主要区别等方面进行探讨。1.定义机器学习(Machin
- 机器学习knnlearn1
XW-ABAP
机器学习机器学习人工智能
importmatplotlib.pyplotaspltimportnumpyasnpimportoperator#定义一个函数用于创建数据集defcreateDataSet():#定义特征矩阵,每个元素是一个二维坐标点,代表不同策略数据点的坐标group=np.array([[20,3],[15,5],[18,1],[5,17],[2,15],[3,20]])#定义每个数据点对应的标签,用于区分
- 基于 MySQL 和 Spring Boot 的在线论坛管理系统设计与实现
城南|阿洋-计算机从小白到大神
mysqlspringboot数据库
markdownCopy✌全网粉丝20W+,csdn特邀作者、博客专家、CSDN[新星计划]导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、pyhton、机器学习技术领域和毕业项目实战✌哈喽兄弟们,好久不见哦~最近整理了一下之前写过的一些小项目/毕业设计。发现还是有很多存货的,想一想既然放在电脑里面也吃灰,那么还不如分享出去,没准还可以帮助到
- 零基础入门机器学习:用Scikit-learn实现鸢尾花分类
藍海琴泉
机器学习scikit-learn分类
适合人群:机器学习新手|数据分析爱好者|需快速展示案例的学生一、引言:为什么要学这个案例?目的:明确机器学习解决什么问题,建立学习信心。机器学习定义:让计算机从数据中自动学习规律(如分类鸢尾花品种)。为什么选鸢尾花数据集:数据量小、特征明确,适合教学演示。Scikit-learn优势:提供现成算法和工具,无需从头写数学公式。二、环境准备:5分钟快速上手目的:搭建可运行的代码环境,避免卡在工具安装环
- 机器学习--DBSCAN聚类算法详解
2201_75491841
机器学习算法聚类人工智能
目录引言1.什么是DBSCAN聚类?2.DBSCAN聚类算法的原理3.DBSCAN算法的核心概念3.1邻域(Neighborhood)3.2核心点(CorePoint)3.3直接密度可达(DirectlyDensity-Reachable)3.4密度可达(Density-Reachable)3.5密度相连(Density-Connected)4.DBSCAN算法的步骤5.DBSCAN算法的优缺点5
- 【机器学习】机器学习工程实战-第3章 数据收集和准备
腊肉芥末果
机器学习工程实战机器学习人工智能
上一章:第2章项目开始前文章目录3.1关于数据的问题3.1.1数据是否可获得3.1.2数据是否相当大3.1.3数据是否可用3.1.4数据是否可理解3.1.5数据是否可靠3.2数据的常见问题3.2.1高成本3.2.2质量差3.2.3噪声(noise)3.2.4偏差(bias)3.2.5预测能力低(lowpredictivepower)3.2.6过时的样本3.2.7离群值3.2.8数据泄露/目标泄漏3
- 机器学习实战 第一章 机器学习基础
LuoY、
MachineLearning机器学习算法人工智能
第一章机器学习1.1何谓机器学习1.2关键术语1.3机器学习的主要任务1.4如何选择合适的算法1.5开发机器学习应用程序的步骤1.6Python语言的优势1.1何谓机器学习 1、简单地说,机器学习就是把无序的数据转换成有用的信息; 2、机器学习能让我们自数据集中受启发,我们会利用计算机来彰显数据背后的真实含义; 3、机器学习横跨计算机科学、工程技术和统计学等多个学科,需要多学科的
- 数据挖掘实战-基于机器学习的垃圾邮件检测模型
艾派森
数据挖掘实战合集数据挖掘机器学习人工智能python
♂️个人主页:@艾派森的个人主页✍作者简介:Python学习者希望大家多多支持,我们一起进步!如果文章对你有帮助的话,欢迎评论点赞收藏加关注+目录1.项目背景2.数据集介绍
- 集成学习(随机森林)
herry57
数学建模大数据随机森林集成学习
目录一、集成学习概念二、Bagging集成原理三、随机森林四、例子(商品分类)一、集成学习概念集成学习通过建⽴⼏个模型来解决单⼀预测问题。它的⼯作原理是⽣成多个分类器/模型,各⾃独⽴地学习和作出预测。这些预测最后结合成组合预测,因此优于任何⼀个单分类的做出预测。只要单分类器的表现不太差,集成学习的结果总是要好于单分类器的二、Bagging集成原理分类圆形和长方形三、随机森林在机器学习中,随机森林是
- java数字签名三种方式
知了ing
javajdk
以下3钟数字签名都是基于jdk7的
1,RSA
String password="test";
// 1.初始化密钥
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(51
- Hibernate学习笔记
caoyong
Hibernate
1>、Hibernate是数据访问层框架,是一个ORM(Object Relation Mapping)框架,作者为:Gavin King
2>、搭建Hibernate的开发环境
a>、添加jar包:
aa>、hibernatte开发包中/lib/required/所
- 设计模式之装饰器模式Decorator(结构型)
漂泊一剑客
Decorator
1. 概述
若你从事过面向对象开发,实现给一个类或对象增加行为,使用继承机制,这是所有面向对象语言的一个基本特性。如果已经存在的一个类缺少某些方法,或者须要给方法添加更多的功能(魅力),你也许会仅仅继承这个类来产生一个新类—这建立在额外的代码上。
- 读取磁盘文件txt,并输入String
一炮送你回车库
String
public static void main(String[] args) throws IOException {
String fileContent = readFileContent("d:/aaa.txt");
System.out.println(fileContent);
- js三级联动下拉框
3213213333332132
三级联动
//三级联动
省/直辖市<select id="province"></select>
市/省直辖<select id="city"></select>
县/区 <select id="area"></select>
- erlang之parse_transform编译选项的应用
616050468
parse_transform游戏服务器属性同步abstract_code
最近使用erlang重构了游戏服务器的所有代码,之前看过C++/lua写的服务器引擎代码,引擎实现了玩家属性自动同步给前端和增量更新玩家数据到数据库的功能,这也是现在很多游戏服务器的优化方向,在引擎层面去解决数据同步和数据持久化,数据发生变化了业务层不需要关心怎么去同步给前端。由于游戏过程中玩家每个业务中玩家数据更改的量其实是很少
- JAVA JSON的解析
darkranger
java
// {
// “Total”:“条数”,
// Code: 1,
//
// “PaymentItems”:[
// {
// “PaymentItemID”:”支款单ID”,
// “PaymentCode”:”支款单编号”,
// “PaymentTime”:”支款日期”,
// ”ContractNo”:”合同号”,
//
- POJ-1273-Drainage Ditches
aijuans
ACM_POJ
POJ-1273-Drainage Ditches
http://poj.org/problem?id=1273
基本的最大流,按LRJ的白书写的
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define INF 0x7fffffff
int ma
- 工作流Activiti5表的命名及含义
atongyeye
工作流Activiti
activiti5 - http://activiti.org/designer/update在线插件安装
activiti5一共23张表
Activiti的表都以ACT_开头。 第二部分是表示表的用途的两个字母标识。 用途也和服务的API对应。
ACT_RE_*: 'RE'表示repository。 这个前缀的表包含了流程定义和流程静态资源 (图片,规则,等等)。
A
- android的广播机制和广播的简单使用
百合不是茶
android广播机制广播的注册
Android广播机制简介 在Android中,有一些操作完成以后,会发送广播,比如说发出一条短信,或打出一个电话,如果某个程序接收了这个广播,就会做相应的处理。这个广播跟我们传统意义中的电台广播有些相似之处。之所以叫做广播,就是因为它只负责“说”而不管你“听不听”,也就是不管你接收方如何处理。另外,广播可以被不只一个应用程序所接收,当然也可能不被任何应
- Spring事务传播行为详解
bijian1013
javaspring事务传播行为
在service类前加上@Transactional,声明这个service所有方法需要事务管理。每一个业务方法开始时都会打开一个事务。
Spring默认情况下会对运行期例外(RunTimeException)进行事务回滚。这
- eidtplus operate
征客丶
eidtplus
开启列模式: Alt+C 鼠标选择 OR Alt+鼠标左键拖动
列模式替换或复制内容(多行):
右键-->格式-->填充所选内容-->选择相应操作
OR
Ctrl+Shift+V(复制多行数据,必须行数一致)
-------------------------------------------------------
- 【Kafka一】Kafka入门
bit1129
kafka
这篇文章来自Spark集成Kafka(http://bit1129.iteye.com/blog/2174765),这里把它单独取出来,作为Kafka的入门吧
下载Kafka
http://mirror.bit.edu.cn/apache/kafka/0.8.1.1/kafka_2.10-0.8.1.1.tgz
2.10表示Scala的版本,而0.8.1.1表示Kafka
- Spring 事务实现机制
BlueSkator
spring代理事务
Spring是以代理的方式实现对事务的管理。我们在Action中所使用的Service对象,其实是代理对象的实例,并不是我们所写的Service对象实例。既然是两个不同的对象,那为什么我们在Action中可以象使用Service对象一样的使用代理对象呢?为了说明问题,假设有个Service类叫AService,它的Spring事务代理类为AProxyService,AService实现了一个接口
- bootstrap源码学习与示例:bootstrap-dropdown(转帖)
BreakingBad
bootstrapdropdown
bootstrap-dropdown组件是个烂东西,我读后的整体感觉。
一个下拉开菜单的设计:
<ul class="nav pull-right">
<li id="fat-menu" class="dropdown">
- 读《研磨设计模式》-代码笔记-中介者模式-Mediator
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
* 中介者模式(Mediator):用一个中介对象来封装一系列的对象交互。
* 中介者使各对象不需要显式地相互引用,从而使其耦合松散,而且可以独立地改变它们之间的交互。
*
* 在我看来,Mediator模式是把多个对象(
- 常用代码记录
chenjunt3
UIExcelJ#
1、单据设置某行或某字段不能修改
//i是行号,"cash"是字段名称
getBillCardPanelWrapper().getBillCardPanel().getBillModel().setCellEditable(i, "cash", false);
//取得单据表体所有项用以上语句做循环就能设置整行了
getBillC
- 搜索引擎与工作流引擎
comsci
算法工作搜索引擎网络应用
最近在公司做和搜索有关的工作,(只是简单的应用开源工具集成到自己的产品中)工作流系统的进一步设计暂时放在一边了,偶然看到谷歌的研究员吴军写的数学之美系列中的搜索引擎与图论这篇文章中的介绍,我发现这样一个关系(仅仅是猜想)
-----搜索引擎和流程引擎的基础--都是图论,至少像在我在JWFD中引擎算法中用到的是自定义的广度优先
- oracle Health Monitor
daizj
oracleHealth Monitor
About Health Monitor
Beginning with Release 11g, Oracle Database includes a framework called Health Monitor for running diagnostic checks on the database.
About Health Monitor Checks
Health M
- JSON字符串转换为对象
dieslrae
javajson
作为前言,首先是要吐槽一下公司的脑残编译部署方式,web和core分开部署本来没什么问题,但是这丫居然不把json的包作为基础包而作为web的包,导致了core端不能使用,而且我们的core是可以当web来用的(不要在意这些细节),所以在core中处理json串就是个问题.没办法,跟编译那帮人也扯不清楚,只有自己写json的解析了.
- C语言学习八结构体,综合应用,学生管理系统
dcj3sjt126com
C语言
实现功能的代码:
# include <stdio.h>
# include <malloc.h>
struct Student
{
int age;
float score;
char name[100];
};
int main(void)
{
int len;
struct Student * pArr;
int i,
- vagrant学习笔记
dcj3sjt126com
vagrant
想了解多主机是如何定义和使用的, 所以又学习了一遍vagrant
1. vagrant virtualbox 下载安装
https://www.vagrantup.com/downloads.html
https://www.virtualbox.org/wiki/Downloads
查看安装在命令行输入vagrant
2.
- 14.性能优化-优化-软件配置优化
frank1234
软件配置性能优化
1.Tomcat线程池
修改tomcat的server.xml文件:
<Connector port="8080" protocol="HTTP/1.1" connectionTimeout="20000" redirectPort="8443" maxThreads="1200" m
- 一个不错的shell 脚本教程 入门级
HarborChung
linuxshell
一个不错的shell 脚本教程 入门级
建立一个脚本 Linux中有好多中不同的shell,但是通常我们使用bash (bourne again shell) 进行shell编程,因为bash是免费的并且很容易使用。所以在本文中笔者所提供的脚本都是使用bash(但是在大多数情况下,这些脚本同样可以在 bash的大姐,bourne shell中运行)。 如同其他语言一样
- Spring4新特性——核心容器的其他改进
jinnianshilongnian
spring动态代理spring4依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- Linux设置tomcat开机启动
liuxingguome
tomcatlinux开机自启动
执行命令sudo gedit /etc/init.d/tomcat6
然后把以下英文部分复制过去。(注意第一句#!/bin/sh如果不写,就不是一个shell文件。然后将对应的jdk和tomcat换成你自己的目录就行了。
#!/bin/bash
#
# /etc/rc.d/init.d/tomcat
# init script for tomcat precesses
- 第13章 Ajax进阶(下)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- Troubleshooting Crystal Reports off BW
blueoxygen
BO
http://wiki.sdn.sap.com/wiki/display/BOBJ/Troubleshooting+Crystal+Reports+off+BW#TroubleshootingCrystalReportsoffBW-TracingBOE
Quite useful, especially this part:
SAP BW connectivity
For t
- Java开发熟手该当心的11个错误
tomcat_oracle
javajvm多线程单元测试
#1、不在属性文件或XML文件中外化配置属性。比如,没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中,还是UAT(用户验收
测试)环境中,都可以顺畅无阻地运行,但是一旦部署在PROD 上,把它作为多线程程序处理更大的数据集时,就会抛出IOException,原因可能是JDBC驱动版本不同,也可能是#2中讨论的问题。如果线程数目 可以在属性文件中配置,那么使它成为
- 正则表达式大全
yang852220741
html编程正则表达式
今天向大家分享正则表达式大全,它可以大提高你的工作效率
正则表达式也可以被当作是一门语言,当你学习一门新的编程语言的时候,他们是一个小的子语言。初看时觉得它没有任何的意义,但是很多时候,你不得不阅读一些教程,或文章来理解这些简单的描述模式。
一、校验数字的表达式
数字:^[0-9]*$
n位的数字:^\d{n}$
至少n位的数字:^\d{n,}$
m-n位的数字:^\d{m,n}$