自动驾驶仿真:角雷达坐标系转换详解
文章目录
- 一、 为什么要转换角雷达坐标?
- 二、角雷达坐标系和车辆坐标系
-
-
- 1、角雷达的安装角度
- 2、角雷达的坐标系
- 3、车辆坐标系
-
- 三、 坐标系转换思路
-
-
- 1、坐标系绕Z轴旋转
- 2、坐标系平移
- 3、其他目标值转换
-
- 四、 其余角雷达的转换公式
-
-
- 1、左前角雷达转换公式
- 2、左后角雷达转换公式
- 3、右后角雷达转换公式
-
- 五、XY轴旋转拓展
-
-
- 1、旋转公式至矩阵转换
- 2、绕X轴Y轴旋转的矩阵关系式
-
一、 为什么要转换角雷达坐标?
- 我们在做角雷达传感器仿真的时候,使用场景软件搭建角雷达模型会发现角雷达有独立的坐标系,它与车辆坐标系是不一致的。而实际车辆需要用到的目标数据一般都是参照车辆坐标系输出,为了确保仿真角雷达输出的目标数据与实际雷达一致。我们需要对角雷达输出的数据进行适配,即目标值的旋转和平移,以获取到参考车辆坐标系输出的数据。
注:本文主要介绍的是角雷达安装绕Z轴旋转的转换方法,但会提供绕X轴、Y轴旋转的公式。
二、角雷达坐标系和车辆坐标系
1、角雷达的安装角度
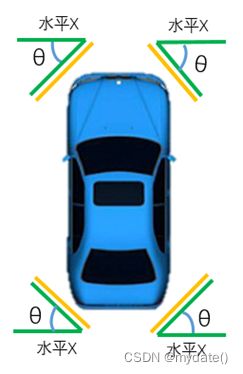
1)如下图所示θ角为角雷达的安装角度(我们的角雷达只绕Z轴旋转),另外需要注意每个车厂对于安装角度的定义不太一致,我们在套用公式的时候需要注意对安装角度的转换。
2、角雷达的坐标系
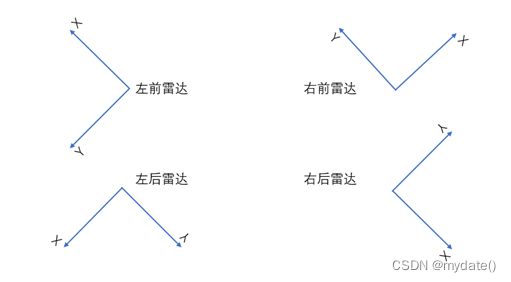
1)如上图角雷达的安装角度所示,橙色的线相当于角雷达的背板,垂直于背板就是角雷达X+(上)的方向,平行于背板就是Y+(左),如下图所示:
3、车辆坐标系
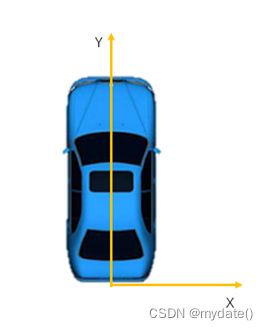
我们要做的就是将角雷达坐标旋转至车辆坐标,但不是真正意义的坐标系旋转,而是角雷达数据的目标值相对于车辆坐标系输出。
三、 坐标系转换思路
1、坐标系绕Z轴旋转
1)使用右前角雷达作为案例进行转换(先旋转再平移),而且为了让公式推导看起来更简单,讲解时先让原点重合一下:
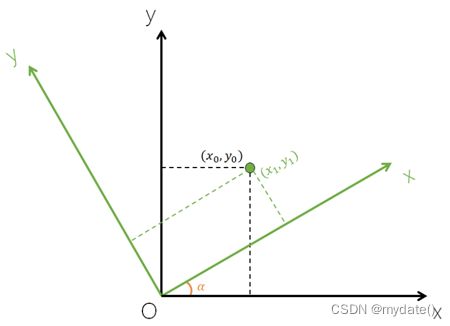
2)下图示,障碍物在右前角雷达的坐标系的坐标为(x1,y1),而目标物在自车坐标系的坐标则为(x0,y0),右角雷达坐标系与自车坐标系的夹角为α,注意α并非右角雷达的安装角度θ。
2)对坐标系做辅助线处理。

由上图得X0(自车坐标系旋转后)公式:
x 0 = x 1 c o s α − y 1 s i n α x_0 = x_1cosα- y_1sinα x0=x1cosα−y1sinα
由上图得Y0(自车坐标系旋转后)公式:
y 0 = x 1 s i n α + y 1 c o s α y_0 = x_1sinα+ y_1cosα y0=x1sinα+y1cosα
注意:
1、以上两条公式是旋转后得原始公式,如果α的参照一致则可以直接代入。
2、由于我的角雷达只是绕Z轴旋转,所以 Z0 = Z1。
并且由于我的α不是实际的车辆安装角度θ,因此:
x 0 = x 1 c o s ( 90 ° − θ ) − y 1 s i n ( 90 ° − θ ) x_0 = x_1cos(90° - θ)- y_1sin(90° - θ) x0=x1cos(90°−θ)−y1sin(90°−θ)
y 0 = x 1 s i n ( 90 ° − θ ) + y 1 c o s ( 90 ° − θ ) y_0 = x_1sin(90° - θ)+ y_1cos(90° - θ) y0=x1sin(90°−θ)+y1cos(90°−θ)
2、坐标系平移
平移只是简单得坐标点平移,假设右角雷达的安装位置为(X2,Y2):
由上图得X0(自车坐标系旋转平移后)公式:
x 0 = x 1 c o s ( 90 ° − θ ) − y 1 s i n ( 90 ° − θ ) + x 2 x_0 = x_1cos(90° - θ)- y_1sin(90° - θ) + x_2 x0=x1cos(90°−θ)−y1sin(90°−θ)+x2
由上图得Y0(自车坐标系旋转平移后)公式:
y 0 = x 1 s i n ( 90 ° − θ ) + y 1 c o s ( 90 ° − θ ) + y 2 y_0 = x_1sin(90° - θ)+ y_1cos(90° - θ)+ y_2 y0=x1sin(90°−θ)+y1cos(90°−θ)+y2
3、其他目标值转换
由于速度加速度等参数是不存其他关系,仅存在三角关系,则它们的关系,例:
v 0 = v 1 c o s ( 90 ° − θ ) 。 v_0 = v_1cos (90°- θ) 。 v0=v1cos(90°−θ)。
四、 其余角雷达的转换公式
已知条件:Z0 = Z1,并且由于角雷达安装在车辆坐标系的位置不同,X2和Y2的方向需要注意(X2,Y2为角雷达在车辆坐标系下的安装位置)
1、左前角雷达转换公式
1)注意左前雷达的X2为负值,Y2为正值:
x 0 = x 1 c o s ( 90 ° + θ ) − y 1 s i n ( 90 ° + θ ) + x 2 x_0 = x_1cos(90° + θ)- y_1sin(90° + θ) + x_2 x0=x1cos(90°+θ)−y1sin(90°+θ)+x2
y 0 = x 1 s i n ( 90 ° + θ ) + y 1 c o s ( 90 ° + θ ) + y 2 y_0 = x_1sin(90° + θ)+ y_1cos(90° + θ)+ y_2 y0=x1sin(90°+θ)+y1cos(90°+θ)+y2
2、左后角雷达转换公式
1)注意左后角雷达的X2为负值,Y2为正值:
x 0 = x 1 c o s ( 270 ° − θ ) − y 1 s i n ( 270 ° − θ ) + x 2 x_0 = x_1cos(270° - θ)- y_1sin(270° - θ) + x_2 x0=x1cos(270°−θ)−y1sin(270°−θ)+x2
y 0 = x 1 s i n ( 270 ° − θ ) + y 1 c o s ( 270 ° − θ ) + y 2 y_0 = x_1sin(270° - θ)+ y_1cos(270° - θ)+ y_2 y0=x1sin(270°−θ)+y1cos(270°−θ)+y2
3、右后角雷达转换公式
1)注意右后角雷达的X2为正值,Y2为正值:
x 0 = x 1 c o s ( 270 ° + θ ) − y 1 s i n ( 270 ° + θ ) + x 2 x_0 = x_1cos(270° + θ)- y_1sin(270° + θ) + x_2 x0=x1cos(270°+θ)−y1sin(270°+θ)+x2
y 0 = x 1 s i n ( 270 ° + θ ) + y 1 c o s ( 270 ° + θ ) + y 2 y_0 = x_1sin(270° + θ)+ y_1cos(270° + θ)+ y_2 y0=x1sin(270°+θ)+y1cos(270°+θ)+y2
五、XY轴旋转拓展
1、旋转公式至矩阵转换
绕Z轴旋转的原始等式:
x 0 = x 1 c o s α − y 1 s i n α y 0 = x 1 s i n α + y 1 c o s α z 0 = z 1 \begin{matrix} x_0 = x_1cosα- y_1sinα \\ y_0 = x_1sinα+ y_1cosα \\ z_0 = z_1 \\ \end{matrix} x0=x1cosα−y1sinαy0=x1sinα+y1cosαz0=z1
将上述等式转换成矩阵,即可得到
[ x 0 y 0 z 0 ] = [ c o s α − s i n α 0 s i n α c o s α 0 0 0 1 ] ∗ [ x 1 y 1 z 1 ] = R Z ∗ [ x 1 y 1 z 1 ] \left[ \begin{array}{c} x_0\\ y_0\\ z_0\\ \end{array} \right] =\left[ \begin{array}{ccc} cosα &-sinα &0\\ sinα &cosα &0\\ 0 &0 &1\\ \end{array} \right]* \left[ \begin{array}{c} x_1\\ y_1\\ z_1\\ \end{array} \right] =RZ* \left[ \begin{array}{c} x_1\\ y_1\\ z_1\\ \end{array} \right] ⎣ ⎡x0y0z0⎦ ⎤=⎣ ⎡cosαsinα0−sinαcosα0001⎦ ⎤∗⎣ ⎡x1y1z1⎦ ⎤=RZ∗⎣ ⎡x1y1z1⎦ ⎤
把角雷达探测到的值和上述RZ矩阵进行矩阵乘法运算,就完成绕Z轴的旋转。这个绕Z轴旋转的矩阵称为RZ。
2、绕X轴Y轴旋转的矩阵关系式
另外只要继续完成了绕X轴和Y轴的旋转(矩阵分别为RX和RY),就是正真意义的完成转换,是否需要绕这两轴旋转的要根据具体情况选择。
RX矩阵:
R X = [ 1 0 0 0 c o s α s i n α 0 − s i n α c o s α ] RX= \left[ \begin{array}{ccc} 1 &0 &0\\ 0 &cosα &sinα\\ 0 &-sinα &cosα\\ \end{array} \right] RX=⎣ ⎡1000cosα−sinα0sinαcosα⎦ ⎤
RY矩阵:
R Y = [ c o s α 0 − s i n α 0 1 0 s i n α 0 c o s α ] RY= \left[ \begin{array}{ccc} cosα &0 &-sinα\\ 0 &1 &0\\ sinα &0 &cosα\\ \end{array} \right] RY=⎣ ⎡cosα0sinα010−sinα0cosα⎦ ⎤
RZ矩阵:
R Z = [ c o s α − s i n α 0 s i n α c o s α 0 0 0 1 ] RZ= \left[ \begin{array}{ccc} cosα &-sinα &0\\ sinα &cosα &0\\ 0 &0 &1\\ \end{array} \right] RZ=⎣ ⎡cosαsinα0−sinαcosα0001⎦ ⎤
绕XYZ轴旋转的坐标转换公式:
[ x 0 y 0 z 0 ] = R X ∗ R Y ∗ R Z ∗ [ x 1 y 1 z 1 ] \left[ \begin{array}{c} x_0\\ y_0\\ z_0\\ \end{array} \right] =RX*RY*RZ* \left[ \begin{array}{c} x_1\\ y_1\\ z_1\\ \end{array} \right] ⎣ ⎡x0y0z0⎦ ⎤=RX∗RY∗RZ∗⎣ ⎡x1y1z1⎦ ⎤
最后加上平移矩阵:
[ x 0 y 0 z 0 ] = R X ∗ R Y ∗ R Z ∗ [ x 1 y 1 z 1 ] + T x y z \left[ \begin{array}{c} x_0\\ y_0\\ z_0\\ \end{array} \right] =RX*RY*RZ* \left[ \begin{array}{c} x_1\\ y_1\\ z_1\\ \end{array} \right]+ Txyz ⎣ ⎡x0y0z0⎦ ⎤=RX∗RY∗RZ∗⎣ ⎡x1y1z1⎦ ⎤+Txyz
综上,完成角雷达的坐标系转换