机器学习笔记——正则化（Regularization）

过度拟合(Overfit)

了解正则化之前，先来看看什么是过拟合。
所谓的过拟合，就是说目前的函数表达式能够完全拟合已知的所有的数据点，但是，对于新给出的数据点，却不能给出相对完善的预测。什么意思嘞？看看下面的图片说明：

线性回归(classification Regression)

第一个：欠拟合(Underfit)，没有将数据体现的特征完全的表达出来。另一种说法就是，这种算法具有高偏差（high bais）。偏差这是一个历史遗留叫法，就是说使用的算法好像有一个很强的偏见，这个算法不顾数据或者事实的不符，先入为主的拟合一条直线，导致拟合数据效果很差。
第二个：”刚好合适(just right)“ ”刚好合适“这不是一个专业的叫法加入二次项，这次的拟合效果看起来很棒（确实，体现出的效果也是很棒的）。
第三个：过拟合(Overfit)，这里适用四阶多项式(four order degree polynomial)，完全照顾所有的已知特征点，但是在数据拟合的过程中，这条多项式曲线不停的上下波动，所以我们认为这个拟合效果不太符合用于做预测。我们称这种情况为：过拟合。另一种叫法称之为：高方差(high variance)。高方差，也是一个历史叫法，如果我们拟合一个高阶多项式，这个假设函数(hypothesis)可以拟合几乎所有的数据，这就面临可能的函数太过庞大，变量太多的问题，我们没有足够的数据约束它，来获得一个好的假设函数。这就是过度拟合。Overfitting

逻辑回归(Logistic Regression)

这里的理解结合线性回归的理解，也是分为三种情况。

从这两个例子中可以看到，过拟合的现象在线性回归中出现，在逻辑回归中也会出现。

为什么会出现过拟合现象？

我们从这个例子中来看，右图中是采用高阶多项式拟合数据效果，为什么会出现这个效果？
我们继续看：
右侧图中的数据点也就5个，然而在左侧出现的数据特种却很多，比如x1:房屋面积，x2:房卧室数量，x3:房龄等等，我们这里要考虑的方面（数据特征）太多了，然而却只给了5组参考样本（样本数量）！也就是说，我们所能参考的数据样本数量远低于要考虑的因素。这样：

在拟合的过程中，为了考虑所有的因素，就不得不采用高阶多项式以满足有的特征，如果对所有的高阶项不加越俗，就会造成过拟合问题。

那么，怎么办？

解决方式

减少特征数量

这里有两个方式：
（1）手动选择保留或者丢弃某些特征；
（2）采用模型选择算法

正则化

今天的主角：正则化。

正则化里保留了所有高阶项，但是减少了高阶项在函数表征过程中的比重，这样，当我们有很多特征需要考虑的时候，通过正则化，就可以保留每一个特征对预测的贡献度而不会产生过度拟合的情况。

为什么这么说？

上图可以看到，左边的是二次项拟合，这个效果"just right",右边的是4阶拟合，就是过拟合，我们左右对比的看一下，直观的看，造成过拟合的情况，就是因为了多了3次项和4次项，如果我们减少这两个高次项的比重，效果会怎么样？
继续看图：

这里，我们改写了Cost function,在后面添加了两项，可以看到，要使代价函数最小化，就要使 θ3 和θ4
尽量的小，当尽量的减小这两项的值后， 右侧中粉红色的线就是效果，这里可以看到，拟合效果好了很多，这个 曲线因为由三次项和四次项的参与，所以整个曲线不是二次曲线，但是，看起来很像，对么？
这就是正则化带来的效果
另外，看一下这个例子中1000θ3 和 1000θ4，这里其实就是对 θ3 和θ4 有了惩罚的意思了，没你不行，但是按照常规套路思考这两个参数，也不行，那就给这两参数一点惩罚吧，让你俩别太出头，有存在的意义就行了。个人理解

正则化

通过以上的了解，来看看正则化背后的思维：

减少所有的参数的贡献值，这样就会有以下效果：
(1) 简单化假设函数
前面的例子,出现的高阶项（θ3 和θ4），减少他们的值，最后的假设函数就会变得相对简单，得到的曲线也就更加平滑。
(2)减少过拟合的趋向

如何选择参数

这个问题确实有难度，比如前面的房价预测的问题：

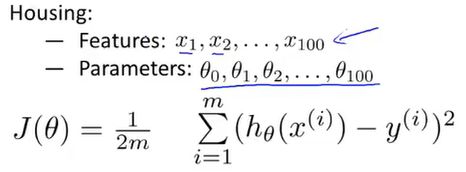
这里我有100个特征需要考虑（面积、卧室数量、花园数量、房龄等等），但是我只有101个数据样本（θ），图片下方就是之前的线性回归的成本函数，这里如何取舍哪些参数留下？那些舍弃呢？亦或者说，哪些参数贡献度高？哪些参数贡献度小？
无从知晓啊，既然无从知晓，那就简单点：对所有的参数都做正则化！

注意正则化参数的选取范围。来看看规范的写法：

来看一下分析：
表达式方括号中左侧是要训练的样本集，右侧带 λ 的表达式就是正则化项，这个正则化就是用来平衡前面训练样本和防止过拟合趋势的。

图中，不加正则化项的蓝色曲线就是典型的过拟合，加上正则化项的品红色曲线，使得拟合曲线更加平滑和符合预期。这就是我们要的效果。

惩罚参数的选择

惩罚参数的选择不能过大，还是房价的例子，如果依据正则化表达式的写法，给 λ 赋予的惩罚因子过大，会出现什么情况？看看下面的表述：

结果就是，特征向几乎全部为零，拟合函数就是一条平行于横轴的直线！这个嘛，就太失败了不是？

所以，为了确保正则化的效果，我们应该将更多的关注点放到这个 λ 中！

梯度下降法的正则化

先看梯度下降法的成本函数的正则化，这里要注意：正则化是对特征项的惩罚，对没有特征项的 θ0 而言是不需要惩罚的，所以，我们对他们要区分看待。

如图，对特征项的正则化，我们添加了惩罚参数，注意不是 λ ，而是 λ/m。

进一步的整理，可以看到，对偏导数整理后，正则化的的表达式其实是对没有正则化的被减数做了优化：θ(j)=1-α（λ/m）.因为学习率α很小，但是样本数量m却很大，所以，正则化后的θ是比原来减少一点，可以这么考虑，就是1和0.99的变化，虽然很小，但是还是想梯度更小的方向迈进了一步。明白了么？

正规方程的正则化

什么是正规方程？简单看一下：

就是通过矩阵的方式显示所有的可能性，那要对这个矩阵求最小化的，咋整？

先看看结果，就是这个：

要对正规方程做正则化，其实就是对括号里的表达式做变化，如下：

不可逆矩阵的正则化

大致说明一下：
对于m*n的矩阵X，如果m0 ,并对做如图中括号里的处理，这是，结果就是一个可逆的的了。可能有点迷糊
简单一点理解：对于奇异矩阵来说，将其做正则化后得到的矩阵就是非奇异了。

补充一下奇异矩阵的知识，来自百度百科：

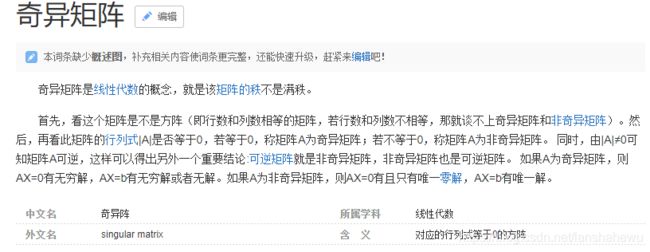
简单说：对于方阵而言，若方阵的行列式值为0，着这个方阵是不可逆的，那么这个仿真就是奇异方阵。对其做正则化后，这个方阵就是可逆的了。

以下这个帮助理解逆矩阵。

逻辑回归函数的正则化

这是之前提到的逻辑回归函数的梯度下降法：

这里在最后添加正则化参数，体会一下：

PS：此学习笔记为学习斯坦福吴恩达机器学习视频笔记。