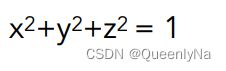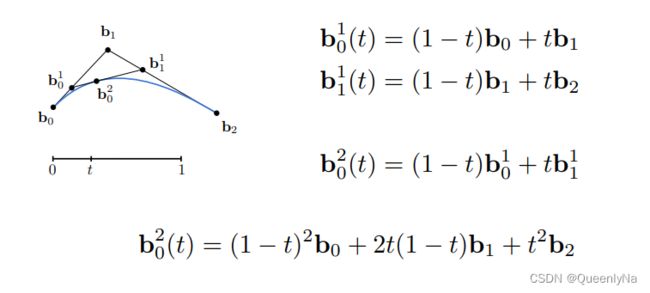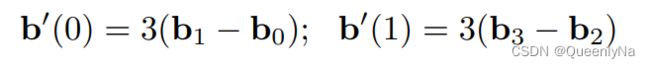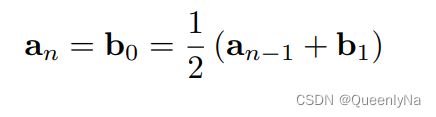图形学 Lecture5 几何 曲线和曲面
几何的不同表示方式:隐式几何 显式几何
曲线和曲面:描述显式几何
隐式几何
>>> 表示一定的关系,不给出实际的点
如球:
- 坏处:很难根据一个函数判断几何形状,即几何都包括哪些点很难,描述一个复杂几何很难,比如奶牛,很难用一个函数去描述。
- 好处:判断一个点是否在这个几何面上,很容易
隐式其他表达方法
-
数学公式(坏处:不直观,不能看出几何形状)
-
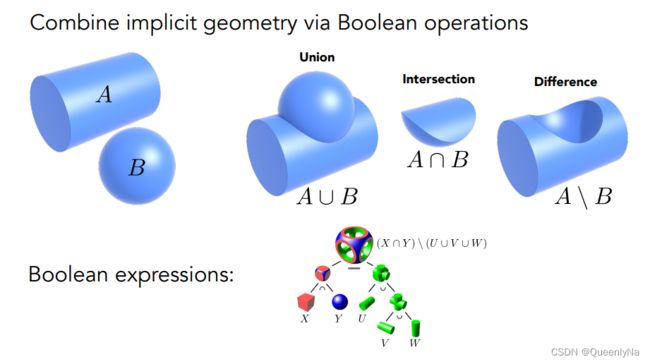
布尔运算
-
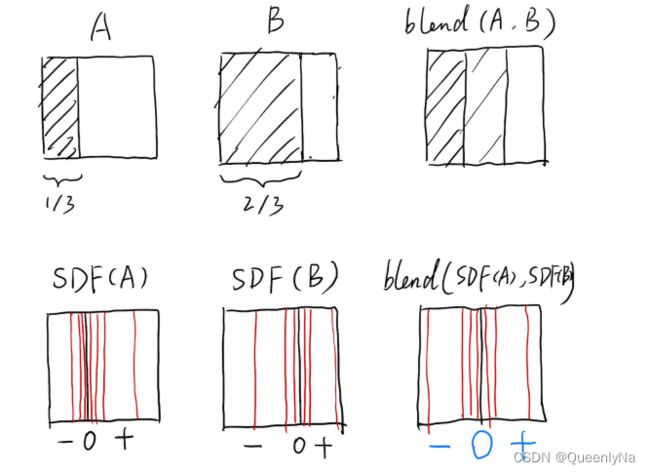
距离函数
几何与几何之间做一个圆滑的过渡,就是靠距离函数的融合。
对于任何一个几何,不直接描述表面,而是描述控件中任何一个点到表面的最近距离。
- 若此空间中的点,在几何外部,则此距离为正;
- 若此空间中的点,在几何内部,则此距离为负。
对距离函数做融合(相加),SDF相加为0的地方,即为融合后的新表面。
SDF是0的地方就是面在的地方。
-
水平集
>>> 想法与距离函数差不多,函数表述在格子上,每个格子上都有值,找到值为0的地方,就可以把整个函数试图描述的物体表面提取出来。
(当然不止可以找等于0的地方)
水平集---纹理
有一个三维纹理描述人体不同位置的密度,从三维信息如何提取物体表面,让密度函数等于某个密度,找到所有这样的位置,就可以找到一个表面。
-
分形
自相似:自己的一个部分和整体长得像
显式几何
显示表示:直接定义几何 或者 通过参数来定义几何
参数定义如下:
也是一种显式表达,因为x y z都给出了对应的公式。
而且,给出任何一个u,v都能找到对应点,就可以画出几何。
- 好处:很容易知道几何形状。
- 坏处:不容易判断点在几何表面上,还是内部,还是外部。
显式几何的其他表示方法
-
点云
不考虑物体是一个表面,而是他表面上的一堆点,点云密度大的时候,就是一个面。
只要点足够密集,就可以构成任何的几何形状。
三维模型扫描之后,也是一堆点。
-
多边形网格
最广泛应用的。
可以用三角形,四边形描述一个物体,但是多边形的连接方法比较复杂,所以这个比点云要复杂。
怎么表示用三角形面形成物体的?
下面一个文件存储一个物体或者一个场景。
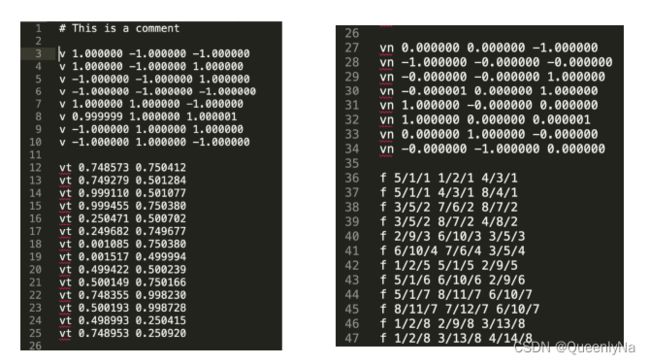
文件名:The Wavefront Object File (.obj) Format
该文件是一个文本文件,就是把顶点 、法线 、纹理坐标分开来表示,再组织起来。
该文件描述的是立方体,左上角表示的是空间中八个点的坐标;
右上角是六种不同的法线,立方体有六个面;
左下角是12个纹理坐标。
右下角是对应关系,以第一行为例:
用第5 1 4个顶点,形成一个三角形,并且这三个顶点,分别用第1 2 3个纹理坐标,并且每个顶点分别用第1 1 1个法线。
定义好多三角形,形成一个网格,构成一个几何物体。
曲线
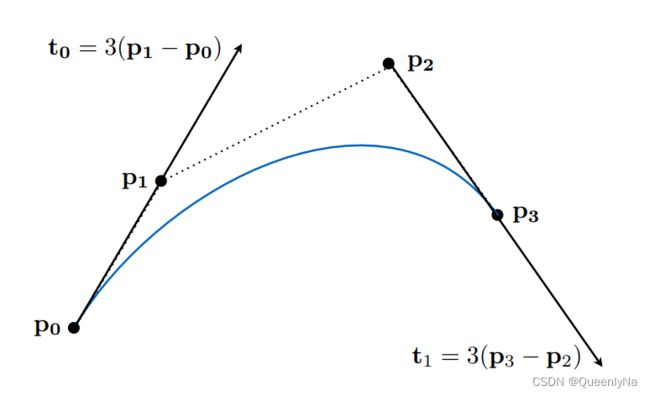
贝塞尔曲线
>>> 用一系列的控制点去定义某一个曲线
- 曲线起始点和终点一定分别在P0和P3上
- 起始和终止的切线一定是P0 P1方向和P2 P3方向
曲线画法
给定控制点,如何去画贝塞尔曲线?
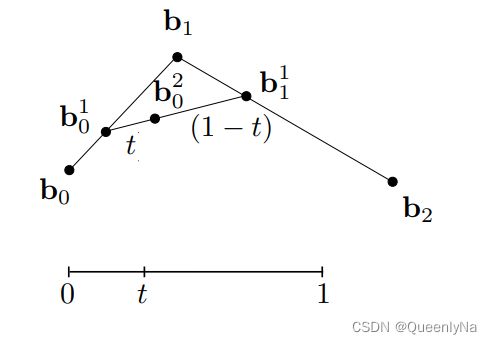
Bézier Curves – de Casteljau Algorithm 算法:
三个控制点---生成二次贝塞尔曲线
最后只有一个点,这个点就是这条贝塞尔曲线在时间 t 所在的位置。
枚举所有的时间 t 就可以把整个曲线画出来。
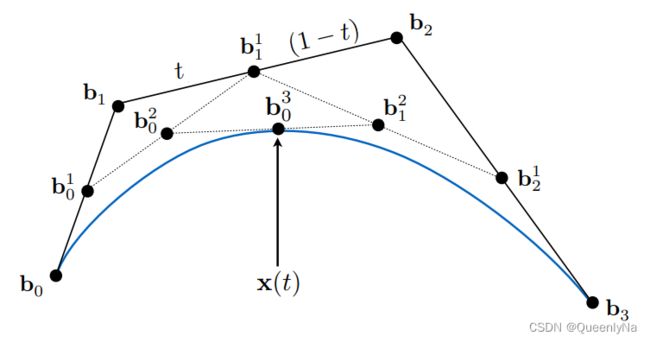
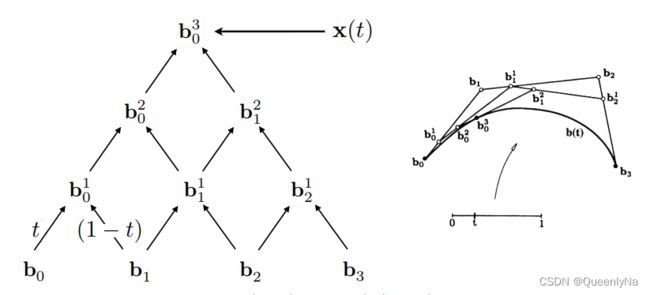
三次贝塞尔曲线也一样:
曲线公式
找参数关系 :贝塞尔曲线上的任意一个点,都是由几个控制点+时间 t 决定。
法一:推导得出
>>> 其实这个式子就是(a+b)的n次方的展开式。
法二:公式计算
计算三次贝塞尔曲线:
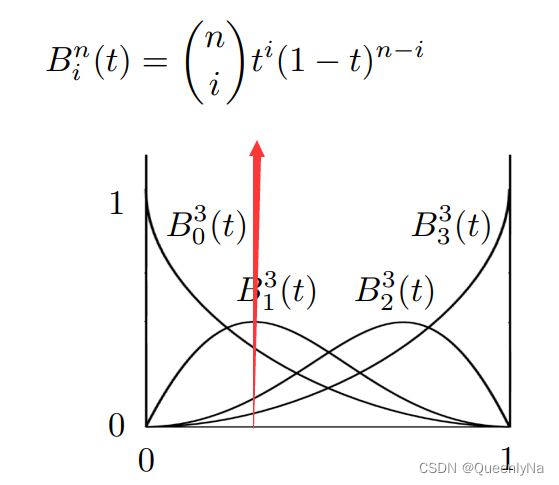
伯恩斯坦多项式的性质:
对于竖直方向上来看,四条曲线的纵坐标加和为1。
贝塞尔曲线的性质
- 在t=0时,在起点;t=1时,在终点。
- 对于三次贝塞尔曲线,规定了起始点和终止点的切线方向。
- 若要对贝塞尔曲线做仿射变换,则可以对控制点做仿射变换,然后重新画就好了。
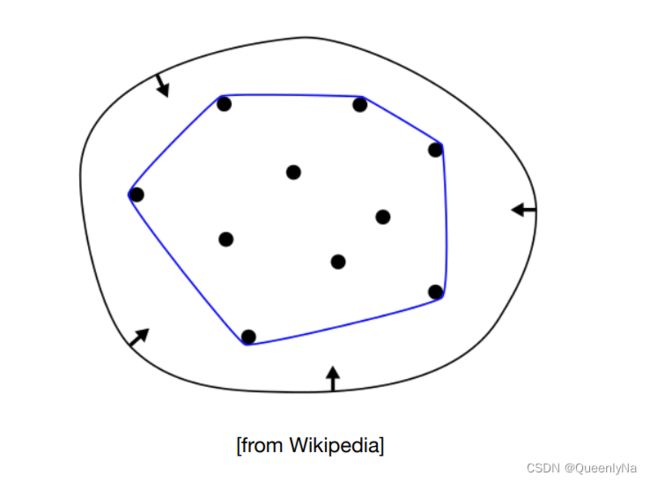
- 凸包性质
>>> 画出来的贝塞尔曲线一定在几个控制点形成的凸包内;
凸包定义类似如下:(一个凸多边形)
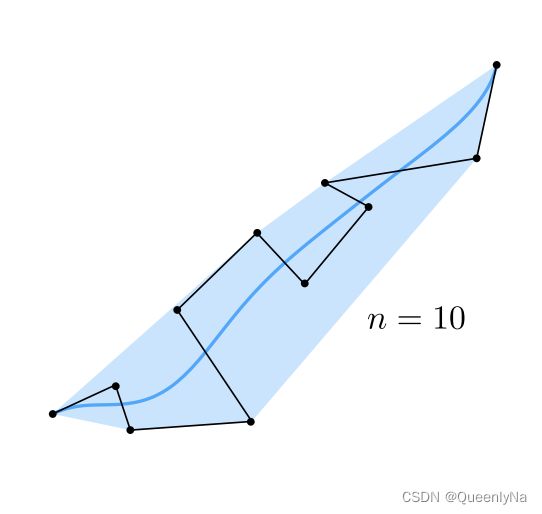
逐段贝塞尔曲线
当控制点多的时候,会不太好控制。
可以每次用很少的控制点 定义一段贝塞尔曲线,然后将贝塞尔曲线相连。
习惯用三次贝塞尔曲线,即每四个控制点定义一条贝塞尔曲线。
怎么保证连起来的贝塞尔曲线是光滑的呢?
>>> 保证导数连续,在方向和大小上(大小相同)
类似于下面这个:
-
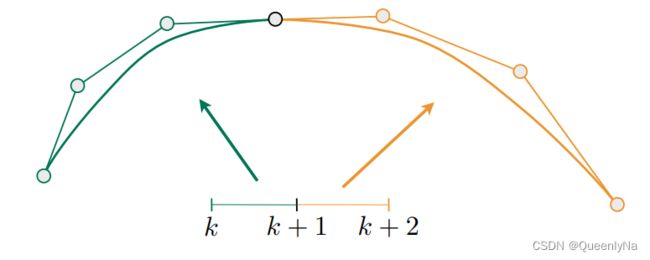
贝塞尔曲线连续性
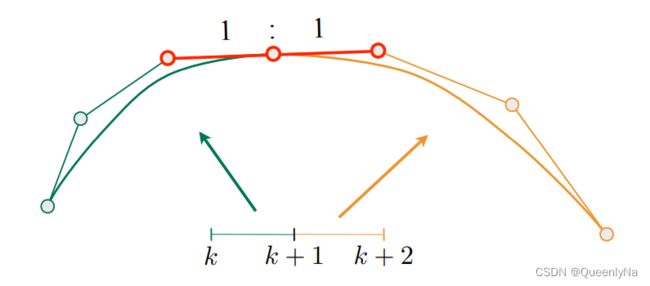
只要第一段的终止点等于等二段的起始点:C0连续。
在一条直线上,且长度相同:C1连续。
其他曲线
Spline曲线(样条曲线)
---一个可控的曲线为样条
B-Spline
>>> 在贝塞尔曲线基础上提出改进,具有局部性,不分段的贝塞尔曲线,有多个控制点时,改变一个控制点,整条曲线都要发生变化,二B-spline曲线,改变一个点,曲线只会发生局部的改变,且不需要分段。(分段的贝塞尔曲线也具有局部性)
曲面
贝塞尔曲面
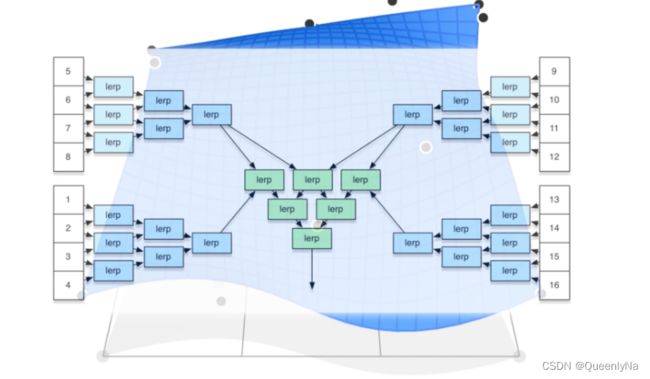
如何用贝塞尔曲线延伸得到贝塞尔曲面?
过程描述:
>>>> 四个控制点分别做贝塞尔曲线,得到的每个 t 时的四个点再当作控制点,生成另一条贝塞尔曲线,就可以了。
在上述过程中,需要两个 t。即需要一个二维的 定义为(u,v)
对于每个时间u,都对任何四个控制点共得到四个点,再给定一个时间v,对形成的四个点找到一个点,那这个点就是曲面在参数(u,v)上面的位置。
>>> 因此,让参数u v都在0 1范围内变化,就可以映射到曲面上任何一个点。
其他曲面
三角形网格
用来表示空间中的集合形状,用的最广泛的一种方法是 网格。
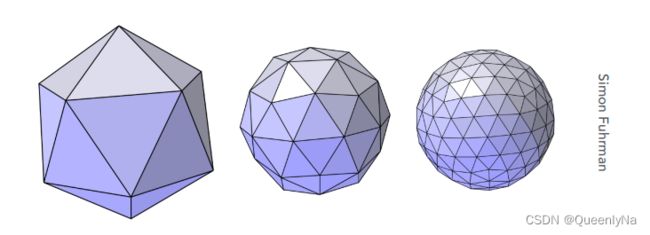
三角形网格为例:
- 网格细分
由第2幅图得到第3幅图。网格更加复杂,得到更光滑曲面。
- 网格简化
网格细分的逆过程。
- 网格正规化
三角形基本都变成和正三角形相似的三角形。
网格曲面操作
-
网格细分
方法一:Loop细分(细分+调整位置)
限制:Loop细分只能用于物体的面都是三角形网格情况。
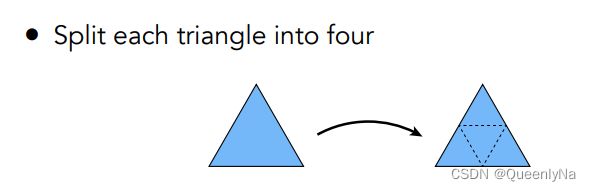
三角形数量增多
按上图方法:将一个三角形拆成四个三角形。
调整三角形位置(调整顶点位置):
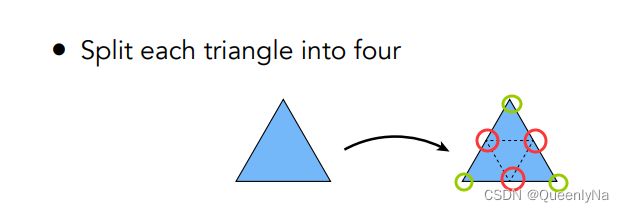
Loop细分中,要找到两种顶点,新的顶点和旧的顶点,分别以不同的规则来改变位置。
如图:红色为新顶点(边的中间),绿色为旧顶点。
- 更改新顶点的位置
找到四个顶点的位置,然后加权平均。
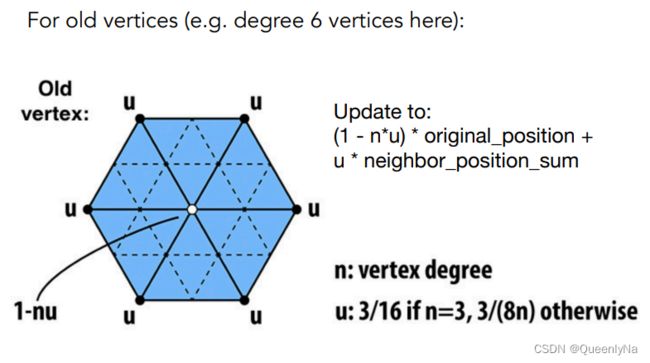
- 更改旧的顶点的位置
旧的顶点的位置更改:由自己 和 临近旧顶点 决定。(n表示本身旧顶点的度)
当n很大时,此旧顶点由自己决定的部分占比重就小了。
细分方法二:Catmull-Clark 细分
若物体不是只有三角形网格的话,即一般情况下,用Catmull-Clark细分
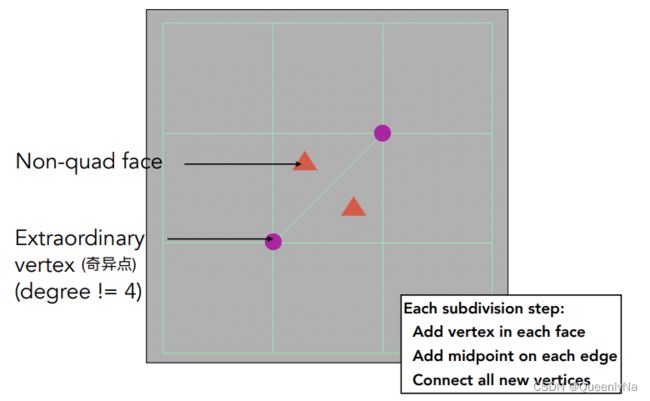
一些概念:四边形面、非四边形面、奇异点(度不为4的点)
>>> 细分做法:每一条边取一个中点,每一个面也取一个中间的点,且边上的中点都连到面上的中间点。
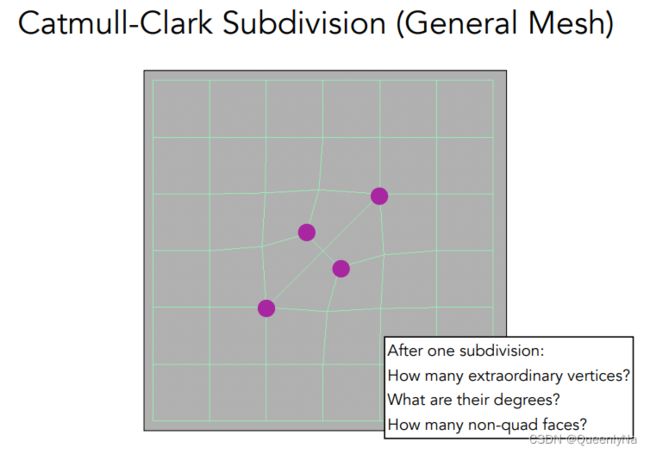
目前有4个奇异点,无四边形面了
Catmull-Clark细分的性质:
在第一次细分之后,增加了非四边形数这么多的奇异点,之后再也不会增加奇异点。
在第一次细分之后,就不会再出现非四边形面了。
>>> 细分过程中,点的位置会发生一系列的变化,再进行细分,再改变点的位置,就会变得越来越光滑。
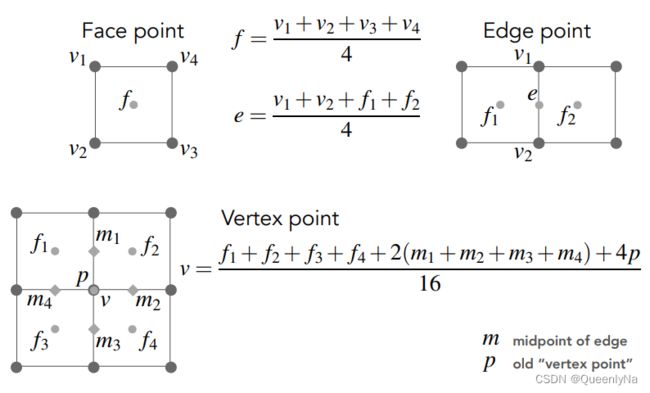
怎么调整点的位置呢?
新的顶点:分为面上的点,边上的点。
旧的顶点:根据相邻的面上的点,边上的点,以及 自己。
-
网格简化
怎样做网格简化?
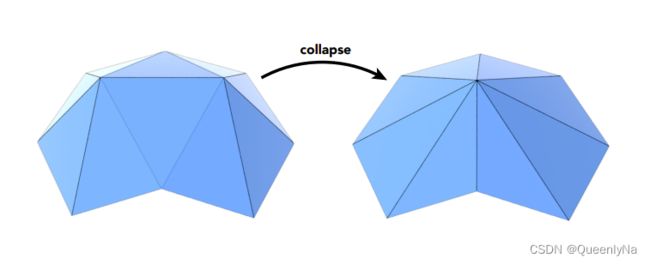
边坍缩(edge collapsing)
要坍缩哪些边呢?
通过 二次误差度量
要将上面三个点用一个点替代:
即找一个点,使得此点到相关面的距离的平方和最小。
通过二次度量误差来确定坍缩哪些边算法:
QEM算法:
每一条边都算一个二次度量误差,然后选值最小的一条边,然后,对这条边所影响的其他边的二次度量误差做更新。