c++ 多重背包状态转移方程_动态规划之背包问题系列
背包问题是一类经典的动态规划问题,它非常灵活,需要仔细琢磨体会,本文先对背包问题的几种常见类型作一个总结,然后再看看LeetCode上几个相关题目。
本文首发于我的博客,传送门
根据维基百科,背包问题(Knapsack problem)是一种组合优化的NP完全(NP-Complete,NPC)问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。NPC问题是没有多项式时间复杂度的解法的,但是利用动态规划,我们可以以伪多项式时间复杂度求解背包问题。一般来讲,背包问题有以下几种分类:
- 01背包问题
- 完全背包问题
- 多重背包问题
此外,还存在一些其他考法,例如恰好装满、求方案总数、求所有的方案等。本文接下来就分别讨论一下这些问题。
1. 01背包
1.1 题目
最基本的背包问题就是01背包问题(01 knapsack problem):一共有N件物品,第i(i从1开始)件物品的重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?
1.2 分析
如果采用暴力穷举的方式,每件物品都存在装入和不装入两种情况,所以总的时间复杂度是O(2^N),这是不可接受的。而使用动态规划可以将复杂度降至O(NW)。我们的目标是书包内物品的总价值,而变量是物品和书包的限重,所以我们可定义状态dp:
dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W那么我们可以将dp[0][0...W]初始化为0,表示将前0个物品(即没有物品)装入书包的最大价值为0。那么当 i > 0 时dp[i][j]有两种情况:
- 不装入第i件物品,即
dp[i−1][j]; - 装入第i件物品(前提是能装下),即
dp[i−1][j−w[i]] + v[i]。
即状态转移方程为
dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]) // j >= w[i]由上述状态转移方程可知,dp[i][j]的值只与dp[i-1][0,...,j-1]有关,所以我们可以采用动态规划常用的方法(滚动数组)对空间进行优化(即去掉dp的第一维)。需要注意的是,为了防止上一层循环的dp[0,...,j-1]被覆盖,循环的时候 j 只能逆向枚举(空间优化前没有这个限制),伪代码为:
// 01背包问题伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必须逆向枚举!!!
dp[j] = max(dp[j], dp[j−w[i]]+v[i])时间复杂度为O(NW), 空间复杂度为O(W)。由于W的值是W的位数的幂,所以这个时间复杂度是伪多项式时间。
动态规划的核心思想避免重复计算在01背包问题中体现得淋漓尽致。第i件物品装入或者不装入而获得的最大价值完全可以由前面i-1件物品的最大价值决定,暴力枚举忽略了这个事实。
2. 完全背包
2.1 题目
完全背包(unbounded knapsack problem)与01背包不同就是每种物品可以有无限多个:一共有N种物品,每种物品有无限多个,第i(i从1开始)种物品的重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?
2.2 分析一
我们的目标和变量和01背包没有区别,所以我们可定义与01背包问题几乎完全相同的状态dp:
dp[i][j]表示将前i种物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W初始状态也是一样的,我们将dp[0][0...W]初始化为0,表示将前0种物品(即没有物品)装入书包的最大价值为0。那么当 i > 0 时dp[i][j]也有两种情况:
- 不装入第i种物品,即
dp[i−1][j],同01背包; - 装入第i种物品,此时和01背包不太一样,因为每种物品有无限个(但注意书包限重是有限的),所以此时不应该转移到
dp[i−1][j−w[i]]而应该转移到dp[i][j−w[i]],即装入第i种商品后还可以再继续装入第种商品。
所以状态转移方程为
dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]]+v[i]) // j >= w[i]这个状态转移方程与01背包问题唯一不同就是max第二项不是dp[i-1]而是dp[i]。
和01背包问题类似,也可进行空间优化,优化后不同点在于这里的 j 只能正向枚举而01背包只能逆向枚举,因为这里的max第二项是dp[i]而01背包是dp[i-1],即这里就是需要覆盖而01背包需要避免覆盖。所以伪代码如下:
// 完全背包问题思路一伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = w[i],...,W // 必须正向枚举!!!
dp[j] = max(dp[j], dp[j−w[i]]+v[i])由上述伪代码看出,01背包和完全背包问题此解法的空间优化版解法唯一不同就是前者的 j 只能逆向枚举而后者的 j 只能正向枚举,这是由二者的状态转移方程决定的。此解法时间复杂度为O(NW), 空间复杂度为O(W)。
2.3 分析二
除了分析一的思路外,完全背包还有一种常见的思路,但是复杂度高一些。我们从装入第 i 种物品多少件出发,01背包只有两种情况即取0件和取1件,而这里是取0件、1件、2件...直到超过限重(k > j/w[i]),所以状态转移方程为:
# k为装入第i种物品的件数, k <= j/w[i]
dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k}同理也可以进行空间优化,需要注意的是,这里max里面是dp[i-1],和01背包一样,所以 j 必须逆向枚举,优化后伪代码为
// 完全背包问题思路二伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必须逆向枚举!!!
for k = [0, 1,..., j/w[i]]
dp[j] = max(dp[j], dp[j−k*w[i]]+k*v[i])相比于分析一,此种方法不是在O(1)时间求得dp[i][j],所以总的时间复杂度就比分析一大些了,为
2.4 分析三、转换成01背包
01背包问题是最基本的背包问题,我们可以考虑把完全背包问题转化为01背包问题来解:将一种物品转换成若干件只能装入0件或者1件的01背包中的物品。
最简单的想法是,考虑到第 i 种物品最多装入 W/w[i] 件,于是可以把第 i 种物品转化为 W/w[i] 件费用及价值均不变的物品,然后求解这个01背包问题。
更高效的转化方法是采用二进制的思想:把第 i 种物品拆成重量为
3. 多重背包
3.1 题目
多重背包(bounded knapsack problem)与前面不同就是每种物品是有限个:一共有N种物品,第i(i从1开始)种物品的数量为n[i],重量为w[i],价值为v[i]。在总重量不超过背包承载上限W的情况下,能够装入背包的最大价值是多少?
3.2 分析一
此时的分析和完全背包的分析二差不多,也是从装入第 i 种物品多少件出发:装入第i种物品0件、1件、...n[i]件(还要满足不超过限重)。所以状态方程为:
# k为装入第i种物品的件数, k <= min(n[i], j/w[i])
dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k}同理也可以进行空间优化,而且 j 也必须逆向枚举,优化后伪代码为
// 完全背包问题思路二伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
for j = W,...,w[i] // 必须逆向枚举!!!
for k = [0, 1,..., min(n[i], j/w[i])]
dp[j] = max(dp[j], dp[j−k*w[i]]+k*v[i])总的时间复杂度约为
3.3 分析二、转换成01背包
采用2.4节类似的思路可以将多重背包转换成01背包问题,采用二进制思路将第 i 种物品分成了
4. 其他情形
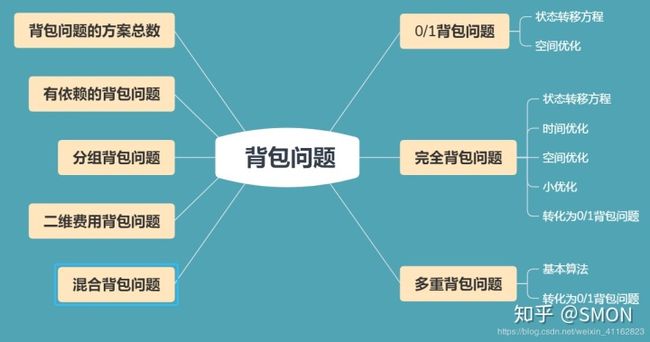
除了上述三种基本的背包问题外,还有一些其他的变种,如下图所示(图片来源)。
本节列举几种比较常见的。
4.1 恰好装满
背包问题有时候还有一个限制就是必须恰好装满背包,此时基本思路没有区别,只是在初始化的时候有所不同。
如果没有恰好装满背包的限制,我们将dp全部初始化成0就可以了。因为任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了。如果有恰好装满的限制,那只应该将dp[0,...,N][0]初始为0,其它dp值均初始化为-inf,因为此时只有容量为0的背包可以在什么也不装情况下被“恰好装满”,其它容量的背包初始均没有合法的解,应该被初始化为-inf。
4.2 求方案总数
除了在给定每个物品的价值后求可得到的最大价值外,还有一类问题是问装满背包或将背包装至某一指定容量的方案总数。对于这类问题,需要将状态转移方程中的 max 改成 sum ,大体思路是不变的。例如若每件物品均是完全背包中的物品,转移方程即为
dp[i][j] = sum(dp[i−1][j], dp[i][j−w[i]]) // j >= w[i]4.3 二维背包
前面讨论的背包容量都是一个量:重量。二维背包问题是指每个背包有两个限制条件(比如重量和体积限制),选择物品必须要满足这两个条件。此类问题的解法和一维背包问题不同就是dp数组要多开一维,其他和一维背包完全一样,例如5.4节。
4.4 求最优方案
一般而言,背包问题是要求一个最优值,如果要求输出这个最优值的方案,可以参照一般动态规划问题输出方案的方法:记录下每个状态的最优值是由哪一个策略推出来的,这样便可根据这条策略找到上一个状态,从上一个状态接着向前推即可。
以01背包为例,我们可以再用一个数组G[i][j]来记录方案,设 G[i][j] = 0表示计算 dp[i][j] 的值时是采用了max中的前一项(也即dp[i−1][j]),G[i][j] = 1 表示采用了方程的后一项。即分别表示了两种策略: 未装入第 i 个物品及装了第 i 个物品。其实我们也可以直接从求好的dp[i][j]反推方案:若 dp[i][j] = dp[i−1][j] 说明未选第i个物品,反之说明选了。
5. LeetCode相关题目
本节对LeetCode上面的背包问题进行讨论。
5.1 Partition Equal Subset Sum(分割等和子集)
Loading...leetcode.com题目给定一个只包含正整数的非空数组。问是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
由于所有元素的和sum已知,所以两个子集的和都应该是sum/2(所以前提是sum不能是奇数),即题目转换成从这个数组里面选取一些元素使这些元素和为sum/2。如果我们将所有元素的值看做是物品的重量,每件物品价值都为1,所以这就是一个恰好装满的01背包问题。
我们定义空间优化后的状态数组dp,由于是恰好装满,所以应该将dp[0]初始化为0而将其他全部初始化为INT_MIN,然后按照类似1.2节的伪代码更新dp:
int capacity = sum / 2;
vectordp(capacity + 1, INT_MIN);
dp[0] = 0;
for(int i = 1; i <= n; i++)
for(int j = capacity; j >= nums[i-1]; j--)
dp[j] = max(dp[j], 1 + dp[j - nums[i-1]]);
更新完毕后,如果dp[sum/2]大于0说明满足题意。
由于此题最后求的是能不能进行划分,所以dp的每个元素定义成bool型就可以了,然后将dp[0]初始为true其他初始化为false,而转移方程就应该是用或操作而不是max操作。完整代码如下:
bool canPartition(vector& nums) {
int sum = 0, n = nums.size();
for(int &num: nums) sum += num;
if(sum % 2) return false;
int capacity = sum / 2;
vectordp(capacity + 1, false);
dp[0] = true;
for(int i = 1; i <= n; i++)
for(int j = capacity; j >= nums[i-1]; j--)
dp[j] = dp[j] || dp[j - nums[i-1]];
return dp[capacity];
}
另外此题还有一个更巧妙更快的解法,基本思路是用一个bisets来记录所有可能子集的和,详见我的Github。
5.2 Coin Change(零钱兑换)
Loading...leetcode.com题目给定一个价值amount和一些面值,假设每个面值的硬币数都是无限的,问我们最少能用几个硬币组成给定的价值。
如果我们将面值看作是物品,面值金额看成是物品的重量,每件物品的价值均为1,这样此题就是是一个恰好装满的完全背包问题了。不过这里不是求最多装入多少物品而是求最少,我们只需要将2.2节的转态转移方程中的max改成min即可,又由于是恰好装满,所以除了dp[0],其他都应初始化为INT_MAX。完整代码如下:
int coinChange(vector& coins, int amount) {
vectordp(amount + 1, INT_MAX);
dp[0] = 0;
for(int i = 1; i <= coins.size(); i++)
for(int j = coins[i-1]; j <= amount; j++){
// 下行代码会在 1+INT_MAX 时溢出
// dp[j] = min(dp[j], 1 + dp[j - coins[i-1]]);
if(dp[j] - 1 > dp[j - coins[i-1]])
dp[j] = 1 + dp[j - coins[i-1]];
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
注意上面1 + dp[j - coins[i-1]]会存在溢出的风险,所以我们换了个写法。
另外此题还可以进行搜索所有可能然后保持一个全局的结果res,但是直接搜索会超时,所以需要进行精心剪枝,剪枝后可击败99%。详见我的Github。
5.3 Target Sum(目标和)
Loading...leetcode.com这道题给了我们一个数组(元素非负),和一个目标值,要求给数组中每个数字前添加正号或负号所组成的表达式结果与目标值S相等,求有多少种情况。
假设所有元素和为sum,所有添加正号的元素的和为A,所有添加负号的元素和为B,则有sum = A + B 且 S = A - B,解方程得A = (sum + S)/2。即题目转换成:从数组中选取一些元素使和恰好为(sum + S) / 2。可见这是一个恰好装满的01背包问题,要求所有方案数,将1.2节状态转移方程中的max改成求和即可。需要注意的是,虽然这里是恰好装满,但是dp初始值不应该是inf,因为这里求的不是总价值而是方案数,应该全部初始为0(除了dp[0]初始化为1)。所以代码如下:
int findTargetSumWays(vector& nums, int S) {
int sum = 0;
// for(int &num: nums) sum += num;
sum = accumulate(nums.begin(), nums.end(), 0);
if(S > sum || sum < -S) return 0; // 肯定不行
if((S + sum) & 1) return 0; // 奇数
int target = (S + sum) >> 1;
vectordp(target + 1, 0);
dp[0] = 1;
for(int i = 1; i <= nums.size(); i++)
for(int j = target; j >= nums[i-1]; j--)
dp[j] = dp[j] + dp[j - nums[i-1]];
return dp[target];
}
5.4 Ones and Zeros(一和零)
Loading...leetcode.com题目给定一个仅包含 0 和 1 字符串的数组。任务是从数组中选取尽可能多的字符串,使这些字符串包含的0和1的数目分别不超过m和n。
我们把每个字符串看做是一件物品,把字符串中0的数目和1的数目看做是两种“重量”,所以就变成了一个二维01背包问题,书包的两个限重分别是 m 和 n,要求书包能装下的物品的最大数目(也相当于价值最大,设每个物品价值为1)。
我们可以提前把每个字符串的两个“重量” w0和w1算出来用数组存放,但是注意到只需要用一次这两个值,所以我们只需在用到的时候计算w0和w1就行了,这样就不用额外的数组存放。完整代码如下:
int findMaxForm(vector& strs, int m, int n) {
int num = strs.size();
int w0, w1;
vector>dp(m+1, vector(n+1, 0));
for(int i = 1; i <= num; i++){
w0 = 0; w1 = 0;
// 计算第i-1个字符串的两个重量
for(char &c: strs[i - 1]){
if(c == '0') w0 += 1;
else w1 += 1;
}
// 01背包, 逆向迭代更新dp
for(int j = m; j >= w0; j--)
for(int k = n; k >= w1; k--)
dp[j][k] = max(dp[j][k], 1+dp[j-w0][k-w1]);
}
return dp[m][n];
}
6. 总结
本文讨论了几类背包问题及LeetCode相关题目,其中01背包问题和完全背包问题是最常考的,另外还需要注意一些其他变种例如恰好装满、二维背包、求方案总数等等。除了本文讨论的这些背包问题之外,还存在一些其他的变种,但只要深刻领会本文所列的背包问题的思路和状态转移方程,遇到其它的变形问题,应该也不难想出算法。如果想更加详细地理解背包问题,推荐阅读经典的背包问题九讲。
参考
- 背包问题 - 维基百科
- 背包问题-笔记整理
- 动态规划与贪婪法题16:背包问题总结 - CSDN
- 背包问题九讲2.0 - 崔添翼
更多我的LeetCode中文题解,可前往GitHub查看:https://github.com/ShusenTang/LeetCode