kaldi单音素模型训练 - train_mono.sh脚本解读
提示:本文适合kaldi的初学者,但最好有过运行kaldi的经验,并且大概了解EM算法。本文比较细致地对train_mono.sh脚本进行了解读,包括其源码,输入输出,以及对输出文件的内容都有详细的解释,可能会有点琐碎,但个人认为对理解kaldi中声学模型的训练会有一定的帮助。
文章目录
- 前言
- 一、train_mono.sh的输入和输出
- 二、特征读取
- 三、模型初始化
- 四、参数迭代更新
-
- 1. 对齐
-
- 1-1 文本状态图
- 1-2 强制对齐
- 2. GMM模型迭代
- 总结
前言
上下文无关的单音素模型,或者monophone模型,是声学模型中最基础的模型。用HMM建模时每个状态对应一个上下文无关的单音素,大多数kaldi的训练脚本run.sh都是从monophone模型的训练开始,重复几次训练-对齐的过程,用最后HMM-GMM模型的对齐结果作为label去训练DNN模型。
本文着重讲解一下steps/train_mono.sh脚本,分析单音子模型的生成过程,之后上下文相关三音素模型的训练过程和这个大致上是一样的,所以理解最基础的模型非常重要。
一、train_mono.sh的输入和输出
在run.sh中该脚本是这样调用的
steps/train_mono.sh --boost-silence 1.25 --nj $n --cmd "$train_cmd" data/mfcc/train data/lang exp/mono
脚本使用说明如下:
steps/train_mono.sh
Usage: steps/train_mono.sh [options] <data-dir> <lang-dir> <exp-dir>
e.g.: steps/train_mono.sh data/train.1k data/lang exp/mono
main options (for others, see top of script file)
--config <config-file> # config containing options
--nj <nj> # number of parallel jobs
--cmd (utils/run.pl|utils/queue.pl <queue opts>) # how to run jobs.
–boost-slience:
大多数情况下可以保持默认,训练数据中静音数据所占比例不同,在进行对齐时句子头尾静音帧会被句子头尾的非静音模型吃掉(静音过弱),或者相反静音模型吃掉了句子头尾的一些语音帧(静音过强)。在这种情况下我们可以为静音模型加入一个可人工调节的系数对静音模型的打分进行调节。
–nj:
kaldi脚本中常用的多线程控制参数,kaldi会把程序分成nj份并行运行提高效率,计算机性能越好nj可以设置越高。
–cmd:
可以被设置为run.pl或者queue.pl,utils/run.sh这个perl脚本的作用是多任务的执行某个程序,可以独立于kaldi之外运行,比如:
perl utils/run.sh JOB=1:8 log.JOB.txt echo "This is the job JOB"
就是将echo命令执行了8次,对于比较大的训练数据将程序分成多分执行会提高效率。
data-dir:训练数据特征矩阵的保存目录
lang-dir:保存了音素集和其对应的序号,具体来说monophone模型的训练需要用到phones.txt这个文件
exp-dir:输出模型的保存路径,除了模型还会保存一些日志和对齐文件。
二、特征读取
train_mono.sh 脚本中读取并保存特征的核心代码是
feats="ark,s,cs:apply-cmvn $cmvn_opts --utt2spk=ark:$sdata/JOB/utt2spk scp:$sdata/JOB/cmvn.scp scp:$sdata/JOB/feats.scp ark:- | add-deltas $delta_opts ark:- ark:- |"
分析这个指令的同时会讲解一些kaldi的数据读写机制,一般情况下kaldi中的数据会被保存为以scp为后缀的索引数据表,和以ark为后缀的数据内容。scp一般是文本格式可以直接读取,ark一般是二进制格式需要用相应的指令读取,其中ark文件保存了数据核心内容,而scp文件保存了ark文件的路径以及特定数据段的地址偏移量,根据路径可以找到ark文件,根据地址偏移量可以定位到某一数据段。
初学kaldi时看这行指令的话可能会怀疑自己,我就是这么过来的。首先看一下这行代码中包含了两个程序,apply-cmvn和add-deltas, 先不看开头的ark,s,cs,单从linux管道机制来看的话不难理解这行代码,它将apply-cmvn的结果送给add-deltas处理,再送到标准输出保存到feats变量中。
apply-cmvn 的输入输出如下所示:
Usage: apply-cmvn [options] (<cmvn-stats-rspecifier>|<cmvn-stats-rxfilename>) <feats-rspecifier> <feats-wspecifier>
该程序对MFCC特征矩阵进行归一化处理,即将其特征分布转换为标准正态分布,为此需要先计算特征值的均值方差等统计量,这部分会在其他文章中详细讲解。这些统计量保存在 mfcc/ 目录下,例如cmvn_train.ark和cmvn_train.scp, 前面说过scp文件保存数据索引,ark文件保存数据内容,都是成对出现。进一步来说,该程序读取cmvn.scp和feats.scp并输出归一化后的特征值。
$cmvn_opts和 –utt2spk都是该指令 [options] 的一部分, –utt2spk 指定utt2spk文件的路径,ark: 表示要输入的是ark格式文件,至于为什么不直接用 –utt2spk=$sdata/JOB/utt2spk,因为程序源码就是这么设定的,他要读取的是一个respecifier类型的数据,所以必须是kaldi中的ark或者scp,后面的 scp:$sdata/JOB/cmvn.scp也是一样的 scp: 表示要读取scp格式的文件,而最后 ark:- 表示以ark二进制格式对数据进行标准输出,在这里简单演示一下:
首先通过数据索引找到ark文件路径查看一下其内容: mfcc/train/raw_mfcc_train.1.ark (众多utterance中的一条)
copy-feats ark:mfcc/train/raw_mfcc_train.1.ark ark,t:feats.txt
copy-feats 是kaldi中专门用来读取特征的程序,跟前面一样ark: 表示读取ark二进制格式数据内容,ark,t: 表示将输出的ark格式特征数据转换为可读的文本格式,没有t的话就直接输出ark格式。下面读取feats.txt文件:
A02_000 [
54.33462 -22.4812 -5.116314 -5.651031 -3.921801 -3.74971 -0.5585474 -8.126663 -6.963806 -3.532409 -5.939445 9.59717 10.88082
55.02431 -22.74367 -7.128184 -7.080585 -1.124176 -5.744934 -9.088843 -4.740393 -6.350121 -1.8025 -5.514661 6.663599 -2.771008
...
其中一行表示一帧,一帧特征13维
下面对其进行归一化处理并读取处理后的结果:
apply-cmvn --utt2spk=ark:data/mfcc/train/split20/1/utt2spk scp:data/mfcc/train/split20/1/cmvn.scp scp:data/mfcc/train/split20/1/feats.scp ark,t:feats_cmvn.txt
A02_000 [
-24.58855 -15.69923 6.681437 -9.191471 6.299015 6.853975 2.428551 5.737149 -4.460067 3.940732 -3.256021 13.95298 11.6103
-23.89886 -15.9617 4.669566 -10.62103 9.09664 4.858751 -6.101745 9.123419 -3.846382 5.670641 -2.831237 11.01941 -2.041526
...
可以看到归一化之后维度是一样的,而数据分布发生了变化。
之后我们用add-deltas 对特征进行差分处理并查看其输出结果:
add-deltas ark:feats_cmvn.ark ark,t:feats_delta.txt
A02_000 [
-24.58855 -15.69923 6.681437 -9.191471 6.299015 6.853975 2.428551 5.737149 -4.460067 3.940732 -3.256021 13.95298 11.6103 0.2586328 -0.2887155 -0.2956386 0.4189454 0.9884939 -0.4275481 -0.6098861 2.529619 0.33139 1.851123 1.975248 -2.967023 -2.998636 0.08879703 -0.1391298 -0.4438906 0.5 810721 0.2548139 -0.6498731 -0.4282904 0.1762799 0.422885 0.3236066 0.3345177 -0.2845525 0.2698589
-23.89886 -15.9617 4.669566 -10.62103 9.09664 4.858751 -6.101745 9.123419 -3.846382 5.670641 -2.831237 11.01941 -2.041526 0.1982848 -0.4199495 -0.4250319 1.60307 1.451252 -1.767199 -1.894599 1.841557 3.114731 2.303706 1.454887 -2.174996 -1.465199 0.02241445 -0.1562762 -0.5248272 0.5395 913 -0.08801013 -0.4475003 -0.05739291 -0.5786252 0.2447209 -0.5897465 -0.192215 0.2954182 1.11121
可以观察到每一帧的特征维数变成了39维,脚本中的add-deltas $delta_opts ark:- ark:-,里面ark:- ark:- 一个表示标准输入一个表示标准输出,kaldi脚本里面会有很多这样的写法,不熟悉kaldi的IO机制的话很容易混淆。
最后经过归一化和差分处理的特征值被保存到 $feats 变量中。
三、模型初始化
首先在 [stage -le 3] 的部分用 feat-to-dim 检查一下特征值的维数是否正确,下面进行初始化。
$cmd JOB=1 $dir/log/init.log \
gmm-init-mono $shared_phones_opt "--train-feats=$feats subset-feats --n=10 ark:- ark:-|" $lang/topo $feat_dim \
$dir/0.mdl $dir/tree || exit 1;
$cmd 在这里表示 run.pl ,将程序分成多个部分执行,因为是初始化所以将JOB设置为1就足够了,初始化的核心程序是 gmm-init-mono,先看看其输入输出:
Initialize monophone GMM.
Usage: gmm-init-mono <topology-in> <dim> <model-out> <tree-out>
e.g.:
gmm-init-mono topo 39 mono.mdl mono.tree
模型初始化可以不需要训练数据的特征,在这里用 –train-feat 取训练特征的一部分进行初始化有利于后续的训练,简单说一下这里的特征读取机制。subset-feats 复制并返回输入特征的一部分,用参数n来指定,第一个ark:- 表示读取标准输入,即前面的 $feats, 第二个 ark:- | 将结果标准输出送到train-feats中。
gmm-init-mono 读取HMM拓扑结构topo 和特征维数 $feat_dim,输出初始化模型 0.mdl 和初始化决策树 tree,这些文件都可以在exp/mono目录下看到。
首先看下data/lang/topo, 在这里我以 thchs30 数据集为例:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218
0 0 0 0.75 1 0.25
1 1 1 0.75 2 0.25
2 2 2 0.75 3 0.25
3
1
0 0 0 0.25 1 0.25 2 0.25 3 0.25
1 1 1 0.25 2 0.25 3 0.25 4 0.25
2 2 1 0.25 2 0.25 3 0.25 4 0.25
3 3 1 0.25 2 0.25 3 0.25 4 0.25
4 4 4 0.75 5 0.25
5
topo 主要由两部分构成,一部分是发音因素即这里的2-218,每个音素由3状态HMM建模,转移概率被初始化为0.75和0.25,另一部分是静音音素1,由5状态HMM构成。
下面用gmm-copy 看一下初始化的模型 0.mdl:
gmm-copy --binary=false 0.mdl 0.txt
总体来看0.mdl 中由一个
656
1 0 0
1 1 1
1 2 2
1 3 3
1 4 4
2 0 5
2 1 6
2 2 7
3 0 8
3 1 9
3 2 10
以 1 2 2 为例,表示1号音素的2号状态,1是音素序号,2是状态号,第二个2是pdf-id, 1号是静音因素比较特殊所以有5个HMM状态,用01234表示,其他因素只有3个状态,用012表示,简单计算一下就是 1 * 5 + 217 * 3 = 656,所以 pdf-id就是0-655,每个状态对应一个GMM分布,所以用 pdf-id来表示。再往下走是LogProbs
[ 0 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294 -0.2876821 -1.386294
...
这些是取对数之后的转移概率,1320个,结合topo的HMM结构,3状态HMM有6种转移情况,5状态HMM里面有18中转移情况,简单计算一下就是 217 * 6 + 1 * 18 = 1320,有一说一这部分关于模型文件的解读在现有的学习资料中很难找到。到此为止HMM的转移状态部分就结束了,由
下面是GMM部分,每个状态对应一个GMM,由
[ -89.02968 ]
[ 1 ]
[
-0.01003729 -0.0529411 -0.01423996 -0.0006562257 -0.006262357 0.01076035 -0.01492695 0.004069046 -0.003475642 0.004554303 0.006600214 -0.000567495 0.001459192 -9.853709e-05 -0.0004488721 -0.0002991017 -0.0002230214 -0.0002823436 -0.0001968009 -7.354857e-05 -0.0001315833 0.0001223269 -0.0005158153 -4.267746e-05 6.358125e-05 0.0002519431 0.0001443378 0.0001565464 -4.300946e-06 -8.963557e-05 0.0003367846 0.0001465993 0.0001015042 -0.0003141357 0.0001630248 2.556936e-06 -0.0002067688 -0.0001552064 0.0002767602 ]
[
0.004561778 0.00581147 0.005156674 0.00322543 0.003529151 0.004132621 0.006279969 0.005018717 0.006004524 0.005533454 0.006781458 0.005537271 0.008269035 0.1873672 0.1173657 0.1072205 0.0856709 0.06953733 0.083712 0.0906736 0.07965995 0.08121819 0.087541 0.09525643 0.09399333 0.1228067 1.376921 0.7685885 0.6930602 0.5778249 0.4501231 0.4999908 0.4913502 0.451563 0.4362432 0.5041118 0.5247324 0.5248606 0.6666974 ]
到此我们得到了初始化的模型0.mdl, 218个音素,656个状态,每个状态对应一个只包含一个高斯分量的GMM,我们甚至可以直接用这个模型进行语音识别,但效果会很差。后续的参数迭代中我们要更新每个状态的HMM转移概率和GMM的均值向量以及协方差矩阵,同时进行单高斯分量到混合高斯分量的分裂。
四、参数迭代更新
模型初始化之后的两行代码是:
numgauss=`gmm-info --print-args=false $dir/0.mdl | grep gaussians | awk '{print $NF}'`
incguass=$[($totguass-$numgauss)/$max_iter_inc]
numgauss 表示当前模型中高斯分量总数,该信息通过gmm-info 程序读取,totgauss 表示最后的模型中高斯分量总数,这是提前设定好的,incgauss 表示每次迭代中增加多少个高斯分量。totgauss一般默认为1000,同时总迭代次数 num_iters被设置为40。
经典HMM理论中训练GMM-HMM模型需要Baum-Welch算法,不需要知道训练样本每一帧对应哪个状态,只需给出训练样本序列就可以根据EM算法求取各参数在整个序列上的最大似然估计。Kaldi中使用维特比训练,稍有不同,也使用EM,但需要提前知道每一帧的状态,该算法速度更快,且性能与Baum-Welch算法相近。
1. 对齐
1-1 文本状态图
首先需要考虑的问题就是如何获取每一帧对应的状态,或者状态号作为训练标签,注意这里不像普通的机器学习同时给你训练数据和标签,手动对每一帧的状态进行标注几乎是不可能的,虽然语音有对应的文本数据,但这些文本无法直接对应到每一帧上,因此我们需要对训练序列进行对齐处理,也就是文献中经常出现的alignment。
在stage=-2阶段,构建了一个直线型状态图,其内容包含训练句子的标注文本所对应的状态:
if [ $stage -le -2 ]; then
echo "$0: Compiling training graphs"
$cmd JOB=1:$nj $dir/log/compile_graphs.JOB.log \
compile-train-graphs --read-disambig-syms=$lang/phones/disambig.int $dir/tree $dir/0.mdl $lang/L.fst \
"ark:sym2int.pl --map-oov $oov_sym -f 2- $lang/words.txt < $sdata/JOB/text|" \
"ark:|gzip -c >$dir/fsts.JOB.gz" || exit 1;
fi
其对应的文件是一系列fsts.*.gz 的压缩文件,每个压缩文件对应一部分标注文本的状态图,我们取其中一段文本进行观察,首先在mono目录下单独执行构建图的指令:
compile-train-graphs --read-disambig-syms=../../data/lang/phones/disambig.int tree 0.mdl ../../data/lang/L.fst "ark:../../utils/sym2int.pl --map-oov $oov_sym -f 2- ../../data/lang/words.txt < ../../data/mfcc/train/split20/1/text|" ark:example.fst
我们可以看到生成的example.fst的文件,需要注意的是,这不是一个标准的fst格式文件,用fstprint去打印的话会提示文件头无法识别,可能是因为里面包含文本id,如A02之类的,但我把他们删了也不行。总之想看到pdf格式的WFST状态图的话必须先把他转换为fst格式文件,这里我用了一个很僵硬的办法,就是 非标准fst文件→文本格式→标准fst文件。
具体做法就是在刚才的指令最后加上ark,t:example.fst.txt ,这是之前讲过的将ark格式文件转换为文本文件输出的方法,我们得到example.fst.txt, 打开这个文件发现它由多个文本段落组成,我们只保留第一个A02_000(如果是其他数据集的话会有不同的标识方法),删掉其他的段落,最后再把A02_000删除,使其成为一个可以被识别的fst文本,执行fst编译程序(把前面的example.fst覆盖了也没事):
fstcompile example.fst.txt example.fst
这里得到的example.fst是标准格式的fst文件,可以通过fstprint 读取,最后我们用fstdraw来绘制pdf格式的WFST状态图:
stdraw --isymbols=transition-dict.txt example.fst | dot -Tps | ps2pdf - example.pdf
在看状态图之前先给出标注文本:
A02_000 绿 是 阳春 烟 景 大块 文章 的 底色 四月 的 林 峦 更是 绿 得 鲜活 秀媚 诗意 盎然
整体来看这个状态图是一个直线型的图,包含了标注文本的状态序列,同时每个状态有指向自身的跳转即self-loop
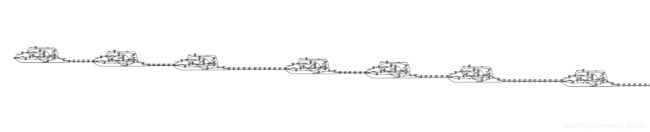
将其开头部分放大来看的话,可以发现他是 “绿(lv4)” 音素状态序列, l的3个状态和v4的3个状态,后面紧跟着 “是(sh ix4)” 和 “阳春(ii ang2 ch un1)” 等等。
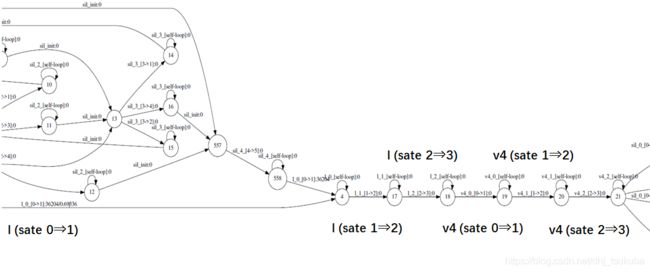
1-2 强制对齐
我们需要根据语音帧和已有的声学模型(0.mdl)选取状态图中的一条最优路径,(由于self-loop的存在,实际上上面的状态图中有无数条路径,比如你可以永远停在某个状态直到结束)把各帧匹配到状态图上,这样就可以得到每一帧所对应的状态。其实这样做下来,就是一个完整的语音识别解码过程,只不过就是你只能在这个直线型的状态图中解码。我们还是以上面的文本为例进行说明,脚本中执行的代码是:
if [ $stage -le -1 ]; then
echo "$0: Aligning data equally (pass 0)"
$cmd JOB=1:$nj $dir/log/align.0.JOB.log \
align-equal-compiled "ark:gunzip -c $dir/fsts.JOB.gz|" "$feats" ark,t:- \| \
gmm-acc-stats-ali --binary=true $dir/0.mdl "$feats" ark:- \
$dir/0.JOB.acc || exit 1;
fi
我们同样在终端单独执行查看输出结果,注意这里的example_feats.scp和example_cmvn.scp都是从data/mfcc/train/spli20/1/feats.scp cmvn.scp复制过来的,训练数据的一部分,其他数据集有相似的目录结构。注意这里的example.fst需要用前面的compile-train-graphs重新生成一下,因为align-equal-compile的输入参数并不是标准的fst格式文件,所以直接用刚才的example.fst会报错。
sdata=../../data/mfcc/train/split20
feats="ark,s,cs:apply-cmvn --utt2spk=ark:$sdata/1/utt2spk scp:example_cmvn.scp scp:example_feats.scp ark:- | add-deltas ark:- ark:- |"
align-equal-compiled ark:example.fst "$feats" ark,t:example_align.txt
结果保存在example_align.txt中:
A02_000 4 1 1 1 13 15 15 15 6 5 5 5 12 10 10 10 18 17 17 17 758 757 757 757 760 759 759 759 762 761 761 761 1196 1195 1195 1195 1198 1197 1197 1197 1200 1199 1199 1199 4 1 1 1 16 15 15 15 18 17 17 17 896 895 895 895 898 897 897 897 900 899 899 899 692 691 691 691 694 693 693 693 696 695 695 695 548 547 547 547 550 549 549 549 552 551 551 551 464 463 463 463 466 465 465 465 468 467 467 467 188 187 187 187 190 189 189 189 192 191 191 191 1112 1111 1111 1111 1114 1113 1113 1113 1116 1115 1115 1115 2 1 1 1 7 5 5 5 14 15 15 15 12 10 10 10 18 17 17 17 548 547 547 547 550 549 549 549 552 551 551 551 428 427 427 427 430 429 429 429 432 431 431 431 3 1 1 1 12 10 10 10 18 17 17 17 746 745 745 745 748 747 747 747 750 749 749 749 596 595 595 595 598 597 597 597 600 599 599 599 4 1 1 1 13 15 15 15 7 5 5 5 16 15 15 15 18 17 17 17 194 193 193 193 196 195 195 195 198 197 197 197 38 37 37 37 40 39 39 39 42 41 41 41 752 751 751 751 754 753 753 753 756 755 755 755 986 985 985 985 988 987 987 987 990 989 989 989 1172 1171 1171 1171 1174 1173 1173 1173 1176 1175 1175 1175 1118 1117 1117 1117 1120 1119 1119 1119 1122 1121 1121 1121 1316 1315 1315 1315 1318 1317 1317 1317 1320 1319 1319 1319 116 115 115 115 118 117 117 117 120 119 119 119 2 1 1 1 6 5 5 5 9 10 10 10 8 5 5 5 18 17 17 17 194 193 193 193 196 195 195 195 198 197 197 197 374 373 373 373 376 375 375 375 378 377 377 377 2 1 1 1 7 5 5 5 16 15 15 15 18 17 17 17 194 193 193 193 196 195 195 195 198 197 197 197 380 379 379 379 382 381 381 381 384 383 383 383 890 889 889 889 892 891 891 891 894 893 893 893 218 217 217 217 220 219 219 219 222 221 221 221 4 1 1 1 13 15 15 15 7 5 5 5 14 15 15 15 11 10 10 10 14 15 15 15 9 10 10 10 8 5 5 5 18 17 17 17 890 889 889 889 892 891 891 891 894 893 893 893 722 721 721 721 724 723 723 723 726 725 725 725 1298 1297 1297 1297 1300 1299 1299 1299 1302 1301 1301 1301 1256 1255 1255 1255 1258 1257 1257 1257 1260 1259 1259 1259 194 193 193 193 196 195 195 195 198 197 197 197 386 385 385 385 388 387 387 387 390 389 389 389 3 1 1 1 12 10 10 10 18 17 17 17 758 757 757 757 760 759 759 759 762 761 761 761 560 559 559 559 562 561 561 561 564 563 563 563 3 1 1 1 12 10 10 10 18 17 17 17 758 757 757 757 760 759 759 759 762 761 761 761 1004 1003 1003 1003 1006 1005 1005 1005 1008 1007 1007 1007 2 1 1 1 7 5 5 5 14 15 15 15 12 10 10 10 18 17 17 17 356 355 355 355 358 357 357 357 360 359 359 359 314 313 313 313 316 315 315 315 318 317 317 317 896 895 895 895 898 897 897 897 900 899 899 899 692 691 691 691 694 693 693 693 696 695 695 695 2 1 1 1 6 5 5 5 9 10 10 10 8 5 5 5 18 17 17 17 758 757 757 757 760 759 759 759 762 761 761 761 1196 1195 1195 1195 1198 1197 1197 1197 1200 1199 1199 1199 3 1 1 1 12 10 10 10 18 17 17 17 194 193 193 193 196 195 195 195 198 197 197 197 224 223 223 223 226 225 225 225 228 227 227 227 3 1 1 1 9 10 10 10 6 5 5 5 11 10 10 10 16 15 15 15 18 17 17 17 1304 1303 1303 1303 1306 1305 1305 1305 1308 1307 1307 1307 428 427 427 427 430 429 429 429 432 431 431 431 362 361 361 361 364 363 363 363 366 365 365 365 1148 1147 1147 1147 1150 1149 1149 1149 1152 1151 1151 1151 4 1 1 1 16 15 15 15 18 17 17 17 1304 1303 1303 1303 1306 1305 1305 1305 1308 1307 1307 1307 662 661 661 661 664 663 663 663 666 665 665 665 764 763 763 763 766 765 765 765 768 767 767 767 254 253 253 256 255 255 258 257 257 896 895 895 898 897 897 900 899 899 674 673 673 676 675 675 678 677 677 548 547 547 550 549 549 552 551 551 386 385 385 388 387 387 390 389 389 4 1 1 16 15 15 18 17 17 50 49 49 52 51 51 54 53 53 134 133 133 136 135 135 138 137 137 884 883 883 886 885 885 888 887 887 92 91 91 94 93 93 96 95 95 4 1 1 16 15 15 18 17 17
这里的每个数字都代表一个transition-id, 我会在其他文章中单独讲解这个,现在可以简单理解为每个transition-id对应一个状态转移,并且可以映射到唯一的音素上,这里一共有979个,实际上如果查看对应的特征值文件的话,会发现这段语音的帧数也是979,也就是说每一个transition-id对应一帧,这就是所谓的对齐。
这个对齐文件是HMM-GMM的训练中第一个对齐文件,根据初始化模型生成,仔细看的话,他是将状态间的转移对应到1帧,然后状态内的自循环对应到3帧,也就是说预先设定好的对齐方案。事实上这是kaldi采取的一种简单粗暴的方式,直接根据状态数和帧数平均分段,并没有考虑合理性,但这是首次对齐,在后续的参数迭代中会不断生成新的对齐文件。
初始对齐结果被输入给gmm-acc-stats-ali工具中, 我们在终端运行该程序同时来看一下他的输出
gmm-acc-stats-ali --binary=false 0.mdl "$feats" ark:example_align.txt example.acc.txt
feats和之前一样,如果没关闭终端的话他应该一直保存在环境中,这里为了查看方便我们把–binary=true改为fasle,结果如下所示:
[ 0 19260 2453 2485 2422 18779 2348 2465 2467 2410 18543 2350 2411 2417 2338 18679 2482 19147 7360 577 214 575 214 574 214 157 57 157 57 157 57 189 76 187 76 187 76 354 137 354 137 354 137 29 12 29 12 29 12 352 132 352 132 352 132 194 70 194 70 194 70 425 168 423 168 422 168 203 77 203 77 203 77 646 245 646 245 646 245 24 11 24 11 24 11 484 182 481 182 481 182 361 132 361 132 361 132 271 98 270 98 268 98 539 210 539 210 539 210 10 3 10 3 10 3 326 120 326 120 326 120 295 112 295 112 294 112 221 83 221 83 221 83 340 133 339 133 339 133 19 8 19 8 19 8 201 76 200 76 200 76 170 65 170 65 170 65 393 156 392 156 392 156 515 196 515 196 515 196 0 0 0 0 0 0 1772 673 1770 673 1769 673 654 244 653 244 651 244 1313 488 1310 488 1310 488 2973 1143 2967 1143 2962 1143 73 27 73 27 73 27 330 128 330 128 328 128 106 42 105 42 104 42 692 259 692 259 691 259 834 329 832 329 832 329 537 205 536 205 533 205 102 37 102 37 102 37 146 57 146 57 145 57 181 68 181 68 180 68 305 115 305 115 305 115 5 2 5 2 5 2 256 97 253 97 253 97 424 161 424 161 424 161 127 49 127 49 127 49 113 43 113 43 113 43 92 37 92 37 92 37 354 131 353 131 351 131 444 172 443 172 441 172 137 51 136 51 136 51 133 51 133 51 132 51 6 2 6 2 6 2 203 77 203 77 203 77 39 16 39 16 39 16 181 69 181 69 181 69 38 15 37 15 37 15 960 359 958 359 958 359 1695 650 1692 650 1692 650 1748 645 1747 645 1744 645 597 221 597 221 596 221 796 318 796 318 795 318 695 272 694 272 693 272 1266 487 1264 487 1263 487 56 20 55 20 54 20 211 85 211 85 211 85 65 25 64 25 64 25 67 22 67 22 67 22 222 85 222 85 222 85 12 4 11 4 11 4 365 136 365 136 365 136 493 179 493 179 493 179 209 80 209 80 208 80 506 197 503 197 503 197 4 2 4 2 4 2 166 64 166 64 166 64 158 58 158 58 158 58 211 82 211 82 211 82 231 87 231 87 231 87 27 11 27 11 27 11 160 61 160 61 159 61 117 48 117 48 116 48 163 62 163 62 161 62 367 144 367 144 367 144 7 2 7 2 7 2 97 38 97 38 97 38 148 58 148 58 148 58 237 93 236 93 236 93 371 139 370 139 369 139 0 0 0 0 0 0 3978 1513 3971 1513 3969 1513 466 174 465 174 464 174 180 70 180 70 180 70 147 52 147 52 146 52 189 71 189 71 189 71 0 0 0 0 0 0 319 115 319 115 318 115 485 184 482 184 482 184 170 64 170 64 168 64 439 167 439 167 439 167 20 10 20 10 20 10 53 19 53 19 53 19 33 11 33 11 33 11 53 20 53 20 53 20 206 78 206 78 206 78 5 2 5 2 5 2 104 41 104 41 104 41 331 128 331 128 331 128 494 187 494 187 494 187 281 113 280 113 280 113 3 1 3 1 3 1 264 106 263 106 263 106 550 206 550 206 550 206 178 67 178 67 176 67 698 268 698 268 697 268 35 16 35 16 35 16 129 52 128 52 128 52 15 7 15 7 15 7 156 56 156 56 156 56 247 93 247 93 247 93 74 32 74 32 74 32 97 34 97 34 97 34 0 0 0 0 0 0 2182 832 2179 832 2173 832 835 318 834 318 832 318 1998 765 1992 765 1988 765 1275 493 1275 493 1272 493 1000 370 999 370 997 370 61 23 60 23 60 23 76 31 76 31 76 31 5 2 5 2 5 2 81 28 81 28 81 28 9 4 9 4 9 4 454 166 454 166 452 166 374 137 374 137 374 137 116 45 116 45 116 45 334 129 334 129 334 129 3 1 3 1 3 1 67 24 67 24 67 24 249 93 249 93 249 93 133 52 133 52 133 52 226 88 226 88 225 88 292 115 292 115 292 115 29 11 29 11 29 11 734 276 733 276 733 276 1451 546 1448 546 1447 546 839 323 837 323 835 323 888 339 886 339 885 339 2518 952 2516 952 2514 952 1313 503 1312 503 1311 503 442 164 440 164 438 164 504 192 502 192 502 192 553 207 553 207 553 207 1135 435 1133 435 1132 435 49 19 49 19 48 19 131 46 131 46 131 46 85 30 85 30 85 30 27 10 27 10 27 10 163 61 163 61 163 61 6 2 6 2 6 2 12 4 11 4 11 4 39 14 39 14 39 14 13 5 13 5 13 5 407 155 406 155 406 155 0 0 0 0 0 0 160 62 160 62 160 62 224 81 224 81 224 81 201 73 201 73 199 73 182 72 182 72 182 72 0 0 0 0 0 0 202 78 202 78 201 78 144 52 143 52 143 52 170 67 170 67 170 67 151 57 151 57 151 57 2 1 2 1 2 1 16 6 16 6 16 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 193 71 193 71 193 71 270 102 269 102 269 102 160 57 160 57 160 57 623 232 621 232 621 232 0 0 0 0 0 0 152 54 152 54 152 54 262 96 262 96 262 96 72 28 72 28 72 28 90 37 90 37 90 37 0 0 0 0 0 0 241 93 241 93 241 93 332 128 331 128 330 128 293 117 293 117 291 117 371 144 371 144 371 144 11 4 11 4 11 4 2381 886 2378 886 2374 886 246 92 244 92 244 92 236 89 235 89 235 89 298 114 298 114 296 114 399 150 399 150 399 150 0 0 0 0 0 0 35 14 35 14 35 14 507 188 506 188 506 188 86 35 86 35 86 35 90 38 90 38 90 38 0 0 0 0 0 0 39 14 39 14 39 14 150 61 150 61 150 61 8 3 8 3 8 3 417 160 417 160 416 160 6 2 6 2 6 2 65 26 64 26 64 26 108 42 108 42 108 42 0 0 0 0 0 0 188 72 188 72 188 72 3 1 3 1 3 1 1662 631 1660 631 1656 631 1783 683 1779 683 1778 683 1226 470 1224 470 1221 470 2157 817 2152 817 2147 817 ]
656 39 1 15 [ 26620 ]
[
-12902.54 -3586.418 6261.493 -613.9278 3631.588 5578.585 -3481.049 5006.469 -1383.822 6061.459 9353.521 -5700.4 2247.483 782.9587 -878.4698 -864.3397 -1582.384 -692.7347 1201.089 -553.7209 474.0117 829.1713 -1467.278 -2.107259 -452.6542 -1601.624 -54.27357 -567.8489 2.413429 213.625 278.2751 -50.79517 739.3058 267.8499 503.5899 282.9587 166.0468 880.6746 -168.3977 ]
[
6680020 6195256 6854740 7398086 8305867 6957236 4672862 5717067 5738732 4395526 4258629 4934012 2769867 154191 285055.5 289120.3 300034.2 409551.6 351125.3 293299.4 335682.4 337801.3 288190.8 279135.1 273436 195688.2 20735.76 41931.1 41908.81 44908.25 63615.12 59204.95 52904.3 58497.2 58688.16 51813.68 50639.86 47381.14 36469.82 ]
该文件存储了更新HMM和GMM模型需要的统计量,整体由两部分组成,第一行是更新转移概率需要的统计量,后面是更新GMM参数需要的统计量,每个状态都有一组,如果在文件中搜索MEANACCS 的话会发现有656个,和音素状态数是一样的,因为这里先不考虑混合高斯的情况,每个状态只有一个高斯分量。因为高斯模型需要更新的参数只有均值向量和协方差矩阵,所以每一组状态的统计量是MEANACCS和DIAGVARACCS。
2. GMM模型迭代
下面开始完整的模型参数更新,用的是EM算法,在其他文章中我会尽可能结合公式和Kaldi的C++代码来讲解详细的过程,毕竟这是HMM-GMM训练的核心部分,在这里暂时不深入讨论。
if [ $stage -le 0 ]; then
gmm-est --min-gaussian-occupancy=3 --mix-up=$numgauss --power=$power \
$dir/0.mdl "gmm-sum-accs - $dir/0.*.acc|" $dir/1.mdl 2> $dir/log/update.0.log || exit 1;
rm $dir/0.*.acc
fi
gmm-est对GMM参数进行最大似然估计,我们单独执行它,注意脚本中有一段是 gmm-sum-accs而我们执行时没有,因为当前我们只有一部分数据,准确说是1/20的训练数据,所以这里不需要讲统计量汇总。
gmm-est --min-gaussian-occupancy=3 --mix-up=656 --power=0.25 0.mdl example.acc example_1.mdl
example_1.mdl 就是对初始化模型0.mdl 的一次迭代,和前面一样如果用gmm-copy查看的话会发现参数发生了变化,但高斯分量的总数还是656。重复下面的步骤直到指定的迭代次数即可完成monophone模型的训练:
while [ $x -lt $num_iters ]; do
echo "$0: Pass $x"
if [ $stage -le $x ]; then
if echo $realign_iters | grep -w $x >/dev/null; then
echo "$0: Aligning data"
mdl="gmm-boost-silence --boost=$boost_silence `cat $lang/phones/optional_silence.csl` $dir/$x.mdl - |"
$cmd JOB=1:$nj $dir/log/align.$x.JOB.log \
gmm-align-compiled $scale_opts --beam=$beam --retry-beam=$retry_beam --careful=$careful "$mdl" \
"ark:gunzip -c $dir/fsts.JOB.gz|" "$feats" "ark,t:|gzip -c >$dir/ali.JOB.gz" \
|| exit 1;
fi
$cmd JOB=1:$nj $dir/log/acc.$x.JOB.log \
gmm-acc-stats-ali $dir/$x.mdl "$feats" "ark:gunzip -c $dir/ali.JOB.gz|" \
$dir/$x.JOB.acc || exit 1;
$cmd $dir/log/update.$x.log \
gmm-est --write-occs=$dir/$[$x+1].occs --mix-up=$numgauss --power=$power $dir/$x.mdl \
"gmm-sum-accs - $dir/$x.*.acc|" $dir/$[$x+1].mdl || exit 1;
rm $dir/$x.mdl $dir/$x.*.acc $dir/$x.occs 2>/dev/null
fi
if [ $x -le $max_iter_inc ]; then
numgauss=$[$numgauss+$incgauss];
fi
beam=$regular_beam
x=$[$x+1]
done
我们尝试改写一下代码,让他只对一部分数据进行训练,然后我们查看结果,虽然最后的对齐结果可能会不太理想,但是他一定比首次对齐的效果要好。这里需要新建一个shell脚本,然后自己添加一些变量,大体上和上面的代码是一样的,只不过所有的$cmd都要去掉,因为现在不需要分布式处理。修改后的代码如下:
lang=../../../data/lang
sdata=../../../data/mfcc/train/split20
feats="ark,s,cs:apply-cmvn --utt2spk=ark:$sdata/1/utt2spk scp:../example_cmvn.scp scp:../example_feats.scp ark:- | add-deltas ark:- ark:- |"
beam=6
x=1
num_iters=40
max_iter_inc=30
totgauss=1000
stage=-4
power=0.25
boost_silence=1
realign_iters="1 2 3 4 5 6 7 8 9 10 12 14 16 18 20 23 26 29 32 35 38"
careful=false
retry_beam=40
regular_beam=10
scale_opts="--transition-scale=1.0 --acoustic-scale=0.1 --self-loop-scale=0.1"
numgauss=`gmm-info --print-args=false 0.mdl | grep gaussians | awk '{print $NF}'`
incgauss=$[($totgauss-$numgauss)/$max_iter_inc] # per-iter increment for #Gauss
while [ $x -lt $num_iters ]; do
echo "$0: Pass $x"
if [ $stage -le $x ]; then
if echo $realign_iters | grep -w $x >/dev/null; then
echo "$0: Aligning data"
mdl="gmm-boost-silence --boost=$boost_silence `cat $lang/phones/optional_silence.csl` $x.mdl - |"
gmm-align-compiled $scale_opts --beam=$beam --retry-beam=$retry_beam --careful=$careful "$mdl" \
ark:fsts.1 "$feats" ark,t:ali.1 2>>ali.log || exit 1;
fi
gmm-acc-stats-ali $x.mdl "$feats" ark:ali.1 $x.1.acc 2>acc.log || exit 1;
gmm-est --write-occs=$[$x+1].occs --mix-up=$numgauss --power=$power $x.mdl \
"gmm-sum-accs - $x.*.acc|" $[$x+1].mdl 2>est.log || exit 1;
# rm $x.mdl $x.*.acc $x.occs 2>/dev/null
fi
if [ $x -le $max_iter_inc ]; then
numgauss=$[$numgauss+$incgauss];
fi
beam=$regular_beam
x=$[$x+1]
done
建议单独新建一个目录,否则生成的模型和日志文件会和原来的混淆,比如我就在exp/mono/下面新建了一个example目录,注意lang和sdata需要修改。可以看到这段代码一直在重复对齐,计算统计量,参数更新这个过程。最后可以看到生成了40个模型文件和40个统计量文件,对齐文件少了一些因为源代码中有realign_iter的参数存在,他不是每次迭代都重新对齐一次。下面我们通过对数似然来看一下训练效果,对数似然值保存在每次的对齐结果中,我们通过cat ali.log | grep log-likelihood 来显示对数似然的变化过程:
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -108.601 over 459112 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -103.055 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -100.783 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -99.7632 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -99.086 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -98.566 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -98.1211 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -97.7789 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -97.5269 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -97.3522 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -97.1358 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.937 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.7904 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.6923 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.593 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.4382 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.3326 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.2175 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.1289 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.0494 over 463379 frames.
LOG (gmm-align-compiled[5.5]:main():gmm-align-compiled.cc:135) Overall log-likelihood per frame is -96.0193 over 463379 frames.
可以看到即便是以很少量的数据去训练单音子模型,在EM算法中对大似然估计的优化下对数似然度也有增加的趋势,以上就是单因子模型的训练全过程,官方脚本中删除了中间的模型和统计量的保存文件,所以最后只能看到final.mdl和对齐结果。
最后我们用gmm-info 看一下最终模型:
gmm-info 40.mdl
number of phones 218
number of pdfs 656
number of transition-ids 1320
number of transition-states 656
feature dimension 39
number of gaussians 987
可以看到高斯分量的数目是987,意味着有的状态高斯分量增加了,虽然设定是1000,但实际上会少一部分。
总结
train_mono.sh 的解读到此就结束了,后面的文章中会更新单音素模型的解码部分,并且按照run.sh里面的顺序逐步对三音子模型以及说话人适应模型的训练进行解读,不过说实话,kaldi的C++源码不太容易懂,可能是自己的代码功底比较薄弱,我会尽可能结和EM算法的公式去理解一下C++源码。
本文主要参考了《Kaldi语音识别实战》这本书,对kaldi的理解很有帮助。