论文阅读《LoFTR: Detector-Free Local Feature Matching with Transformers》

论文地址：https://arxiv.org/pdf/2104.00680.pdf
代码地址：https://github.com/zju3dv/LoFTR

---

背景

  本文提出了一种新的局部图像特征匹配方法，通过先在粗层次上建立像素级密集匹配，然后在更细的层次上进行细化，并利用transformer的自注意层和交叉注意力层来获取基于两幅图像的特征描述符。本文的创新点在于Transformer提供的全局感受野使得该方法能够在低纹理区域产生密集匹配。

---

模型结构

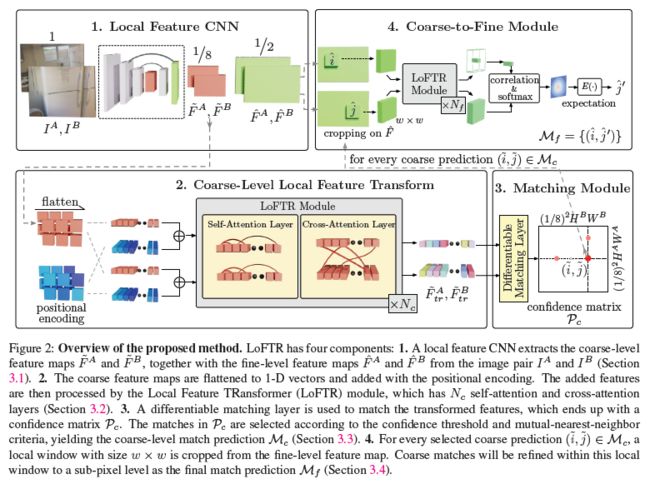
  基于特征检测器的检测方法可以减少进行匹配时的搜索空间，而在无纹理或重复纹理地区，特征检测器难以检测出有效的特征，这回极大影响后续的匹配过程的效率；

  无检测器（Detector free）的方法通过建立像素级别的密集匹配来解决这个问题，通过从密集匹配中保留置信度较高的匹配来避免特征检测。然而使用CNN来提取的密集特征的感受野有限，在无纹理区域的效果较差。而人类在这些区域会同时考虑局部信息与全局信息；
  基于此，本文提出一个Local Feature Transformer（LoFTR）：先在低分辨率的特征图上进行密集匹配，然后保留置信度较高的匹配，然后将其细化到高分率的密集匹配；同时使用自注意力与交叉注意力来得到更加具有特异性的匹配特征；LoFTR可以在弱纹理、运动模糊与重复纹理区域产生较高质量的匹配；

局部特征提取

  使用权值共享的FPN结构的CNN特征提取模块从两幅图像中得到 $\frac{1}{8}$ 原图大小的低分辨率的特征图 ${\tilde{F}}^A与{\tilde{F}}^B$，同时得到 $\frac{1}{2}$ 原图大小的高分辨率的特征图 ${\hat{F}}^A与{\hat{F}}^B$ ;CNN的局部空间不变性较适合用于局部特征提取；

局部特征转换（LoFTR）模块

  得到低分辨率的特征图 ${\tilde{F}}^A与{\tilde{F}}^B$ 后，将其与位置送进局部特征转换模块得到具有特异性的匹配特征${\tilde{F}}_{tr}^A与{\tilde{F}}_{tr}^B$，局部特征转换模块包含位置编码模块、自注意力与交叉注意力特征增强模块；

位置编码模块

  受到DETR的启发，采用sin函数进行位置编码，将位置信息编码成特定的向量，与输入的 ${\tilde{F}}^A与{\tilde{F}}^B$ 展开后的特征进行融合，融合后的特征既同时包含位置信息与深度特征信息；

自注意力模块与交叉注意力模块

  此处不再赘述，可以参考博主上一篇博客“论文阅读《SuperGlue: Learning Feature Matching with Graph Neural Networks》”中的GNN模块的解读，此处简单讲讲Transformer；

Transformer：

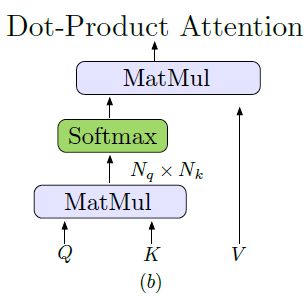
  Transformer 由顺序连接的注意力层组成，其核心是注意力模块的使用，Transformer的输入为query、key、value，与数据检索的过程类似，数据库的的数据为value，对于每一条数据 V 其对应的索引键值为向量K，先由查询向量与键值向量求相似度，再由相似矩阵来对value中的V向量加权求和，得到最后的输出，这个过程也被称为图神经网络中的“消息传递”。如式1所示：
$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(Q{K}^T\right)V\text{\hspace{1em}(1)}$$

Linear Transformer：
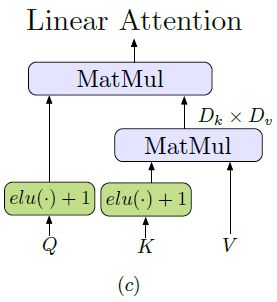
  若查询向量 Q 与键值 K 均拥有N条，且每个特征的长度为 D ，则求相似性矩阵时候的计算复杂度为 $O(N^2)$，这时候需要使用Linear Transformer来降低计算相似度，将计算复杂度降低到了 $O(N)$， 其中 $elu(.)$ 表示核函数：
$$\begin{gathered} sim(Q,K)=\varphi (Q)\cdot \varphi (K{)}^T \\ \varphi (.)=elu(.)+1\text{\hspace{1em}(2)} \end{gathered}$$

粗粒度（低分辨率）匹配

  经过L层自注意力模块与交叉注意力模迭代特征增强，得到的输出匹配特征可以用于匹配，可以参考SuperGlue中的将其转换为可微的最优传输问题来处理，也可以使用dual-softmax来处理，由输出向量计算匹配得分矩阵：
$$\mathcal{S}(i,j)=\frac{1}{\tau }\cdot ⟨{\tilde{F}}_{tr}^A(i),{\tilde{F}}_{tr}^B(j)⟩\text{\hspace{1em}(3)}$$
  若采用求解最优传输的方式来进行匹配，则依然参考博主上一篇博客“论文阅读《SuperGlue: Learning Feature Matching with Graph Neural Networks》”中的最优匹配模块的解读，再次不再赘述；
  此外，还可以在得分矩阵 S 的两个维度上进行softmax得到匹配概率矩阵 ${\mathcal{P}}_c$
$${\mathcal{P}}_c(i,j)=\mathrm{softmax}(\mathcal{S}(i,\cdot ){)}_j\cdot \mathrm{softmax}(\mathcal{S}(\cdot ,j){)}_i\text{\hspace{1em}(4)}$$
筛选匹配对：
  基于置信度来筛选置信度高于 ${\theta }_c$ 的匹配点，并使用相互最近邻准则（左右一致性检查+最优与次优有一定距离）来剔除外点，如式5所示：
$${\mathcal{M}}_c=\left\{(\tilde{i},\tilde{j})\mid \forall (\tilde{i},\tilde{j})\in \mathrm{MNN}\left({\mathcal{P}}_c\right),{\mathcal{P}}_c(\tilde{i},\tilde{j})\ge {\theta }_c\right\}\text{\hspace{1em}(5)}$$

从粗糙到精细的优化模块

在建立了粗粒度的匹配后，使用一种基于相关性的方法来完成从粗粒度到细粒度的转换；

1. 首先将粗匹配点对$\tilde{i}与\tilde{j}$ 投影回细粒度的特征图上 ${\hat{F}}^A$ 得到点 $\hat{i}$ 与 ${\hat{F}}^B$ 上得到点 $\hat{j}$；
2. 在细粒度特征图的特征点处裁剪一个 $w\times w$ 的局部窗口；再将这个局部窗口输入到LOFTR模块（位置编码+自注意力+交叉注意力）中得到一对局部特征图 ${\hat{F}}_{tr}^A(\hat{i})与{\hat{F}}_{tr}^B(\hat{j})$；
3. 计算局部窗口特征图 ${\hat{F}}_{tr}^A(\hat{i})与{\hat{F}}_{tr}^B(\hat{j})$ 的相关性得分矩阵；
4. 通过计算概率分布上的期望，得到 $\hat{i}$ 在图 $I_B$ 上亚像素精度的匹配特征点的位置 ${\hat{j}}^{\prime }$。

---

损失函数

  损失函数包含粗粒度损失与细粒度损失：
$$\mathcal{L}={\mathcal{L}}_c+{\mathcal{L}}_f\text{\hspace{1em}(6)}$$
其中粗粒度损失对匹配概率矩阵求负对数似然：$${\mathcal{L}}_c=-\frac{1}{\left|{\mathcal{M}}_c^{gt}\right|}\sum _{(\tilde{i},\tilde{j})\in {\mathcal{M}}_c^{gt}}\log {\mathcal{P}}_c(\tilde{i},\tilde{j})\text{\hspace{1em}(7)}$$
细粒度损失采用 $L_2$ 损失，对于每个点 $\hat{i}$ 在局部窗口的方差 ${\sigma }^2(\hat{i})$ 来对每个匹配点进行加权，从而得到损失函数：
$${\mathcal{L}}_f=\frac{1}{\left|{\mathcal{M}}_f\right|}\sum _{\left(\hat{i},{\hat{j}}^{\prime }\right)\in {\mathcal{M}}_f}\frac{1}{{\sigma }^2(\hat{i})}{\Vert {\hat{j}}^{\prime }-{\hat{j}}_{gt}^{\prime }\Vert }_2\text{\hspace{1em}(8)}$$
其中 ${\hat{j}}_{gt}^{\prime }$ 是通过使用相机内外参与深度图，将 $I_A$ 的 $\hat{i}$ 点的特征warp到 $I_B$ 的 ${\hat{j}}_{gt}^{\prime }$ 点，与 ${\hat{j}}^{\prime }$ 点的特征向量求 $L_2$ 损失；

---

实验结果