Datawhale学习笔记-吃瓜笔记:决策树
决策树
基本流程
决策树是一类常见的机器学习方法,以二分类任务为例,我们希望从给定训练数据集学得一个模型用以对新示例进行分类,这个把样本分类的任务,可看作对“当前样本属于正类吗?”这个问题的“决策”或“判定”过程,顾名思义,决策树是基于树结构来进行决策的,这恰是人类在面临决策问题时的一种很自然的处理机制。
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。在机器学习中,决策树是一个预测模型,他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
分类树(决策树)是一种十分常用的分类方法。它是一种监督学习,所谓监督学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。
决策树的组成
决策点,是对几种可能方案的选择,即最后选择的最佳方案。如果决策属于多级决策,则决策树的中间可以有多个决策点,以决策树根部的决策点为最终决策方案。
状态节点,代表备选方案的经济效果(期望值),通过各状态节点的经济效果的对比,按照一定的决策标准就可以选出最佳方案。由状态节点引出的分支称为概率枝,概率枝的数目表示可能出现的自然状态数目每个分枝上要注明该状态出现的概率。
结果节点,将每个方案在各种自然状态下取得的损益值标注于结果节点的右端。
决策树画法
机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术,可以用于分析数据,同样也可以用来作预测。
从数据产生决策树的机器学习技术叫做决策树学习, 通俗说就是决策树。
一个决策树包含三种类型的节点:
1.决策节点:通常用矩形框来表示
2.机会节点:通常用圆圈来表示
3.终结点:通常用三角形来表示
决策树学习也是资料探勘中一个普通的方法。在这里,每个决策树都表述了一种树型结构,它由它的分支来对该类型的对象依靠属性进行分类。每个决策树可以依靠对源数据库的分割进行数据测试。这个过程可以递归式的对树进行修剪。 当不能再进行分割或一个单独的类可以被应用于某一分支时,递归过程就完成了。另外,随机森林分类器将许多决策树结合起来以提升分类的正确率。
决策树同时也可以依靠计算条件概率来构造。
决策树如果依靠数学的计算方法可以取得更加理想的效果。 数据库已如下所示:
(x, y) = (x1, x2, x3…, xk, y)
相关的变量 Y 表示我们尝试去理解,分类或者更一般化的结果。 其他的变量x1, x2, x3 等则是帮助我们达到目的的变量。
决策树的剪枝
剪枝是决策树停止分支的方法之一,剪枝有分预先剪枝和后剪枝两种。预先剪枝是在树的生长过程中设定一个指标,当达到该指标时就停止生长,这样做容易产生“视界局限”,就是一旦停止分支,使得节点N成为叶节点,就断绝了其后继节点进行“好”的分支操作的任何可能性。不严格的说这些已停止的分支会误导学习算法,导致产生的树不纯度降差最大的地方过分靠近根节点。后剪枝中树首先要充分生长,直到叶节点都有最小的不纯度值为止,因而可以克服“视界局限”。然后对所有相邻的成对叶节点考虑是否消去它们,如果消去能引起令人满意的不纯度增长,那么执行消去,并令它们的公共父节点成为新的叶节点。这种“合并”叶节点的做法和节点分支的过程恰好相反,经过剪枝后叶节点常常会分布在很宽的层次上,树也变得非平衡。后剪枝技术的优点是克服了“视界局限”效应,而且无需保留部分样本用于交叉验证,所以可以充分利用全部训练集的信息。但后剪枝的计算量代价比预剪枝方法大得多,特别是在大样本集中,不过对于小样本的情况,后剪枝方法还是优于预剪枝方法的。
决策树的优点
决策树易于理解和实现,人们在在学习过程中不需要使用者了解很多的背景知识,这同时是它的能够直接体现数据的特点,只要通过解释后都有能力去理解决策树所表达的意义。
对于决策树,数据的准备往往是简单或者是不必要的,而且能够同时处理数据型和常规型属性,在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
易于通过静态测试来对模型进行评测,可以测定模型可信度;如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。
决策树的缺点
1)对连续性的字段比较难预测。
2)对有时间顺序的数据,需要很多预处理的工作。
3)当类别太多时,错误可能就会增加的比较快。
4)一般的算法分类的时候,只是根据一个字段来分类。
ID3决策树
自信息:
I ( X ) = − log b p ( x ) I(X)=-\log_{b}{p(x)} I(X)=−logbp(x)
当 b = 2 b=2 b=2时单位为bit,当 b = e b=e b=e时单位为nat
信息熵(自信息的期望):度量随机变量 X X X的不确定性,信息熵越大越不确定
H ( X ) = E [ I ( X ) ] = − ∑ x p ( x ) log b p ( x ) H(X)=E[I(X)]=-\sum_{x}p(x)\log_{b}p(x) H(X)=E[I(X)]=−∑xp(x)logbp(x) (此处以离散型为例)
计算信息熵时约定:若 p ( x ) = 0 p(x)=0 p(x)=0,则 p ( x ) log b p ( x ) = 0 p(x)\log_{b}p(x)=0 p(x)logbp(x)=0。当 X X X的某个取值的概率为1
时信息熵最小(最确定),其值为0;当 X X X的各个取值的概率均等时信息熵最大(最不确
定),其值为 log b ∣ X ∣ \log_{b}|X| logb∣X∣,其中 ∣ X ∣ |X| ∣X∣表示可能取值的个数。
将样本类别标记 y y y视作随机变量,各个类别在样本集合 D D D中的占比 p k ( k = 1 , 2 , . . . , ∣ y ∣ ) p_{k}(k=1,2,...,|y|) pk(k=1,2,...,∣y∣)
视作各个类别取值的概率,则样本集合 D D D(随机变量 y y y)的信息熵(底数取2)为
log b ∣ X ∣ Ent ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k \log_{b}|X|\operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k} logb∣X∣Ent(D)=−∑k=1∣Y∣pklog2pk
此时的信息熵所代表的“不确定性”可以转换理解为集合内样本的“纯度”(举个栗子)
条件熵( Y Y Y的信息熵关于概率分布 X X X的期望):在已知 X X X后 Y Y Y的不确定性
H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) H(Y|X)=\sum_{x}p(x)H(Y|X=x) H(Y∣X)=∑xp(x)H(Y∣X=x)
从单个属性(特征) a a a的角度来看,假设其可能取值为 a 1 , a 2 , . . . , a V , D v {a^1,a^2,...,a^V},D^v a1,a2,...,aV,Dv表示属性 a a a
取值为 a v ∈ { a 1 , a 2 , … , a V } a^{v} \in\left\{a^{1}, a^{2}, \ldots, a^{V}\right\} av∈{a1,a2,…,aV}的样本集合, ∣ D v ∣ ∣ D ∣ \frac{\left|D^{v}\right|}{|D|} ∣D∣∣Dv∣表示占比,那么在已知属性 a a a的取值后,样本集合 D D D的条件熵为
∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) \sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) ∑v=1V∣D∣∣Dv∣Ent(Dv)
信息增益:在已知属性(特征) a a a的取值后 y y y的不确定性减少的量,也即纯度的提升
Gain ( D , a ) = Ent ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) \operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) Gain(D,a)=Ent(D)−∑v=1V∣D∣∣Dv∣Ent(Dv)
ID3决策树:以信息增益为准则来选择划分属性的决策树
a ∗ = arg max a ∈ A Gain ( D , a ) a_{*}=\underset{a \in A}{\arg \max } \operatorname{Gain}(D, a) a∗=a∈AargmaxGain(D,a)
代码实现
C4.5决策树
信息增益准则对可能取值数目较多的属性有所偏好(例如“编号”这个较为极端的例子,不
过其本质原因不是取值数目过多,而是每个取值里面所包含的样本量太少),为减少这
种偏好可能带来的不利影响,C4.5决策树选择使用“增益率”代替“信息增益”,增益率定义
为
Gain_ratio ( D , a ) = Gain ( D , a ) IV ( a ) (D, a)=\frac{\operatorname{Gain}(D, a)}{\operatorname{IV}(a)} (D,a)=IV(a)Gain(D,a)
其中
IV ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log 2 ∣ D v ∣ ∣ D ∣ \operatorname{IV}(a)=-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \log _{2} \frac{\left|D^{v}\right|}{|D|} IV(a)=−∑v=1V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性 a a a的“固有值”, a a a的可能取值个数 V V V越大,通常其固有值 I V ( a ) IV(a) IV(a)也越大。但是,
增益率对可能取值数目较少的属性有所偏好。
因此,C4.5决策树并未完全使用“增益率”代替“信息增益”,而是采用一种启发式的方法:
先选出信息增益高于平均水平的属性,然后再从中选择增益率最高的。
CART决策树
基尼值:从样本集合 D D D中随机抽取两个样本,其类别标记不一致的概率。因此,基尼值
越小,碰到异类的概率就越小,纯度自然就越高。
Gini ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = ∑ k = 1 ∣ Y ∣ p k ( 1 − p k ) = 1 − ∑ k = 1 ∣ Y ∣ p k 2 \begin{aligned} \operatorname{Gini}(D) &=\sum_{k=1}^{|\mathcal{Y}|} \sum_{k^{\prime} \neq k} p_{k} p_{k^{\prime}} \\ \\ &=\sum_{k=1}^{|\mathcal{Y}|} p_{k}\left(1-p_{k}\right) \\ \\ &=1-\sum_{k=1}^{|\mathcal{Y}|} p_{k}^{2} \end{aligned} Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=k=1∑∣Y∣pk(1−pk)=1−k=1∑∣Y∣pk2
属性的 a a a基尼指数(类比信息熵和条件熵):
Gini_index ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Gini ( D v ) (D, a)=\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Gini}\left(D^{v}\right) (D,a)=∑v=1V∣D∣∣Dv∣Gini(Dv)
CART决策树:选择基尼指数最小的属性作为最优划分属性
a ∗ = arg min a ∈ A a_{*}=\underset{a \in A}{\arg \min } a∗=a∈AargminGini_index ( D , a ) (D, a) (D,a)
CART决策树的实际构造算法如下:
首先,对每个属性 a a a的每个可能取值 v v v,将数据集 D D D分为 a = v a=v a=v和 a ≠ v a \ne v a=v两部分来计
算基尼指数,即
Gini_index ( D , a ) = ∣ D a = v ∣ ∣ D ∣ (D,a)=\frac{|D^{a=v}|}{|D|} (D,a)=∣D∣∣Da=v∣Gini ( D a = v ) + ∣ D a ≠ v ∣ ∣ D ∣ (D^{a=v})+\frac{|D^{a\ne v}|}{|D|} (Da=v)+∣D∣∣Da=v∣Gini ( D a ≠ v ) (D^{a\ne v}) (Da=v)
然后,选择基尼指数最小的属性及其对应取值作为最优划分属性和最优划分点;
最后,重复以上两步,直至满足停止条件。
使用SKlearn中graphviz包实现决策树的绘制
import numpy as np
import pandas as pd
#香农熵的python代码
def calEnt(dataSet):
n = dataSet.shape[0] #数据集总行数
iset = dataSet.iloc[:,-1].value_counts() #标签的所有类别
p = iset/n #每一类标签所占比
ent = (-p*np.log2(p)).sum() #计算信息熵
return ent
#创建数据集
def createDataSet():
row_data = {'no surfacing':[1,1,1,0,0],
'flippers':[1,1,0,1,1],
'fish':['yes','yes','no','no','no']}
dataSet = pd.DataFrame(row_data)
return dataSet
dataSet = createDataSet()
print(dataSet)
"""
函数功能:根据信息增益选择出最佳数据集切分的列
参数说明:
dataSet:原始数据集
返回:
axis:数据集最佳切分列的索引
"""
#选择最优的列进行切分
def bestSplit(dataSet):
baseEnt = calEnt(dataSet) #计算原始熵
bestGain = 0 #初始化信息增益
axis = -1 #初始化最佳切分列,标签列
for i in range(dataSet.shape[1]-1): #对特征的每一列进行循环
levels= dataSet.iloc[:,i].value_counts().index #提取出当前列的所有取值
ents = 0 #初始化子节点的信息熵
for j in levels: #对当前列的每一个取值进行循环
childSet = dataSet[dataSet.iloc[:,i]==j] #某一个子节点的dataframe
ent = calEnt(childSet) #计算某一个子节点的信息熵
ents += (childSet.shape[0]/dataSet.shape[0])*ent #计算当前列的信息熵
#print(f'第{i}列的信息熵为{ents}')
infoGain = baseEnt-ents #计算当前列的信息增益
#print(f'第{i}列的信息增益为{infoGain}')
if (infoGain > bestGain):
bestGain = infoGain #选择最大信息增益
axis = i #最大信息增益所在列的索引
return axis
"""
函数功能:基于最大信息增益切分数据集,递归构建决策树
参数说明:
dataSet:原始数据集(最后一列是标签)
返回:
myTree:字典形式的树
"""
def createTree(dataSet):
featlist = list(dataSet.columns) #提取出数据集所有的列
classlist = dataSet.iloc[:,-1].value_counts() #获取最后一列类标签
#判断最多标签数目是否等于数据集行数,或者数据集是否只有一列
if classlist[0]==dataSet.shape[0] or dataSet.shape[1] == 1:
return classlist.index[0] #如果是,返回类标签
axis = bestSplit(dataSet) #确定出当前最佳切分列的索引
bestfeat = featlist[axis] #获取该索引对应的特征
myTree = {bestfeat:{}} #采用字典嵌套的方式存储树信息
del featlist[axis] #删除当前特征
valuelist = set(dataSet.iloc[:,axis]) #提取最佳切分列所有属性值
for value in valuelist: #对每一个属性值递归建树
myTree[bestfeat][value] = createTree(mySplit(dataSet,axis,value))
return myTree
"""
函数功能:按照给定的列划分数据集
参数说明:
dataSet:原始数据集
axis:指定的列索引
value:指定的属性值
返回:
redataSet:按照指定列索引和属性值切分后的数据集
"""
def mySplit(dataSet,axis,value):
col = dataSet.columns[axis]
redataSet = dataSet.loc[dataSet[col]==value,:].drop(col,axis=1)
return redataSet
#导入相应的包
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
import graphviz
#特征
Xtrain = dataSet.iloc[:,:-1]
#标签
Ytrain = dataSet.iloc[:,-1]
labels = Ytrain.unique().tolist()
Ytrain = Ytrain.apply(lambda x: labels.index(x)) #将本文转换为数字
#绘制树模型
clf = DecisionTreeClassifier()
clf = clf.fit(Xtrain, Ytrain)
tree.export_graphviz(clf)
dot_data = tree.export_graphviz(clf, out_file=None)
graphviz.Source(dot_data)
#给图形增加标签和颜色
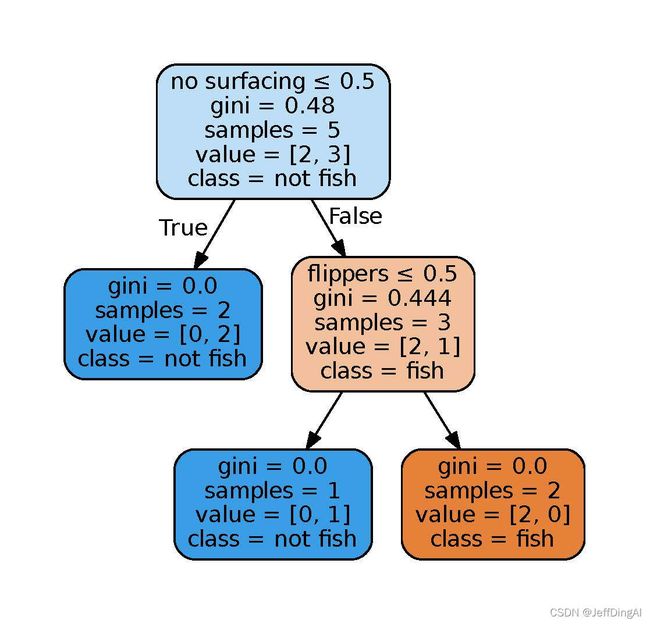
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=['no surfacing', 'flippers'],
class_names=['fish', 'not fish'],
filled=True, rounded=True,
special_characters=True)
graphviz.Source(dot_data)
#利用render方法生成图形
graph = graphviz.Source(dot_data)
graph.render("fish")