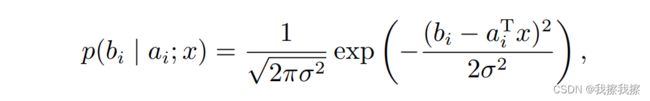(最优化理论与方法)第三章优化建模-第二节:回归分析
文章目录
- 一:概述
-
- (1)回归分析概述
- (2)回归分析描述
- (3)常见回归分析类型
- (4)过拟合和欠拟合
- 二:线性回归模型
-
- (1)线性回归模型
- (2)正则化线性回归模型
-
- ①:Tikhonov正则化
- ②:LASSO问题及其变形
一:概述
(1)回归分析概述
回归分析:在统计学和大数据中回归分析的定义分别为
- 统计学:指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照设计变量多少,分为一元回归和多元回归分析;按照因变量的多少,可以分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系,可以分为线性回归分析和非线性回归分析
- 大数据:在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系
(2)回归分析描述
回归分析:一般的回归分析可以写成如下形式,其含义为响应变量 b b b与自变量 a a a通过函数 f f f联系在一起
b = f ( a ) + ξ b=f(a)+\xi b=f(a)+ξ
- a ∈ R d a\in R^{d} a∈Rd为自变量
- b ∈ R b\in R b∈R为响应变量
- ξ \xi ξ是模型的噪声(误差)
- 在实际问题中,一般只能知道 a a a和 b b b的观测值,而误差 ξ \xi ξ是未知的
建立回归分析的最终任务是利用 m m m个观测值 ( a i , b i ) (a_{i},b_{i}) (ai,bi)来求解出 f f f的具体形式,然后对新观测的自变量对响应变量做出预测
函数 f f f取值于函数空间中,为了缩小 f f f的范围,一般会将其进行参数化,于是上述模型转变为
b = f ( a ; x ) + ξ b=f(a;x)+\xi b=f(a;x)+ξ
- f ( a ; x ) f(a;x) f(a;x)含义为 f f f以 x ∈ R n x\in R^{n} x∈Rn为参数,通过选取不同的 x x x得到不同的 f f f
参数化的意义在于将 f f f选取的范围缩小到了有限维空间 R n R^{n} Rn中,求解函数 f f f的过程实际上就是求解参数 x x x的过程
(3)常见回归分析类型
线性回归(Linear Regression):这是最为熟知的建模技术之一,也是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的
逻辑回归(Logistic Regression):用来计算 “事件=Success”和“事件=Failure”的概率。当因变量的类型属于二元(1/0,真/假,是/否)变量时,应该使用逻辑回归
多项式回归(Polynomial Regression):对于一个回归方程,如果自变量的指数大于1,那么它就是多项式回归方程。例如 y = a + b x 2 y=a+bx^{2} y=a+bx2。在这种回归技术中,最佳拟合线不是直线,而是曲线
逐步回归(Stepwise Regression):在处理多个自变量时,可以使用这种形式的回归。在这种技术中,自变量的选择是在一个自动的过程中完成的,其中包括非人为操作。这种建模技术的目的是使用最少的预测变量数来最大化预测能力
岭回归(Ridge Regression):当数据之间存在多重共线性(自变量高度相关) 时,就需要使用岭回归进行分析。在存在多重共线性时,尽管最小二乘法测得的估计值不存在偏差,它们的方差也会很大,从而使得观测值与真实值相差甚远。岭回归通过给回归估计值添加一个偏差值,来降低标准误差
Lasso回归(Lasso Regression):类似于岭回归,Lasso回归也会就回归系数向量给出惩罚值项。此外,它能够减少变化程度并提高线性回归的模型。Lasso回归与Ridge回归不同的是,它使用的乘法函数是 l 1 l_{1} l1范数而不是 l 2 l_{2} l2范数。这导致惩罚值使一些参数估计结果等于0,使用的惩罚值越大,进一步估计会使得缩小值越趋于0,这导致要从给定的 n n n个变量中选择变量
弹性网络回归(ElasticeNet Regression):是Lasso和Ridge回归技术的混合体。它使用 L 1 L1 L1来训练并且 L 2 L2 L2优先作为正则化矩阵。当有多个相关的特征时,弹性网络回归是很有用的
(4)过拟合和欠拟合
什么才算好的模型:一个好的模型需要有比较优秀的预测能力,即我们需要将 f f f作用在测试集数据上,计算其预测误差
- 过拟合:对训练数据拟合效果非常好,但在测试数据上效果却很差
- 欠拟合:对训练数据拟合效果都很差,构建的 f f f必不能完全解释 a a a和 b b b之间的依赖关系
总的来说,一个好的模型要同时兼顾两个方面,即在测试数据上的预测误差小,同时具有简单的形式
二:线性回归模型
(1)线性回归模型
线性回归:设 ( w i , b i ) (w_{i},b_{i}) (wi,bi)为观测到的自变量与响应变量,且不同数据点相互独立,则对每个数据点
b i = w i 1 x 1 + w i 2 x 2 + . . . + w i 1 x 1 + w i 2 x 2 + w i , n − 1 x n − 1 + x n , i = 1 , 2 , . . . , m b_{i}=w_{i1}x_{1}+w_{i2}x_{2}+...+w_{i1}x_{1}+w_{i2}x_{2}+w_{i,n-1}x_{n-1}+x_{n},i=1,2,...,m bi=wi1x1+wi2x2+...+wi1x1+wi2x2+wi,n−1xn−1+xn,i=1,2,...,m
- x i x_{i} xi是需要确定的参数
- ξ i \xi_{i} ξi是某种噪声且不同数据点之间相互独立
将训练集中的输入特征加上常数项 1 1 1(对应元素为 x n x_{n} xn),写成 a i = ( w i T 1 ) a_{i}=(w_{i}^{T} 1) ai=(wiT1),令 x = ( x 1 , x 2 , . . . , x n ) T ∈ R n x=(x_{1},x_{2},...,x_{n})^{T}\in R^{n} x=(x1,x2,...,xn)T∈Rn,则线性回归模型可简写为
b i = a i T x + ξ i b_{i}=a_{i}^{T}x+\xi_{i} bi=aiTx+ξi
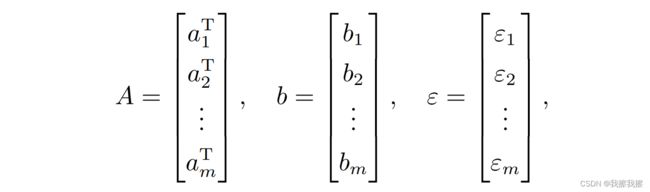
使用矩阵表示更为简洁,所以我们将训练集中的输入特征写成一个 m × n m×n m×n矩阵 A A A,将标签 b i b_{i} bi和噪声 ξ i \xi_{i} ξi写成向量形式,也即
得到其矩阵形式
b = A x + ξ b=Ax+\xi b=Ax+ξ
假设 ξ i \xi_{i} ξi是高斯白噪声,即 ξ ∼ N ( 0 , σ 2 ) \xi\sim N(0, \sigma^{2}) ξ∼N(0,σ2),则有
于是对数似然函数为
最大似然估计则是极大化对数似然函数,去掉除常数项之后我们得到如下最小二乘问题
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 \mathop{min}\limits_{x\in R^{n}}\frac{1}{2}||Ax-b||^{2}_{2} x∈Rnmin21∣∣Ax−b∣∣22
- 注意:构建最大似然估计时无需知道 ξ \xi ξ的方差 σ 2 \sigma^{2} σ2
以上变形最重要的意义是建立了最小二乘法和回归分析的联系,当假设误差是高斯白噪声时,最小二乘解就是线性回归模型的最大似然解。但当假设误差不是高斯白噪声时,则需要借助似然函数来构造其他噪声所对应的目标函数
(2)正则化线性回归模型
①:Tikhonov正则化
Tikhonov正则化:为了平衡模型的拟合性质和解的光滑性,Tikhonov正则化或岭回归添加 l 2 l_{2} l2范数平方为正则项。假设 ξ i \xi_{i} ξi是高斯白噪声,则带 l 2 l_{2} l2范数平方正则项的线性回归模型实际上是在求解如下问题
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 + u ∣ ∣ x ∣ ∣ 2 2 \mathop{min}\limits_{x\in R^{n}}\frac{1}{2}||Ax-b||^{2}_{2}+u||x||^{2}_{2} x∈Rnmin21∣∣Ax−b∣∣22+u∣∣x∣∣22
由于正则项存在,该问题的目标函数时强凸函数,解的性质得到改善。在岭回归问题中,正则项 ∣ ∣ x ∣ ∣ 2 2 ||x||^{2}_{2} ∣∣x∣∣22的作用实际上是对范数较大的 x x x进行惩罚,因此另一种常见的变形是给定参数 σ > 0 \sigma>0 σ>0,求解
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 , s . t . ∣ ∣ x ∣ ∣ 2 2 ≤ σ \mathop{min}\limits_{x\in R^{n}}\frac{1}{2}||Ax-b||^{2}_{2},\quad s.t.\quad ||x||^{2}_{2}\leq\sigma x∈Rnmin21∣∣Ax−b∣∣22,s.t.∣∣x∣∣22≤σ
②:LASSO问题及其变形
如果希望得到的解 x x x是稀疏的,那么可以考虑添加 l 1 l_{1} l1范数为正则项,对应的正则化问题为LASSO问题,即
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 + u ∣ ∣ x ∣ ∣ 1 \mathop{min}\limits_{x\in R^{n}}\frac{1}{2}||Ax-b||^{2}_{2}+u||x||_{1} x∈Rnmin21∣∣Ax−b∣∣22+u∣∣x∣∣1
其中 u > 0 u>0 u>0为已知的实数, x x x是待估计的参数。LASSO问题通过惩罚参数的 l 1 l_{1} l1范数来控制解的稀疏性,如果 x x x是稀疏的,那么预测值 b i b_{i} bi只和 a i a_{i} ai的部分元素相关。因此,数据点原有的 n n n个特征中,对预测起作用的特征对应于 x x x的分量不为0,从而LASSO模型起到了特征提取的功能
- 注意:也可以考虑问题, m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 , s . t . ∣ ∣ x ∣ ∣ 1 ≤ σ \mathop{min}\limits_{x\in R^{n}}\frac{1}{2}||Ax-b||^{2}_{2},\quad s.t.\quad ||x||_{1}\leq\sigma x∈Rnmin21∣∣Ax−b∣∣22,s.t.∣∣x∣∣1≤σ
如果 ξ \xi ξ不是高斯白噪声,则需要根据具体类型选择损失函数,比如
- m i n x ∈ R n ∣ ∣ A x − b ∣ ∣ 2 + u ∣ ∣ x ∣ ∣ 1 \mathop{min}\limits_{x\in R^{n}}||Ax-b||_{2}+u||x||_{1} x∈Rnmin∣∣Ax−b∣∣2+u∣∣x∣∣1
- m i n x ∈ R n ∣ ∣ A x − b ∣ ∣ 1 + u ∣ ∣ x ∣ ∣ 1 \mathop{min}\limits_{x\in R^{n}}||Ax-b||_{1}+u||x||_{1} x∈Rnmin∣∣Ax−b∣∣1+u∣∣x∣∣1
如果参数 x x x具有分组稀疏性,即 x x x的分量可以分为 G G G个组,每个组内的参数必须同时为零或同时非零,为此人们提出了分组LASSO模型
如果需要同时保证分组以及单个特征的稀疏性,可以考虑将两种正则项结合起来,即有稀疏分组分组LASSO模型
- 其中 u 1 , u 2 > 0 u_{1}, u_{2} > 0 u1,u2>0为给定的常数
当特征 x x x本身不稀疏但在某种变换下是稀疏的,则需要调整正则项
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 + u ∣ ∣ F x ∣ ∣ 1 \mathop{min}\limits_{x\in R^{n}}\quad \frac{1}{2}||Ax-b||_{2}^{2}+u||Fx||_{1} x∈Rnmin21∣∣Ax−b∣∣22+u∣∣Fx∣∣1
假设 x x x在某线性变换 F ∈ R p × n F\in R^{p×n} F∈Rp×n下是稀疏的,如果要求 x x x相邻点之间的变化是稀疏的,则取 F F F为
实际上 ∣ ∣ F x ∣ ∣ 1 ||Fx||_{1} ∣∣Fx∣∣1还可以与 ∣ ∣ x ∣ ∣ 1 ||x||_{1} ∣∣x∣∣1结合起来,这表示同时对 F x Fx Fx和 x x x提出稀疏性的要求,例如融合LASSO模型(fused-LASSO)
m i n x ∈ R n 1 2 ∣ ∣ A x − b ∣ ∣ 2 2 + u 1 ∣ ∣ x ∣ ∣ 1 + u 2 ∑ i = 2 n ∣ x i − x i − 1 ∣ \mathop{min}\limits_{x\in R^{n}}\quad \frac{1}{2}||Ax-b||_{2}^{2}+u_{1}||x||_{1}+u_{2}\sum\limits_{i=2}^{n}|x_{i}-x_{i-1}| x∈Rnmin21∣∣Ax−b∣∣22+u1∣∣x∣∣1+u2i=2∑n∣xi−xi−1∣
- u 2 ∑ i = 2 n ∣ x i − x i − 1 ∣ u_{2}\sum\limits_{i=2}^{n}|x_{i}-x_{i-1}| u2i=2∑n∣xi−xi−1∣用来控制相邻稀疏之间的平稳度