文本处理算法_关键词提取和文本摘要算法TextRank详解及实战

关键词提取和文本摘要算法TextRank详解及实战

写在前面

最近一直没有更新文章，实在惭愧。伴随着小老弟的职业方向由风控转向了NLP，后面的文章也会集中在NLP领域，希望大家能够继续支持~

导读

本文围绕原理和特点介绍了关键词提取和文本摘要算法TextRank，并给出了实现代码和算法效果。

TextRank主要有关键词提取和文本摘要两个功能，在Jieba分词里也有集成，在介绍TextRank的原理之前，必须介绍下PageRank，理解了PageRank，也就理解了TextRank的精髓。

PageRank

PageRank算法用于解决互联网网页的价值排序问题，对于某个关键词的搜索，往往会有很多网页与之相关，如何对这些网站进行排序然后返回给用户最有”价值“的网站？最直观的，对每个网页进行“打分”，而打分标准至关重要。

PageRank考虑到不同网页之间，一般会通过超链接相连，即用户可以通过A网页中的链接，跳转到B网页，这种互相跳转关系，可以理解为一种“投票”行为，A网页连接到B网页，表示A网页对B网页的认可，即A网页给B网页投了一票。给B网页投票(链接)的越多，B网页的价值也就越大，所以：

公式中，某个网页的价值，是由连接到(进入)这个网页的每个网页的价值和对应的权重决定的。一个网站，如果越多的网站链接到它，说明这个网站越有价值，为什么要加入一个权重呢？公式可以看到，权重是从某个网页链接出去的数量的倒数，数量越多，权重越小，好比是投票，某个人投出的票越多，说明这个人的票越没有含金量。

从公式中可以看到这是一个迭代公式，所以存在“先有鸡还是先有蛋”的问题，对于这个问题，解决办法是给每一个节点一个初始值，一般是1/N，N即N个网页。

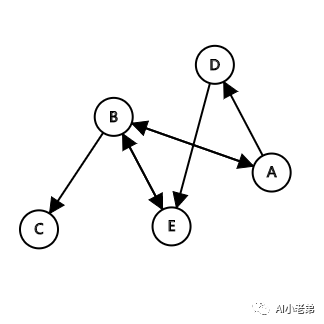
假设现在有5个网页：

……

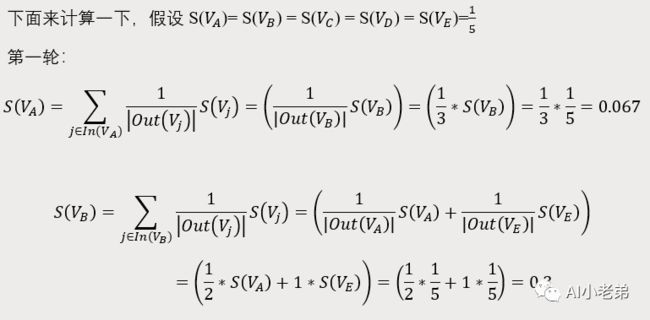
小老弟就不挨着算了，可以看到这样计算是非常麻烦的，同时对于这5个网页之间的关系表示，也非常麻烦，很不优雅，很不数学，所以就要引入一个新的概念-邻接矩阵(Adjacency Matrix)。

首先介绍一个词：图(Graph)。做知识图谱的肯定很了解它，当然，随着相关理论的发展，图论越来越多的出现在了机器学习和深度学习的各个领域，并且取得了很好的效果。

这里就进行简单的介绍，所谓“图”，由节点(node)和边(edge)构成，在这里，节点就是网页，两网页间是否存在边则由两网页是否存在超链接决定。

前面的图中，可以认为是A-E 5个网页构成的图，节点与节点之间存在着边，图中存在箭头，此时的图称为“有向图”。

B到C的箭头表示B网页有到C网页的链接，而A、B之间的箭头表示A、B网页之间相互链接。

这是图的直观展示，如何转化成数学表示呢？就要靠邻接矩阵。

G就是表示上面图的邻接矩阵，第i行第j列为1，表示第i个节点到第j个节点有边，比如第1行第2列，表示节点A到节点B的边。G中的1表示无权重的图，如果是有权图，则这里的1可以替换为相应权重。

有了邻接矩阵，通过标准化，我们可以计算出概率转移矩阵：

第i行表示进入到第i个节点的概率分布，而第j列，表示第j个节点的出节点概率分布。这里突然扯到了概率转移矩阵，实际这是对前面的“投票”打分机制的一种概率抽象，可以这么理解，给到一只猴子和一台电脑，这个猴子随机选择一个网页，然后随机点击网页上的超链接在网页中跳转，一段时间后，猴子在每个网页上停留的概率都会有一个稳定值，这个值就是我们要求的每个网页的“价值”。

我们可以用一个5维列向量S表示5个节点的概率初始值,也就是一个随机向量。

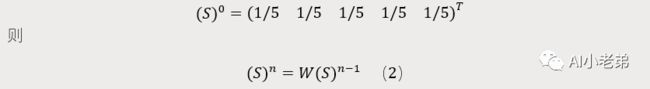
相当于我们对随机向量S反复进行W概率转移过程，补充一点，公式(3)中，概率转移矩阵W左乘随机列向量S，所以W是一个左随机矩阵，也有相反的情况，即概率矩阵右乘随机行向量，那么这个时候就是一个右随机矩阵。

我们利用矩阵运算来进行前面的迭代公式计算：

第一轮：

我们希望得到一个稳定值，于是迭代100轮，

收敛到几乎为0了，这显然是不合理的，为什么呢？实际上，这也是PageRank最初遇到的问题之一，即Dead Ends问题，回到最上面的A-E节点的连接图，可以看到，D节点不存在外链，这种节点，就称为Dead Ends，解决办法呢，就是加入一个阻尼因子：

其实这个d有些类似机器学习中目标函数里的正则项，加入的作用也是让整个计算更平滑一些。

此外，虽然前面说W矩阵是概率转移矩阵，但它并不真正满足概率转移矩阵的定义：

矩阵各元素都是非负的，并且各行(列)元素之和等于1，在一定条件下是互相转移的。

同时，求S的过程，实际是一个马尔科夫收敛过程，而马尔科夫收敛，也需要满足一定的条件，首先必须满足转移矩阵的定义，其次转移矩阵不可约，且非周期。转移矩阵不可约指的是每一个状态都可来自任意的其它状态，也就是任意两个网页都可以通过若干中间网页链接。周期指的是存在一个最小的正整数 k，使得从某状态 i 出发又回到状态 i 的所有路径的长度都是 k 的整数倍，也就是DeadEnds问题，这里由于d的存在，也使得非周期性得到满足。

同样基于公式进行计算，第一轮：

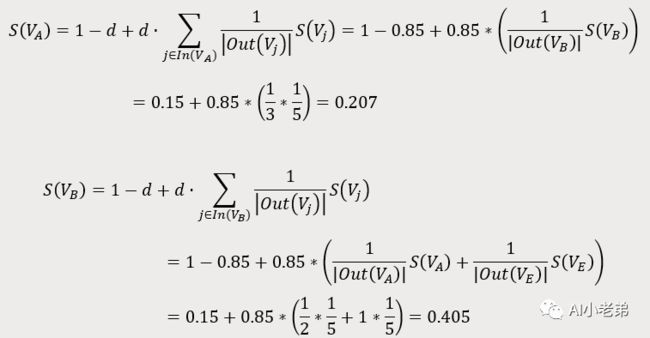
写成矩阵运算，不过这次加入了d，则：

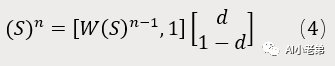
第一轮：

已经收敛了，标准化后：

至此，PageRank的原理和计算过程基本介绍完毕，不难发现，构建“图”，或者说邻接矩阵，是最基础和重要的一步，最终结果也只受邻接矩阵的影响。对于文本来说，TextRank又是如何构建图的呢？这需要结合具体任务去看。

关键词提取任务

在这个任务中，词就是Graph中的节点，而词与词之间的边，则利用“共现”关系来确定。所谓“共现”，就是共同出现，即在一个给定大小的滑动窗口内的词，认为是共同出现的，而这些单词间也就存在着边，举例：

“淡黄的长裙，蓬松的头发

牵着我的手看最新展出的油画”

分词后：

淡黄  长裙  蓬松  头发

牵  我  手  看  最新  展出  油画

给定窗口为2，依次滑动：

淡黄  长裙

长裙  蓬松

蓬松  头发

牵  我

我  手

。。。

则“淡黄”和“长裙”两个节点间存在边：

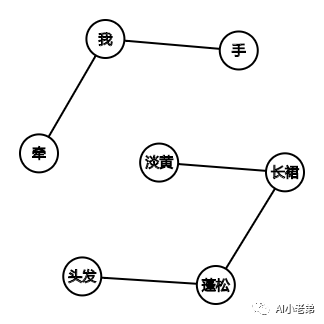
也可以取窗口为3，则“淡黄”不仅和“长裙”存在边，也和“蓬松”存在边。

不难发现，相对于PageRank里的无权有向图，这里建立的是无权无向图，原论文中对于关键词提取任务主要也是构建的无向无权图，对于有向图，论文提到是基于词的前后顺序角度去考虑，即给定窗口，比如对于“长裙”来说，“淡黄”与它之间是入边，而“蓬松”与它之间是出边，但是效果都要比无向图差。

构造好图后，剩下的就是按照PageRank的公式进行迭代计算，论文中有一个公式：

实际上，这个权重，是针对摘要任务中的句子相似度而言的，对于关键词抽取任务，并没有提出新的计算公式，使用的就是(3)式，小老弟在某些博客里看到把这俩公式混为一谈，需要注意。

文本摘要任务

文本摘要任务，也可以理解为“关键句“提取任务，在这个任务中，节点不再是词，而是句子。而句与句之间的联系，也不再使用”共现“来确定，还是利用相似度确定。因此，此时构造的是有权无向图。对于相似度的计算方法，论文中给出了一种：

其中，分母即两个句子的词数取对数后求和，分子是同属于两个句子的词的数量。

当然，也可以使用其他相似度计算方法，比如在有的改进的TextRank方法中，会使用余弦相似度，即先把两个句子分词，词向量化后，利用词向量加和求平均的方式计算句向量，然后再计算两个句子的余弦相似度。

假设我们有A-E五个句子，则构造的邻接矩阵则是：

可以看到，是一个对称矩阵，这是因为两个句子之间不存在方向的关系，这也是无向图的邻接矩阵的特点之一。

同样，也进行标准化处理，实际上，标准化处理后的权重，就是式子(5)中对应的权重。仍然可以利用矩阵计算公式(4)进行迭代计算。

总结

TextRank的论文中测试了很多种方法，结合实际来看，TextRank的优缺点总结如下：

优点：

1)  无监督方式，无需构造数据集训练。

2)  算法原理简单且部署简单。

3)  继承了PageRank的思想，效果相对较好，相对于TF-IDF方法，可以更充分的利用文本元素之间的关系。

缺点：

1)  结果受分词、文本清洗影响较大，即对于某些停用词的保留与否，直接影响最终结果。

2)  虽然与TF-IDF比，不止利用了词频，但是仍然受高频词的影响，因此，需要结合词性和词频进行筛选，以达到更好效果，但词性标注显然又是一个问题。

实战

至此，TextRank介绍完毕，在实操过程中，小老弟发现网上的代码很多是基于networkx包里的pagerank方法进行的计算，与论文公式计算的结果有出入，本着“纸上得来终觉浅“的原则，小老弟动手写了一下TextRank。项目主要结构如下：

-TextRank

--textPro.py : 文本处理，分句分词去停用词，根据词性过滤词。

--textRank.py：实现抽取N个关键词和N个关键句。

--utils.py：共现矩阵的构造，值的计算等。

--const.py：某些常量

运行效果：

原文来自新华网的新闻，见下图，可以看到效果还是蛮不错的。

至此，全文结束。

获取代码

关注公众号，发送“textrank”，获取相关代码和论文。也可至GitHub：https://github.com/abner-wong/textrank

谢谢您的阅读

感觉还行？请点下“在看”，谢谢您！