论文解读（源码）：求解柔性作业车间调度问题（FJSP）的多动作（multi-action）深度强化学习框架

获取更多资讯，赶快关注上面的公众号吧！

今天给大家带来一篇由西南交通大学于2022年发表在《Expert Systems With Applications》上的一篇文章《A multi-action deep reinforcement learning framework for flexible Job-shop scheduling problem》，这篇文章最大的创新就是针对柔性作业车间调度问题，如何通过强化学习解决多决策问题（一般强化学习每次只能输出一个动作，而在FJSP中存在两个决策点）。原先我的处理方式是将枚举出工序和机床所有可能的组合方式，构成动作空间（基于端到端深度强化学习的柔性作业车间调度问题研究），但我认为这并不是一种很聪明的做法，所以我也学习一下这篇文章是如何处理的。此外，本文是将析取图直接输入到网络中，采用图神经网络进行训练，我之前（基于深度强化学习的自适应作业车间调度问题研究）虽然也采用了析取图模型，并使用图像作为状态，采用卷积神经网络训练，但是个人感觉输入的仍然是部分信息，可能无法完全反映调度状态，图神经网络可能是一种更加适合的方法。作者也开源了代码，公众号（智能制造与智能调度）回复“多动作”下载原文和源码。

摘要：本文提出了一种端到端深度强化学习框架，基于图神经网络自动学习柔性作业车间调度问题的求解策略。在FJSP环境中，强化学习代理需要在每一时间步，将工件工序安排到可选机床集合中的一台上。这意味着代理需要同时控制多个动作（工件排序动作和机床选择动作）。这样一个具有多个动作的问题可以建模为多马尔科夫决策过程（MMDP）。为了解决MMDP，作者提出了一种多指针图网络（MPGN）架构，通过多近端策略优化（MPPO）来学习两个子策略（分别对应两种动作），包括工件工序动作策略和机床动作策略，从而将工件工序分配到机床。MPGN架构包括两个编码器-解码器组件，分别定义了工件工序动作策略和机床动作策略，以预测不同工序和机床的概率分布。引入析取图模型表达FJSP，使用图神经网络嵌入调度过程中出现的局部状态。计算结果表明代理可以学习得到高质量的分派策略，并在求解质量上优于启发式分派规则，在运行时间上优于元启发式算法。而且，在随机和标准案例上的结果表明学习到的策略在现实案例和更大规模案例（多大达2000工序）上具有很好的泛化性。

FJSP

柔性作业车间调度问题中，所谓的柔性是相对于一般的作业车间调度问题（JSP）的，是指机床的柔性。JSP中有多个工件，每个工件又有若干工序，每道工序都有提前已知的固定机床，只需要确定所有工序的顺序（工序排序策略）即可。而在FJSP中，每道工序可以有多台机床可用，事先并不知道需要分配到哪台机床，因此在FJSP中除了需要确定工序的顺序，还需要为每道工序选定机床（机床选择策略）。所以JSP实际上是FJSP所有工序的可选机床都只有一台的一种特例。在实际车间生产环境中，为了提高产能或避免机床故障导致停工，往往同一种类型或功能的机床会有多台，因而FJSP是实际中非常常见的一种车间调度问题。

FJSP数学模型（参考了张国辉老师的博士论文《柔性作业车间调度方法研究》）如下：

传统方法

目前已经提出了很多近似算法来求解FJSP问题，包括启发式、元启发式和机器学习技术。相比较于精确算法，近似算法可以在求解效率和求解质量上实现较好的均衡。特别是群体智能（SI）和进化算法（EA），例如遗传（GA）（进化计算-遗传算法-入门级最好教程）、粒子群（PSO）（群体智能之粒子群优化（PSO））、蚁群优化（ACO）（群体智能优化算法之蚁群优化算法(ACO)）、人工蜂群(ABC)（群体智能之人工蜂群算法及其改进(ABC)）等，在求解FJSP时都表现出了较强的实力。

但是，SI和EA在实时重调度环境下就显得不太适用，大量的迭代优化仍然会让算法有很大的时间代价；启发式方法（分派规则）相比较于数学规划和元启发式算法，计算复杂度低且实现简单，设计有效的规则却需要一定的先验知识和大量的试错，很难保证局部最优。

如何又快又好地获得调度解，是各种算法一直追求的目标，而强化学习的泛化作用可以将学习时间放在离线，在线应用时大大提升了求解效率，所以近年来强化学习求解车间调度问题成为一种流行（100篇文献-万字总结 || 强化学习求解车间调度
、30篇强化学习求解车间调度文章（中文）大全）。

创新点

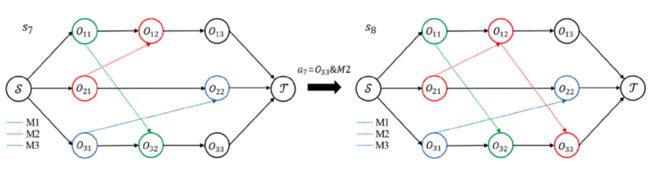
一般的强化学习只有一个动作空间，代理每次和环境交互时从动作空间中选择一个动作。但是在FJSP中有两类决策（工序排序和机床选择），所以一般的强化学习是无法直接使用的。作者针对FJSP专门设计了一种分层多动作空间，包括工件工序动作空间和机床动作空间，这两个空间并不是平行关系而是分层关系，每一时间步，代理先从工序动作空间中选择工序，然后再从机床动作空间中为其选择合适的机床，如下图所示。

作者提出了一种新颖的端到端无模型深度强化学习框架来求解FJSP，该框架可以直接应用于任意FJSP场景，而无需事先对环境进行建模，也就是说，无需对马尔科夫决策过程的转移概率分布（和奖励函数）进行显式定义，同时该框架也不受问题规模的限制，主要创新点如下：

• 引入了FJSP多动作空间的马尔可夫决策过程表达。为解决FJSP问题，给出了引入的多马尔可夫决策过程(mmdp)中的状态、动作和奖励的定义。在此基础上，引入了FJSP的析取图表示，并利用图神经网络嵌入局部状态；
• 设计了一种多指针图网络(MPGN)架构来解决所提出的mmdp问题。MPGN由两个编码器-解码器组件组成，用于定义作业工序动作策略和机床动作策略，分别预测不同工序或机器的概率分布。因此，MPGN可以由小规模问题训练，并泛化到大规模问题；
• 在训练阶段，提出一种多近端策略的算法(multi-PPO)来学习两个子策略，包括工件工序作动作策略和机床动作策略。在标准案例上的计算实验证明了该框架的泛化性能。

强化学习原理

关于强化学习的基本原理可以参看以下往期文章：

• 第一章 强化学习及OpenAI Gym介绍-强化学习理论学习与代码实现（强化学习导论第二版）
• 第二章 马尔科夫决策过程和贝尔曼等式-强化学习理论学习与代码实现（强化学习导论第二版）
• 第三章 动态规划-基于模型的RL-强化学习理论学习与代码实现（强化学习导论第二版）
• 第四章 蒙特卡洛方法-强化学习理论学习与代码实现（强化学习导论第二版）
• 第五章 基于时序差分和Q学习的无模型预测与控制-强化学习理论学习与代码实现（强化学习导论第二版）
• 第六章 函数逼近-强化学习理论学习与代码实现（强化学习导论第二版）
• 第七章 深度强化学习-深度Q网络系列1（Deep Q-Networks，DQN）
• 第八章 深度强化学习-Nature深度Q网络(Nature DQN)
• 第九章 深度强化学习-Double DQN
• 第十章 深度强化学习-Prioritized Replay DQN
• 第十一章 策略梯度（Policy Gradient）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十二章 演员评论家（Actor-Critic）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十三章 确定性策略梯度（Deterministic Policy Gradient Algorithms，DPG）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十四章 深度确定性策略梯度（Deep Deterministic Policy Gradient Algorithms，DDPG）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十五章 第十五章 异步A3C(Asynchronous Advantage Actor-Critic，A3C)-强化学习理论学习与代码实现（强化学习导论第二版）

析取图模型

析取图模型在我之前的文章中也有详细介绍：

• 车间调度建模系列3|复杂车间调度问题解的表示
• 车间调度建模系列4|扩展析取图之工序相关性
• 车间调度建模系列5|扩展析取图之工序间物流周转时间
• 车间调度建模系列6|扩展析取图之顺序不依赖准备时间
• 车间调度建模系列7|扩展析取图之基于设备偏好的三维析取图模型
• 车间调度建模系列8|扩展析取图之基于时间片段的赋时三维析取图模型
• 车间调度建模系列9|复杂车间调度问题建模实例

方法详解

问题设置

在每一时间步，代理为每道就绪工序输出一个优先级，并根据采样（按概率大小）或贪婪解码策略（选择概率最大的）选择其中一个进行分派，然后代理再为选择的工序计算每台可选机床的优先级，根据采样或贪婪解码策略选择其中一个，因此代理需要同时控制两个动作，这种多动作（或称多任务）强化学习可建模为马尔科夫决策过程$(\mathcal{S},\mathcal{A},P,r,\gamma )$，动作集$\mathcal{A}={\mathcal{A}}_o\times {\mathcal{A}}_m$是二维的，其中$\mathscr{A}_o $是就绪工序子动作集，$ \mathscr{A}_m$是可选机床子动作集。这个与多动作空间相结合的MDP称为多个MDP (MMDP)。

1 状态：时间步$t$的全局状态$s_t$由局部状态$s_t^o$和$s_t^m$组成。局部状态$s_t^o$是析取图$G_t=\left(\mathcal{O},\mathcal{C}\cup {\mathcal{D}}_t^0,{\mathcal{D}}_t\right)$，其中${\mathcal{D}}_t^0\subseteq \mathcal{D}$是$t$时刻为止已经确定方向的析取弧，${\mathcal{D}}_t\subseteq \mathcal{D}$则是剩余的析取弧集合。每个节点$O_{ij}\in \mathcal{O}$包括两个特征$\left[L{B}_t\left(O_{ij}\right),I_t\left(O_{ij}\right)\right],i\in \left\{1,\cdots ,n\right\},j\in \left\{1,\cdots ,n_i\right\}$，其中$L{B}_t\left(O_{ij}\right)$是已调度工序$O_{ij}$的完成时间，或是未调度工序的估计最早完成时间$L{B}_t\left(O_{i,j-1}\right)+\min \left(p_{ijk},k\in {\mathcal{M}}_{ij}\right)$。$I_t\left(O_{ij}\right)$为是否已调度标志，1表示已调度，0表示未调度。$s_t^m$包含所有机床的状态，每个机床状态包含二维特征$\left[T_t\left(M_k\right),p_{ijk}\right],k\in \{1,\cdots ,m\}$，其中$T_t\left(M_k\right)$是机床时间步$t$之前的完成时间，而且如果机床$M_k$可用于加工工序$O_{ij}$，那么$ p_{i j k}$为工序在机床上的加工时间，而如果不兼容，则$ p_{i j k}$为在可用于当前工序的所有机床上的加工时间的平均值$\frac{1}{|K|}\sum_k p_{ijk},k\in K$。

2 动作：时间步$t$的动作包括工件工序动作$a_0\in {\mathcal{A}}_o$和机床动作$a_m\in {\mathcal{A}}_m$。${\mathcal{A}}_o$是就绪工序集合，${\mathcal{A}}_m$是针对动作$a_0$的可选机床集合。工件工序动作空间${\mathcal{A}}_o$取决于未完工件的交集，机床动作空间${\mathcal{A}}_m$取决于选定工序的可选机床数量。

3 转移：时间步$t$，代理采样一道工序$a_0$并为其选择一台机床，然后，基于当前工件工序动作和机床动作更新析取弧的方向，新的析取图就作为新的局部状态$s_{t+1}^o$，然后机床完成时间$T_{t+1}\left(M_k\right)$和工序$a_0$的加工时间$p_{ijk}$更新为新的局部状态$s_{m+1}^o$。

4 奖励：目标是最小化makespan，为此比较了连续两个时间步两个部分解之间的差别$d_t=C\left(s_{t+1}\right)-C\left(s_t\right)$，其中$C\left(s_t\right)={\max }_{ij}\left\{L{B}_t\left(O_{ij}\right)\right\}$为$L{B}_t\left(O_{ij}\right)$的makespan。然后，设置奖励为$r\left(s_t,a_o,a_m\right)=-d_t$，那么累积奖励就是所有工序调度完成后最终makespan的负数。

5 策略：策略${\pi }_{\Theta }\left(a_0,a_m\mid s\right)$包括两个所及子策略${\pi }_{{\theta }_o}\left(a_0\mid s\right)$和${\pi }_{{\theta }_m}\left(a_m\mid s,a_o\right)$，其中${\theta }_o$和${\theta }_m$分别是工件工序策略和机床策略的参数。策略${\pi }_{\Theta }\left(a_0,a_m\mid s\right)$根据工件工序动作空间和机床动作空间的概率分布分别选择工件工序动作和机床动作。

子策略参数化

为了处理具有多动作空间的FJSP，作者提出了一个多指针图网络(MPGN)，用于参数化负责各自动作选择的两个子策略，如下图所示。

工件工序编码（图嵌入）

上述mmdp中的析取图提供了包含数值和结构信息的调度状态的完整视图，如顺序约束、每台机床上的加工顺序、每道工序的可用机床集以及每道工序可用机床的加工兼时间。提取析取图中包含的所有状态信息是实现有效调度性能的关键，可以利用图神经网络(GNN)来嵌入复杂的图状态。

具体就是采用了图同构网络（ Graph Isomorphism Network,GIN）来编码析取图即局部状态$s_t^o$，在时间步$t$，局部状态$s_t^o$根据析取图来定义，其中每个节点通过一个L层GIN进行编码，GIN的每一层结构如下：${\mathbf{h}}_{v,t}^{(l)}$是第$l$层GIN中节点$v$嵌入，${\mathbf{h}}_{v,t}^{(0)}$则为输入的主要特征，$ML{P}_{{\theta }_l}^{(l)}$是第$l$层的多层感知器，${\theta }_l$是该层的参数，\epsilon^{(l)}是可学习参数。

$${\mathbf{h}}_{v,t}^{(l)}=ML{P}_{{\theta }_l}^{(l)}\left(\left(1+{ϵ}^{(l)}\right)\bullet {\mathbf{h}}_{v,t}^{(l-1)}+\sum _{u\in \mathcal{N}(v)}{\mathbf{h}}_{u,t}^{(l-1)}\right),l\in \{1,\cdots ,L\};v,t\in \{1,\cdots ,|\mathcal{O}|\}$$

析取图$G_t$是一种具有有向弧和无向弧的混合图，在将其输入到GIN之前，需要进行预处理以执行$G_t$的转移，具体来说，就是将一条无向弧替换为两条方向相反、连接相同节点的有向弧，如下图所示。

但是这种策略使得图过于密集，GIN无法有效地处理。作者采用“加弧方案”，忽略初始状态下的无向析取弧，以降低计算复杂度，如下图所示。

机床编码器（节点嵌入）

在机器的状态信息中不存在图结构，机床状态信息中每个节点表示每台机床的主要特征，节点之间不会通过有向弧或无向弧连接。因此，采用全连接层对局部状态进行编码。

解码器（动作选择）

通过每一时间步$t\in \{1,\cdots ,|O|\}$的解码就可以顺序构造完整的调度，其中$|O|$为总工序数。每一时间步，工件解码器基于局部状态$s_t^o$选择一个工件工序动作$a_t^o$，机床解码器基于局部状态$s_t^m$选择一个机床动作$a_t^m$，从而构成一个完整的动作$a_t=(a_t^o,a_t^m)$。

这两种解码器基于MLP层，具有相同的网络结构，但不共享参数。在解码中，每个解码器分别计算工件工序动作空间或机床动作空间上的概率分布。首先，两个解码器会用于输出工件工序动作分数$c_{t,v}^o$和机床动作分数$c_{t,k}^m$。

$$c_{t,v}^o=ML{P}_{{\theta }_{{\pi }_o}}\left({\mathbf{h}}_{v,t}^{(L)}\Vert {\mathbf{h}}_{\mathcal{G}}^t\Vert {\mathbf{u}}^t\right),v\in \{1,\cdots ,|\mathcal{O}|\}$$

$$c_{t,k}^m=ML{P}_{{\theta }_{{\pi }_m}}\left({\mathbf{h}}_k^t\Vert {\mathbf{h}}_{\mathcal{S}}^t\Vert {\mathbf{u}}^t\right),k\in \{1,\cdots ,|\mathcal{M}|\},$$

为了避免分派已调度的或违反顺序的工序，同时也保证选择可用于加工工序的机床，作者采用了掩码机制，其实就是一些状态判断，具体来说就是已调度或违反约束的工序所对应的分数被掩码处理成$-\infty$，从而保证不会被选到。

最后，将工件工序动作分数和机床动作分数进行Softmax归一化，其实就是变成概率：
$$p_i\left(a_t^o\right)=\frac{e^{c_{t,i}^o}}{{\sum }_v{e}^{c_{t,v}^o}},$$

$$p_j\left(a_t^m\right)=\frac{e^{c_{t,j}^m}}{{\sum }_k{e}^{c_{t,k}^m}},$$
那么就可以根据以上概率，应用采样策略或贪婪解码策略来预测工件工序动作和机床动作。

多近端策略优化

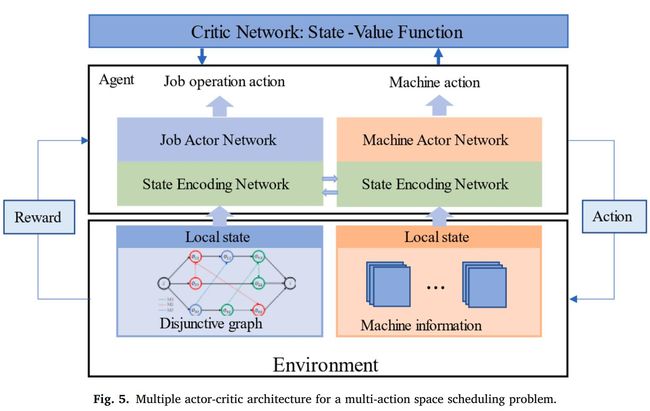
为了训练多动作，作者采用了多actor-critic（演员-评论家）架构，使用多PPO作为学习两个子策略的优化方法，多PPO具有两个动作网络，就是上面描述的工件工序和机床编码器-解码器，但是评价网络是一个。训练过程如下图所示。

优化算法伪代码如下：

实验结果

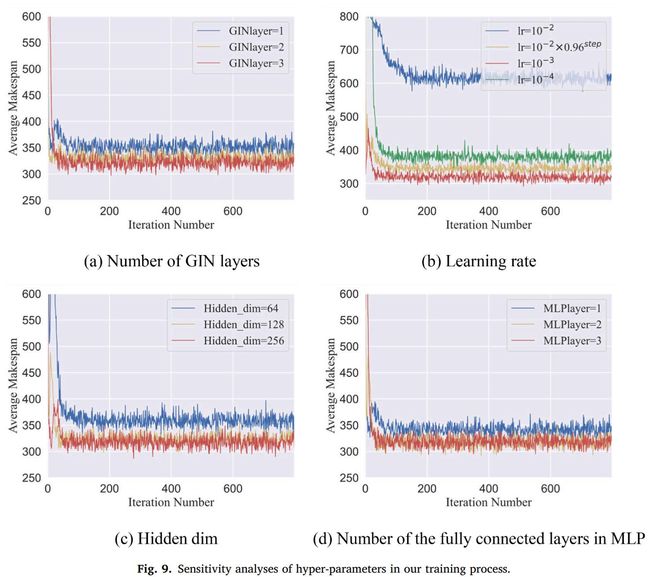
数据集：提出的框架在各种大小的FJSP案例上进行评估，训练集12800个案例，验证集128个案例，测试集也是128个案例，这些案例都是随机生成的。训练和验证过程主要是在中小规模案例上进行训练和验证的，并直接在更大规模的案例上进行测试。同时在标准案例上也进行了测试。

超参数：超参数固定，除了不同规模的问题使用了不同的批量。

随机案例结果

可以看出，本文提出的方法相比较于规则，质量更优且稳定，且比求解器效率高的多。

作者还评估了泛化性能，可以看出测试结果仍然优于规则，

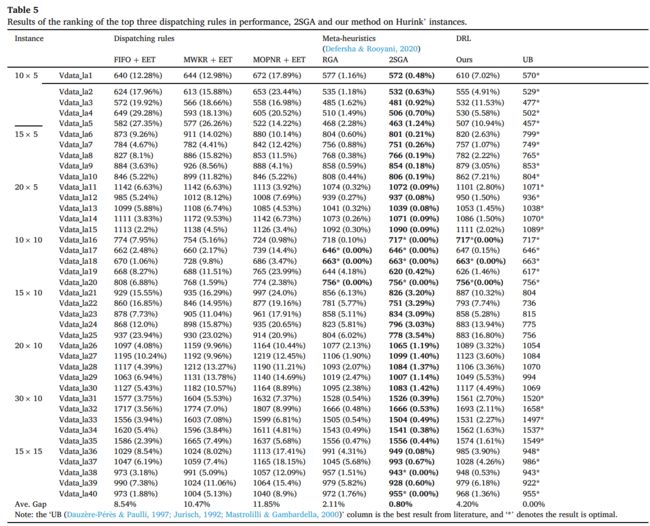
标准案例结果

作者选用了Hurink和Behnke案例，可以看出，结果仍然比规则好，虽然比元启发式算法差一些，但是求解时间少很多。

结论

本文引入一个基于端到端DRL框架，学习一种最小化FJSP最大完成时间的调度策略。我们为FJSP提出了一个多mdps公式，并引入了状态、操作和奖励的新表示，以解决复杂的调度问题。采用了FJSP的析取图表示来表示局部状态，并使用图神经网络来嵌入局部状态。然后设计了一个神经网络来学习两个策略，一个是工件工序策略，一个是机床策略。这两种策略分别用于预测工件工序和机床的概率分布。此外，经过训练的策略网络能够处理在工件、工序和机床方面具有不同规模的未知案例。同时，设计了一种多近端策略优化算法来训练神经网络。为了评估所提框架的泛化性，通过随机生成实例训练策略网络，并在标准案例上进行测试，同时通过小规模实例训练策略网络，在大规模基准上进行测试。在随机案例和标准案例测试上的实验表明，该方法的性能明显优于现有调度规则（又快又好）。