GCN论文阅读与代码梳理（5）——STSGCN
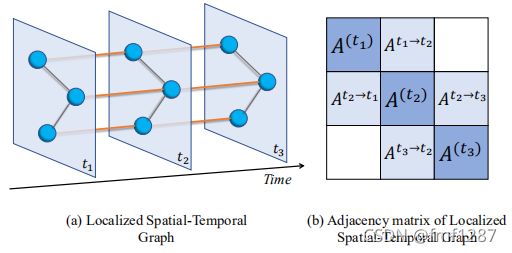
时空影响图如下：
-
棕色箭头：每个节点都在同一时间步影响其相邻节点。
-
蓝色箭头：每个节点都在下一时间步影响自身。
-
绿色箭头：由于同步的时间相关性，每个节点可以再下一时间步影响其相邻节点。
提出STSGCN的原因：
-
DCRNN、STGCN、ASTGCN提出了捕获时间和空间依赖关系的独立模块，但本文相信如果同时捕获时空关联将会更有效。
-
时空网络在时空维度上表现出异质性，即不同地点不同时间的交通流量会呈现不同的pattern，但之前的研究在不同的时间共享同一个模块。
本文的贡献有：
-
提出了一个时空图卷积模块同时捕获局部时空相关性信息。
-
构建了一个多模块层捕获长期时空图的异质性。
-
在四个真实数据上表现优异。
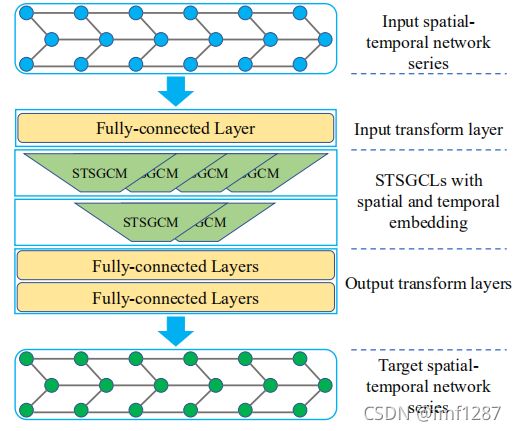
STSGCN的架构如下：
其核心思想如下：
1）在上一个和下一个步骤将每个节点与其自身连接，以构造局部时空图。
2）使用时空同步图卷积模块捕获局部时空相关性。
3）部署多个模块以对时空网络系列中的异构性进行建模。
具体的：
-
局部时空图构建
表示构造在三个连续空间图上的局域时空图的邻接矩阵，如下图。
为空间图在时间步i的邻接矩阵，
为节点在时间步i与时间步j与自身的联系。
相应代码如下：
def construct_adj(A, steps):
'''
construct a bigger adjacency matrix using the given matrix
Parameters
----------
A: np.ndarray, adjacency matrix, shape is (N, N)
steps: how many times of the does the new adj mx bigger than A
Returns
----------
new adjacency matrix: csr_matrix, shape is (N * steps, N * steps)
'''
N = len(A)
adj = np.zeros([N * steps] * 2)
for i in range(steps):
adj[i * N: (i + 1) * N, i * N: (i + 1) * N] = A
for i in range(N):
for k in range(steps - 1):
adj[k * N + i, (k + 1) * N + i] = 1
adj[(k + 1) * N + i, k * N + i] = 1
for i in range(len(adj)):
adj[i, i] = 1
return adj-
时空embedding
其中，
为时空网络序列，
为一个可学习的时间嵌入矩阵，
为一个可学习的空间嵌入矩阵。
相应代码如下：
def position_embedding(data,
input_length, num_of_vertices, embedding_size,
temporal=True, spatial=True,
init=mx.init.Xavier(magnitude=0.0003), prefix=""):
'''
Parameters
----------
data: mx.sym.var, shape is (B, T, N, C)
input_length: int, length of time series, T
num_of_vertices: int, N
embedding_size: int, C
temporal, spatial: bool, whether equip this type of embeddings
init: mx.initializer.Initializer
prefix: str
Returns
----------
data: output shape is (B, T, N, C)
'''
temporal_emb = None
spatial_emb = None
if temporal:
# shape is (1, T, 1, C)
temporal_emb = mx.sym.var(
"{}_t_emb".format(prefix),
shape=(1, input_length, 1, embedding_size),
init=init
)
if spatial:
# shape is (1, 1, N, C)
spatial_emb = mx.sym.var(
"{}_v_emb".format(prefix),
shape=(1, 1, num_of_vertices, embedding_size),
init=init
)
if temporal_emb is not None:
data = mx.sym.broadcast_add(data, temporal_emb)
if spatial_emb is not None:
data = mx.sym.broadcast_add(data, spatial_emb)
return data-
时空同步图形卷积模块(STSGCM)
图卷积层可被描述为
相应代码如下：
def gcn_operation(data, adj,
num_of_filter, num_of_features, num_of_vertices,
activation, prefix=""):
'''
graph convolutional operation, a simple GCN we defined in paper
Parameters
----------
data: mx.sym.var, shape is (3N, B, C)
adj: mx.sym.var, shape is (3N, 3N)
num_of_filter: int, C'
num_of_features: int, C
num_of_vertices: int, N
activation: str, {'GLU', 'relu'}
prefix: str
Returns
----------
output shape is (3N, B, C')
'''
assert activation in {'GLU', 'relu'}
# shape is (3N, B, C)
data = mx.sym.dot(adj, data)
if activation == 'GLU':
# shape is (3N, B, 2C')
data = mx.sym.FullyConnected(
data,
flatten=False,
num_hidden=2 * num_of_filter
)
# shape is (3N, B, C'), (3N, B, C')
lhs, rhs = mx.sym.split(data, num_outputs=2, axis=2)
# shape is (3N, B, C')
return lhs * mx.sym.sigmoid(rhs)
elif activation == 'relu':
# shape is (3N, B, C')
return mx.sym.Activation(
mx.sym.FullyConnected(
data,
flatten=False,
num_hidden=num_of_filter
), activation
)STSGCM的结构如下：
在AGG中包含两个操作：1）聚合，
；2）裁剪，删除每个节点的上一时刻和下一时刻特征，因为图卷积已经保留了上一时刻和下一时刻的信息，多个STSGCM叠加的话会有许多冗余信息。
相应代码如下：
# 裁剪
need_concat = [
mx.sym.expand_dims(
mx.sym.slice(
i,
begin=(num_of_vertices, None, None),
end=(2 * num_of_vertices, None, None)
), 0
) for i in need_concat
]
# 聚合
mx.sym.max(mx.sym.concat(*need_concat, dim=0), axis=0)-
时空同步图卷积层(STSGCL)
包含T-2个STSGCM，输出为![M=[M_1,M_2,...,M_{T-2}] \in R^{(T-2)\times N\times C_{out}}](http://img.e-com-net.com/image/info8/7d8d44439dcc44639b27440d16e3f3e4.gif){kind=small}
另外，利用一个mask矩阵调整聚合权值，使聚合更合理：
相应代码如下：
mask = mx.sym.var("{}_mask".format(prefix),shape=(3 * num_of_vertices, 3 * num_of_vertices), init=mask_init_value)
adj = mask * adj输入利用全连接层提升了网络的表征能力。
输出利用两层全连接层生成预测值：第i时间步的预测值为
data = mx.sym.FullyConnected(data,flatten=False,num_hidden=predict_length)