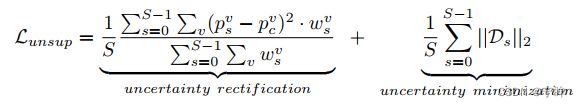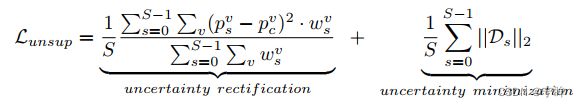半监督3D医学图像分割（三）：URPC

Efficient Semi-supervised Gross Target Volume of Nasopharyngeal Carcinoma Segmentation via Uncertainty Rectified Pyramid Consistency

深度学习归根结底是数据驱动的，模型训练的好坏依赖于数据集。在医学图像分割领域，即使是像nn-UNet那样强大的训练框架，也受限于数据集的大小。相比自然图像，医学图像的标注代价更加昂贵，相反，无标注的图像有很多。半监督学习的目的就是将无标注的数据利用起来，达到比单独用有标注数据集更好的效果。

前两篇博客介绍的方法，都是student-teacher双路模型，URPC是单路模型。TS模型是在学生网络和教师网络之间做一致性损失，URPC则是多级特征内部做一致性损失，相比TS架构的计算量和显存大大降低。

网络结构

Overview of the proposed Uncertainty Rectified Pyramid Consistency framework

• 以U-Net为基础（Backbone），E是编码器（Encoder），D是解码器（Decoder）
• p0,p1,p2,ps是解码器不同层的预测结果，通过上采样统一尺寸
• 绿色和红色箭头分别代表分割损失（有标注）和一致性损失（无标注）

论文在U-Net的解码器增加了一个金字塔预测结构，叫做PPNet。PPNet输出多尺度的预测结果，和标签计算分割损失，与Rectified后的特征做一致性损失。同时引入了深监督，一致性损失，不确定性抑制的概念。
$$[p_0^{\prime },p_1^{\prime },p_2^{\prime },p_s^{\prime }]=[f(x|D_0),f(x|D_1),f(x|D_2)，f(x|D_3)]$$

• p’是解码器不同层的输出，不同特征的分辨率和通道数是不一样的

$$[p_0,p_1,p_2,p_s]=[g(p_0^{\prime }),g(p_1^{\prime }),g(p_2^{\prime }),g(p_s^{\prime })]$$

• g由上采样模块、 1x1x1的卷积层和softmax层组成
• p是概率图（C x H x W x D），此时分辨率和通道数都是一样的

损失函数

1.分割损失

医学图像分割任务中常用的交叉熵和dice损失，s个预测结果分别与标签计算损失，然后取平均
$$L_{sup}=\frac{1}{S}\sum _{s=0}^{S-1}\frac{L_{dice}(p_s,y_i)+L_{ce}(p_s,y_i)}{2}$$
2.无监督损失

为了有效利用无标注数据，URPC利用多尺度特征计算一致性损失，从而引入了正则化。具体而言，设计了金字塔一致性损失最小化不同尺度预测之间的差异。首先，对这些预测结果求平均：
$$p_c=\frac{1}{S}\sum _{s=0}^{S-1}{p}_s$$
金字塔一致性损失定义为：
$$L_{pyc}=\frac{1}{S}\sum _{s=0}^{S-1}||p_s-p_c|{|}_2$$
ps是不同尺度的预测结果，pc是均值，ps与pc计算MSE

3.不确定性修正

计算不确定度

不同尺度的特征分辨率不同，如果输入的原图是 H x W x D，上采样四次，则p0~p3的分辨率为 H x W x D，H/2 x W/2 x D/2，H/4 x W/4 x D/4，H/8 x W/8 x D/8。在U-Net网络中，分辨率越低的特征图，通道数越多，语义特征越高级，捕获的低频信息越多。反之，分辨率越高的特征，包含的高频信息越多。由于不同特征的频率信息不同，直接上采样后计算一致性可能存在问题，比如细节信息的丢失。

与上一篇博客提到的UA-MT不同，URPC只需要一次前向传播，能够高效的计算不确定度，用的是KL散度计算预测结果和平均预测结果之间的差异。
$$D_s\approx \sum _{j=0}^C{p}_s^j\cdot log\frac{p_s^j}{p_c^j}$$

• C是分割类别，psj是ps的第j个通道，pcj是pc的第j个通道
• Ds是ps和pc之间的KL散度，用来表示不确定度，形状是 C x H x W x D
• pc可以认为是多尺度预测结果的中心，Ds越大代表离中心越远，不确定性越高

不确定性修正

根据不确定度对上文提到的金字塔一致性损失做了修正，
$${\omega }_s^v=e^{-D_s^v}$$

• psv和pcv分别表示ps和pc在体素v处的概率向量
• 上式第一项是修正后的金字塔一致性损失，第二项有点像正则化，用来降低不确定性
• wsv和Dsv是当前体素的权重和不确定度，根据公式，不确定度越高的区域，分配的权重越低

4.损失函数

URPC在有标注图像上的分割损失和无标注图像上的一致性损失，用一个公式表示
$$L_{total}=L_{sup}+\lambda \cdot L_{unsup}$$

$$\lambda (t)={\omega }_{max}\cdot e^{-5(1-\frac{t}{t_{max}}{)}^2}$$

• Lsup和Lunsup对应有监督损失和无监督损失
• λ是无监督损失的权重，在训练过程中逐渐增加，防止网络训练前期被无意义的目标影响

代码解读

网络就是深监督的U-Net，另外添加4个Dropout层增加了多尺度特征的随机性

class unet_3D_dv_semi(nn.Module):
    def __init__(self, feature_scale=4, n_classes=21, is_deconv=True, in_channels=3, is_batchnorm=True):
        super(unet_3D_dv_semi, self).__init__()
        self.is_deconv = is_deconv
        self.in_channels = in_channels
        self.is_batchnorm = is_batchnorm
        self.feature_scale = feature_scale

        filters = [64, 128, 256, 512, 1024]
        filters = [int(x / self.feature_scale) for x in filters]

        # downsampling
        self.conv1 = UnetConv3(self.in_channels, filters[0], self.is_batchnorm, kernel_size=(3, 3, 3), padding_size=(1, 1, 1))
        self.maxpool1 = nn.MaxPool3d(kernel_size=(2, 2, 2))

        self.conv2 = UnetConv3(filters[0], filters[1], self.is_batchnorm, kernel_size=(3, 3, 3), padding_size=(1, 1, 1))
        self.maxpool2 = nn.MaxPool3d(kernel_size=(2, 2, 2))

        self.conv3 = UnetConv3(filters[1], filters[2], self.is_batchnorm, kernel_size=(3, 3, 3), padding_size=(1, 1, 1))
        self.maxpool3 = nn.MaxPool3d(kernel_size=(2, 2, 2))

        self.conv4 = UnetConv3(filters[2], filters[3], self.is_batchnorm, kernel_size=(3, 3, 3), padding_size=(1, 1, 1))
        self.maxpool4 = nn.MaxPool3d(kernel_size=(2, 2, 2))

        self.center = UnetConv3(filters[3], filters[4], self.is_batchnorm, kernel_size=(3, 3, 3), padding_size=(1, 1, 1))

        # upsampling
        self.up_concat4 = UnetUp3_CT(filters[4], filters[3], is_batchnorm)
        self.up_concat3 = UnetUp3_CT(filters[3], filters[2], is_batchnorm)
        self.up_concat2 = UnetUp3_CT(filters[2], filters[1], is_batchnorm)
        self.up_concat1 = UnetUp3_CT(filters[1], filters[0], is_batchnorm)

        # deep supervision
        self.dsv4 = UnetDsv3(in_size=filters[3], out_size=n_classes, scale_factor=8)
        self.dsv3 = UnetDsv3(in_size=filters[2], out_size=n_classes, scale_factor=4)
        self.dsv2 = UnetDsv3(in_size=filters[1], out_size=n_classes, scale_factor=2)
        self.dsv1 = nn.Conv3d(in_channels=filters[0], out_channels=n_classes, kernel_size=1)

        self.dropout1 = nn.Dropout3d(p=0.5)
        self.dropout2 = nn.Dropout3d(p=0.3)
        self.dropout3 = nn.Dropout3d(p=0.2)
        self.dropout4 = nn.Dropout3d(p=0.1)

    def forward(self, inputs):
        conv1 = self.conv1(inputs)
        maxpool1 = self.maxpool1(conv1)

        conv2 = self.conv2(maxpool1)
        maxpool2 = self.maxpool2(conv2)

        conv3 = self.conv3(maxpool2)
        maxpool3 = self.maxpool3(conv3)

        conv4 = self.conv4(maxpool3)
        maxpool4 = self.maxpool4(conv4)

        center = self.center(maxpool4)

        up4 = self.up_concat4(conv4, center)
        up4 = self.dropout1(up4)

        up3 = self.up_concat3(conv3, up4)
        up3 = self.dropout2(up3)

        up2 = self.up_concat2(conv2, up3)
        up2 = self.dropout3(up2)

        up1 = self.up_concat1(conv1, up2)
        up1 = self.dropout4(up1)

        # Deep Supervision
        dsv4 = self.dsv4(up4)
        dsv3 = self.dsv3(up3)
        dsv2 = self.dsv2(up2)
        dsv1 = self.dsv1(up1)

        return dsv1, dsv2, dsv3, dsv4

$$dsv1,dsv2,dsv3,dsv4对应网络图中的p_0,p_1,p_2,p_3$$

---

for epoch_num in tqdm(range(max_epoch), ncols=70):
    for i_batch, sampled_batch in enumerate(trainloader):
        volume_batch, label_batch = sampled_batch['image'], sampled_batch['label']
        volume_batch, label_batch = volume_batch.cuda(), label_batch.cuda()
        unlabeled_volume_batch = volume_batch[labeled_bs:]

        outputs_aux1, outputs_aux2, outputs_aux3, outputs_aux4,  = model(volume_batch)
        outputs_aux1_soft = torch.softmax(outputs_aux1, dim=1)
        outputs_aux2_soft = torch.softmax(outputs_aux2, dim=1)
        outputs_aux3_soft = torch.softmax(outputs_aux3, dim=1)
        outputs_aux4_soft = torch.softmax(outputs_aux4, dim=1)

• outputs_aux1, outputs_aux2, outputs_aux3, outputs_aux4是多尺度的预测结果

---

		loss_ce_aux1 = ce_loss(outputs_aux1[:args.labeled_bs], label_batch[:args.labeled_bs])
        loss_ce_aux2 = ce_loss(outputs_aux2[:args.labeled_bs], label_batch[:args.labeled_bs])
        loss_ce_aux3 = ce_loss(outputs_aux3[:args.labeled_bs], label_batch[:args.labeled_bs])
        loss_ce_aux4 = ce_loss(outputs_aux4[:args.labeled_bs], label_batch[:args.labeled_bs])

        loss_dice_aux1 = dice_loss(outputs_aux1_soft[:args.labeled_bs], label_batch[:args.labeled_bs].unsqueeze(1))
        loss_dice_aux2 = dice_loss(outputs_aux2_soft[:args.labeled_bs], label_batch[:args.labeled_bs].unsqueeze(1))
        loss_dice_aux3 = dice_loss(outputs_aux3_soft[:args.labeled_bs], label_batch[:args.labeled_bs].unsqueeze(1))
        loss_dice_aux4 = dice_loss(outputs_aux4_soft[:args.labeled_bs], label_batch[:args.labeled_bs].unsqueeze(1))

        supervised_loss = (loss_ce_aux1+loss_ce_aux2+loss_ce_aux3+loss_ce_aux4 +
                           loss_dice_aux1+loss_dice_aux2+loss_dice_aux3+loss_dice_aux4)/8

• 对有标注的图像计算分割损失，即常用的交叉熵和dice损失

---

        preds = (outputs_aux1_soft + outputs_aux2_soft+outputs_aux3_soft+outputs_aux4_soft)/4
        variance_aux1 = torch.sum(kl_distance(torch.log(outputs_aux1_soft[args.labeled_bs:]), preds[args.labeled_bs:]), dim=1, keepdim=True)
        exp_variance_aux1 = torch.exp(-variance_aux1)

        variance_aux2 = torch.sum(kl_distance(torch.log(outputs_aux2_soft[args.labeled_bs:]), preds[args.labeled_bs:]), dim=1, keepdim=True)
        exp_variance_aux2 = torch.exp(-variance_aux2)

        variance_aux3 = torch.sum(kl_distance(torch.log(outputs_aux3_soft[args.labeled_bs:]), preds[args.labeled_bs:]), dim=1, keepdim=True)
        exp_variance_aux3 = torch.exp(-variance_aux3)

        variance_aux4 = torch.sum(kl_distance(torch.log(outputs_aux4_soft[args.labeled_bs:]), preds[args.labeled_bs:]), dim=1, keepdim=True)
        exp_variance_aux4 = torch.exp(-variance_aux4)

        consistency_dist_aux1 = (preds[args.labeled_bs:] - outputs_aux1_soft[args.labeled_bs:]) ** 2
        consistency_loss_aux1 = torch.mean(consistency_dist_aux1 * exp_variance_aux1) / (torch.mean(exp_variance_aux1) + 1e-8) + torch.mean(variance_aux1)

        consistency_dist_aux2 = (preds[args.labeled_bs:] - outputs_aux2_soft[args.labeled_bs:]) ** 2
        consistency_loss_aux2 = torch.mean(consistency_dist_aux2 * exp_variance_aux2) / (torch.mean(exp_variance_aux2) + 1e-8) + torch.mean(variance_aux2)

        consistency_dist_aux3 = (preds[args.labeled_bs:] - outputs_aux3_soft[args.labeled_bs:]) ** 2
        consistency_loss_aux3 = torch.mean(consistency_dist_aux3 * exp_variance_aux3) / (torch.mean(exp_variance_aux3) + 1e-8) + torch.mean(variance_aux3)

        consistency_dist_aux4 = (preds[args.labeled_bs:] - outputs_aux4_soft[args.labeled_bs:]) ** 2
        consistency_loss_aux4 = torch.mean(consistency_dist_aux4 * exp_variance_aux4) / (torch.mean(exp_variance_aux4) + 1e-8) + torch.mean(variance_aux4)

        consistency_loss = (consistency_loss_aux1 + consistency_loss_aux2 + consistency_loss_aux3 + consistency_loss_aux4) / 4

• preds对应pc

$$p_c=\frac{1}{S}\sum _{s=0}^{S-1}{p}_s$$

• variance_aux对应Ds

$$D_s\approx \sum _{j=0}^C{p}_s^j\cdot log\frac{p_s^j}{p_c^j}$$

• exp_variance_aux对应wsv

$${\omega }_s^v=e^{-D_s^v}$$

• consistency_loss对应无监督损失

---

        consistency_weight = get_current_consistency_weight(iter_num//150)
        loss = supervised_loss + consistency_weight * consistency_loss

• consistency_weight对应λ，w_max=0.1，随iteration逐渐增加到0.1

$$\lambda (t)={\omega }_{max}\cdot e^{-5(1-\frac{t}{t_{max}}{)}^2}$$

---

其余代码细节见LASeg: 2018 Left Atrium Segmentation (MRI)中的train_URPC.py

实验结果

论文实验

原论文是在鼻咽癌核磁数据集上做的实验

NPC数据集消融实验（18例有标签，162例无标签，10%）

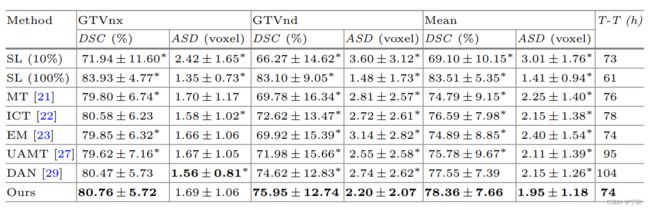
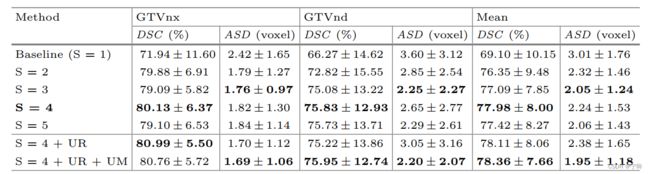
• S是多尺度特征的数量，GTVnx和GTVnd是分割的不同区域，DSC是dice系数，ASD是平均表面距离
• S=4时，分割精度最高。S=3时效果也不错，看的出来，继续增加S提升不大，反而会增加网络参数和计算量
• UR（uncertainty rectification）是不确定性修正，UM（uncertainty minimization）是不确定度抑制

---

与其他方法的对比结果

• 同样是10%的标签率，SL是监督学习
• 所有的半监督网络都以3D U-Net为backbone，URPC的表现是最好的

可视化结果

• 图a中，不确定的区域主要集中在分割目标的边界区域
• 图b中，随着标签率从10%提高到50%，URPC的dice指标一直是比DAN高的

我的实验

我在左心房数据集（LAHeart2018）上做的实验，一共154例数据，123例当做训练集，31例当做测试集。

Loss变化曲线

• 我这里的对比并不严谨，mean teacher网络里面的backbone是V-Net，URPC的backbone是U-Net
• 根据我自己做的实验，URPC效果在左心房核磁数据集上的表现，比MT没有多大提高

分割结果重建图：红色是金标签，蓝色是模型预测结果

• 相比只使用标注数据集的全监督方法，半监督方法不管是在评价指标或者可视化分割结果上，都是有显著提高的。

---

URPC的优点在于不修改网络结构，把U-Net网络中的多级特征利用起来，相互之间做一致性损失，并引入不确定度修正预测结果。

相比student-teacher网络，训练起来更加简单。

参考资料：
Luo X, Liao W, Chen J, et al. Efficient semi-supervised gross target volume of nasopharyngeal carcinoma segmentation via uncertainty rectified pyramid consistency[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2021: 318-329.

HiLab-git/SSL4MIS: Semi Supervised Learning for Medical Image Segmentation, a collection of literature reviews and code implementations.

项目地址：

LASeg: 2018 Left Atrium Segmentation (MRI)

---

如有问题，欢迎联系 ‘[email protected]’