深度学习——神经网络 Keras个人学习笔记
Keras:
技术文档 https://keras.io/api/
中文 https://keras-cn.readthedocs.io/en/latest/other/initializations/
Dense层
参数:
units:大于0的整数,代表该层的输出维度。
activation:激活函数,为预定义的激活函数名(参考激活函数),或逐元素(element-wise)的Theano函数。如果不指定该参数,将不会使用任何激活函数(即使用线性激活函数:a(x)=x)
use_bias: 布尔值,是否使用偏置项
kernel_initializer:权值初始化方法,为预定义初始化方法名的字符串,或用于初始化权重的初始化器。参考initializers
bias_initializer:偏置向量初始化方法,为预定义初始化方法名的字符串,或用于初始化偏置向量的初始化器。参考initializers
kernel_regularizer:施加在权重上的正则项,为Regularizer对象
bias_regularizer:施加在偏置向量上的正则项,为Regularizer对象
activity_regularizer:施加在输出上的正则项,为Regularizer对象
kernel_constraints:施加在权重上的约束项,为Constraints对象
bias_constraints:施加在偏置上的约束项,为Constraints对象
1.
keras.initializers.TruncatedNormal(mean=0.0, stddev=0.05, seed=None) #一般神经网络全连接层权重初始化为高斯分布
截尾高斯分布初始化,该初始化方法与RandomNormal类似,但位于均值两倍标准差以外的数据将会被丢弃并重新生成,形成截尾分布。该分布是神经网络权重和滤波器的推荐初始化方法。(类似于设置上下限)
mean:均值
stddev:标准差
seed:随机数种子
2.
kernel_regularizer=regularizers.l2(0.01)
#0.01 为惩罚力度,l2表示L2正则化(常用)
正则化
kernel是本层的权值矩阵
专业术语:
batch
深度学习的优化算法,说白了就是梯度下降。每次的参数更新有两种方式。
第一种,遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍,计算量开销大,计算速度慢,不支持在线学习,这称为Batch gradient descent,批梯度下降。
另一种,每看一个数据就算一下损失函数,然后求梯度更新参数,这个称为随机梯度下降,stochastic gradient descent。这个方法速度比较快,但是收敛性能不太好,可能在最优点附近晃来晃去,hit不到最优点。两次参数的更新也有可能互相抵消掉,造成目标函数震荡的比较剧烈。
为了克服两种方法的缺点,现在一般采用的是一种折中手段,mini-batch gradient decent,小批的梯度下降,这种方法把数据分为若干个批,按批来更新参数,这样,一个批中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性。另一方面因为批的样本数与整个数据集相比小了很多,计算量也不是很大。
基本上现在的梯度下降都是基于mini-batch的,所以深度学习框架的函数中经常会出现batch_size,就是指这个。
关于如何将训练样本转换从batch_size的格式可以参考训练样本的batch_size数据的准备。
iterations
iterations(迭代):每一次迭代都是一次权重更新,每一次权重更新需要batch_size个数据进行Forward运算得到损失函数,再BP算法更新参数。1个iteration等于使用batchsize个样本训练一次。
epochs
epochs被定义为向前和向后传播中所有批次的单次训练迭代。这意味着1个周期是整个输入数据的单次向前和向后传递。简单说,epochs指的就是训练过程中数据将被“轮”多少次,就这样。
举个例子
mnist 数据集有 60000 张图片作为训练数据,10000 张图片作为测试数据。假设现在选择 Batch Size = 100 对模型进行训练。迭代30000次。
- 每个 Epoch 要训练的图片数量:60000(训练集上的所有图像)
- 训练集具有的 Batch 个数: 60000/100=600
- 每个 Epoch 需要完成的 Batch 个数: 600
- 每个 Epoch 具有的 Iteration 个数: 600(完成一个Batch训练,相当于参数迭代一次)
- 每个 Epoch 中发生模型权重更新的次数:600
- 训练 10 个Epoch后,模型权重更新的次数: 600*10=6000
- 不同Epoch的训练,其实用的是同一个训练集的数据。第1个Epoch和第10个Epoch虽然用的都是训练集的60000图片,但是对模型的权重更新值却是完全不同的。因为不同Epoch的模型处于代价函数空间上的不同位置,模型的训练代越靠后,越接近谷底,其代价越小。
- 总共完成30000次迭代,相当于完成了 30000/600=50 个Epoch
损失函数(loss)
https://www.jianshu.com/p/ae3932eda8f2
定义:损失函数就一个具体的样本而言,模型预测的值与真实值之间的差距。
对于一个样本(xi,yi)其中yi为真实值,而f(xi)为我们的预测值。使用损失函数L(f(xi),yi)来表示真实值和预测值之间的差距。两者差距越小越好,最理想的情况是预测值刚好等于真实值。当真实输出a与期望输出y接近的时候,代价函数接近于0
1.均方差损失函数
简单来说,均方误差(MSE)的含义是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。
- 交叉熵categorical_crossentropy loss
是用来评估当前训练得到的概率分布与真实分布的差异情况。
它刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。
3.铰链损失函数Hinge loss
可用于“最大间隔(max-margin)”分类,其最著名的应用是作为SVM的损失函数。
4.keras的损失函数计算集合
Dropout
防止数据过拟合,随机暂时“放弃”一些神经元
ropout 是一种计算方便但功能强大的正则化方法,适用于最近很火的神经网络。他的基本步骤是在每一次的迭代中,随机删除一部分节点,只训练剩下的节点。每次迭代都会随机删除,每次迭代删除的节点也都不一样,相当于每次迭代训练的都是不一样的网络,通过这样的方式降低节点之间的关联性以及模型的复杂度,从而达到正则化的效果。这点上有点类似 bagging,但是远比 bagging 来的简单。

说dropout简单是因为你只需要设置一个超参数 keep_prob,这个参数的意义是每层节点随机保留的比例,比如将 keep_prob 设置为 0.7,那么就会随机30%的节点消失,消失这个动作其实很简单,只是将这一层的参数矩阵与根据 keep_prob 生成的 {0, 1} 矩阵做 逐点乘积,当然前向传播与反向传播都需要做以上的操作。
dropout的缺点在于,需要将训练集分为不同子集输入每一次的迭代,这就需要较大的训练集,所以在训练集较小的情况下,dropout的效果可能并不好。我们上面也说过,增大数据集是最好的正则化方式,所以在增大数据集的情况下,使用 dropout 需要使用的计算代价可能会比他带来正则化效果更高,这需要我们在实际使用场景中做取舍。一般由于全连接层而非卷积层
one-hot向量
one-hot向量将类别变量转换为机器学习算法易于利用的一种形式的过程,这个向量的表示为一项属性的特征向量,也就是同一时间只有一个激活点(不为0),这个向量只有一个特征是不为0的,其他都是0,特别稀疏。
举个例子:一个特征“性别”,性别有“男性”、“女性”,这个特征有两个特征值,也只有两个特征值,如果这个特征进行one-hot编码,则特征值为“男性”的编码为“10”,“女性”的编码为“01”,如果特征值有m个离散特征值,则one-hot后特征值的表示是一个m维的向量,每个样本的特征只能有一个值,这个值的向量坐标上就是1,其他都是0,如果有多个特征,“性别”有两个特征,“尺码”:M、L、XL三个值,我们用“01”表示男性,M为“100”,L为“010”,XL为“001”,所以一个样本,【“男性”、“L”】 one-hot编码为[10 010],一个样本也就是5维的向量,这就是one-hot形式。
Batch_normalization
BN来源:
BN原因:
随着网络的深度增加,每层特征值分布会逐渐的向激活函数的输出区间的上下两端(激活函数饱和区间)靠近,这样继续下去就会导致梯度消失。BN就是通过方法将该层特征值分布重新拉回标准正态分布,特征值将落在激活函数对于输入较为敏感的区间,输入的小变化可导致损失函数较大的变化,使得梯度变大,避免梯度消失,同时也可加快收敛。
过程:input={x1,x2,x3…xn}
1 计算 x1-xn的均值u
2 计算x1-xn的方差v
3 每个x_i = (x_i – u) / (sqrt(v^2)+ e) e是一个小小偏置,防止分母趋向于0.
4 在对结果进行scale于shift操作 x_i = scale*x_i + shift
第四步存在的原因是batch_normal后,数据趋向标准正态,会导致网络表达能力变差,这里加入后标准正态分布有些偏移,变得不那么标准了。这两个参数时学习而来
Regularization 正则化
https://www.jianshu.com/p/569efedf6985
正则化的概念及原因
简单来说,正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。我们在构造机器学习模型时,最终目的是让模型在面对新数据的时候,可以有很好的表现。当你用比较复杂的模型比如神经网络,去拟合数据时,很容易出现过拟合现象(训练集表现很好,测试集表现较差),这会导致模型的泛化能力下降,这时候,我们就需要使用正则化,降低模型的复杂度。
正则化就是对最小化经验误差函数上加约束,这样的约束可以解释为先验知识(正则化参数等价于对参数引入先验分布)。约束有引导作用,在优化误差函数的时候倾向于选择满足约束的梯度减少的方向,使最终的解倾向于符合先验知识(如一般的l-norm先验,表示原问题更可能是比较简单的,这样的优化倾向于产生参数值量级小的解,一般对应于稀疏参数的平滑解)。同时,正则化解决了逆问题的不适定性,产生的解是存在,唯一同时也依赖于数据的,噪声对不适定的影响就弱,解就不会过拟合,而且如果先验(正则化)合适,则解就倾向于是符合真解(更不会过拟合了),即使训练集中彼此间不相关的样本数很少。两者都是通过加上一个和项来限制参数大小,却有不同的效果: 正则化
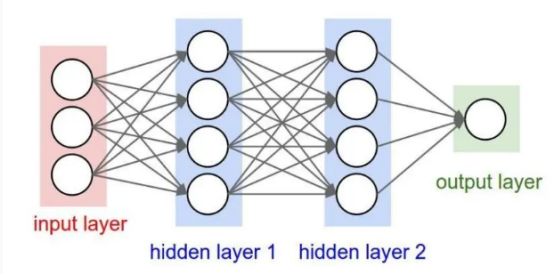
- 层级结构:
数据输入层/ Input layer
卷积计算层/ CONV layer
ReLU激励层 / ReLU layer
池化层 / Pooling layer
全连接层 / FC layer
1)数据输入层
该层要做的处理主要是对原始图像数据进行预处理,其中包括:
- 去均值:把输入数据各个维度都中心化为0,如下图所示,其目的就是把样本的中心拉回到坐标系原点上。
- 归一化:幅度归一化到同样的范围,如下所示,即减少各维度数据取值范围的差异而带来的干扰,比如,我们有两个维度的特征A和B,A范围是0到10,而B范围是0到10000,如果直接使用这两个特征是有问题的,好的做法就是归一化,即A和B的数据都变为0到1的范围。
- PCA/白化:用PCA降维;白化是对数据各个特征轴上的幅度归一化


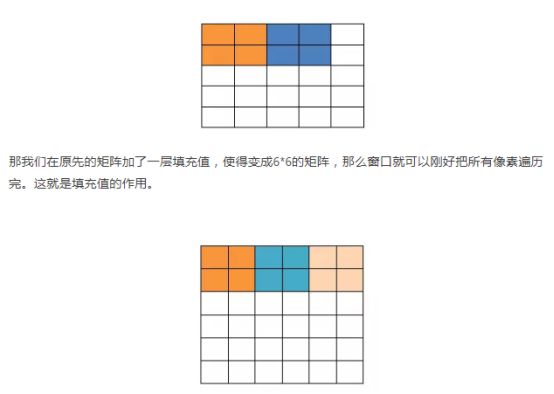
填充值是什么呢?以下图为例子,比如有这么一个5 * 5的图片(一个格子一个像素),我们滑动窗口取2*2,步长取2,那么我们发现还剩下1个像素没法滑完,那怎么办呢?
卷积计算:
这里的蓝色矩阵就是输入的图像,粉色矩阵就是卷积层的神经元,这里表示了有两个神经元(w0,w1)。绿色矩阵就是经过卷积运算后的输出矩阵,这里的步长设置为2。
蓝色的矩阵(输入图像)对粉色的矩阵(filter)进行矩阵内积计算并将三个内积运算的结果与偏置值b相加(比如上面图的计算:2+(-2+1-2)+(1-2-2) + 1= 2 - 3 - 3 + 1 = -3),计算后的值就是绿框矩阵的一个元素。
参数共享机制
- 在卷积层中每个神经元连接数据窗的权重是固定的,每个神经元只关注一个特性。神经元就是图像处理中的滤波器,比如边缘检测专用的Sobel滤波器,即卷积层的每个滤波器都会有自己所关注一个图像特征,比如垂直边缘,水平边缘,颜色,纹理等等,这些所有神经元加起来就好比就是整张图像的特征提取器集合。
- 需要估算的权重个数减少: AlexNet 1亿 => 3.5w
- 一组固定的权重和不同窗口内数据做内积: 卷积

3)激励层
把卷积层输出结果做非线性映射。
axon 轴突 synapse突触 activation funcion 激励函数
CNN采用的激励函数一般为ReLU(The Rectified Linear Unit/修正线性单元),它的特点是收敛快,求梯度简单,但较脆弱,图像如下。
Sigmoid:S型生长曲线
4)池化层
池化层夹在连续的卷积层中间, 用于压缩数据和参数的量,减小过拟合。
简而言之,如果输入是图像的话,那么池化层的最主要作用就是压缩图像。
这里再展开叙述池化层的具体作用。
- 特征不变性,也就是我们在图像处理中经常提到的特征的尺度不变性,池化操作就是图像的resize,平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片,这说明这张图像中仍保留着狗最重要的特征,我们一看就能判断图像中画的是一只狗,图像压缩时去掉的信息只是一些无关紧要的信息,而留下的信息则是具有尺度不变性的特征,是最能表达图像的特征。
- 特征降维,我们知道一幅图像含有的信息是很大的,特征也很多,但是有些信息对于我们做图像任务时没有太多用途或者有重复,我们可以把这类冗余信息去除,把最重要的特征抽取出来,这也是池化操作的一大作用。
- 在一定程度上防止过拟合,更方便优化。
池化层用的方法有Max pooling 和 average pooling,而实际用的较多的是Max pooling。这里就说一下Max pooling,其实思想非常简单。
5)全连接层 dense
两层之间所有神经元都有权重连接,通常全连接层在卷积神经网络尾部。也就是跟传统的神经网络神经元的连接方式是一样的:
优缺点
优点
•共享卷积核,对高维数据处理无压力
•无需手动选取特征,训练好权重,即得特征分类效果好
缺点
•需要调参,需要大样本量,训练最好要GPU
•物理含义不明确(也就说,我们并不知道每个卷积层到底提取到的是什么特征,而且神经网络本身就是一种难以解释的“黑箱模型”)
常用框架
Caffe
•源于Berkeley的主流CV工具包,支持C++,python,matlab
•Model Zoo中有大量预训练好的模型供使用
Torch
•Facebook用的卷积神经网络工具包
•通过时域卷积的本地接口,使用非常直观
•定义新网络层简单
TensorFlow
•Google的深度学习框架
•TensorBoard可视化很方便
•数据和模型并行化好,速度快
总结
卷积网络在本质上是一种输入到输出的映射,它能够学习大量的输入与输出之间的映射关系,而不需要任何输入和输出之间的精确的数学表达式,只要用已知的模式对卷积网络加以训练,网络就具有输入输出对之间的映射能力。
CNN一个非常重要的特点就是头重脚轻(越往输入权值越小,越往输出权值越多),呈现出一个倒三角的形态,这就很好地避免了BP神经网络中反向传播的时候梯度损失得太快。
卷积神经网络CNN主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。由于CNN的特征检测层通过训练数据进行学习,所以在使用CNN时,避免了显式的特征抽取,而隐式地从训练数据中进行学习;再者由于同一特征映射面上的神经元权值相同,所以网络可以并行学习,这也是卷积网络相对于神经元彼此相连网络的一大优势。卷积神经网络以其局部权值共享的特殊结构在语音识别和图像处理方面有着独特的优越性,其布局更接近于实际的生物神经网络,权值共享降低了网络的复杂性,特别是多维输入向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。
两大特点:
1)局部感知
因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。网络部分连通的思想,也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的(即这些神经元只响应某些特定区域的刺激)。
- 参数共享
当从一个大尺寸图像中随机选取一小块,比如说 8x8 作为样本,并且从这个小块样本中学习到了一些特征,这时我们可以把从这个 8x8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,我们可以用从 8x8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
一维离散卷积运算:
- 一维卷积神经网络处理时间序列数据
https://juejin.im/post/5beb7432f265da61524cf27c
https://keras.io/guides/sequential_model/
1.何时应用
1D CNN 可以很好地应用于传感器数据的时间序列分析(比如陀螺仪或加速度计数据);同样也可以很好地用于分析具有固定长度周期的信号数据(比如音频信号)。此外,它还能应用于自然语言处理的任务(由于单词的接近性可能并不总是一个可训练模式的好指标,因此 LSTM 网络在 NLP 中的应用更有前途)。