PCA方法的分解过程_协方差矩阵+特征值分解+降维投影

问题引入

调用sklearn库时，使用decomposition.PCA(n_components=2)就可以把多维的数据降至两维，里面的过程一概不知，看起来像个黑盒，心里面很没有底。今天小王同学就来尝试解答以下问题
1）主成分分析法PCA里的分解过程是什么样的？基于什么原理
2）相对原数据，它保留了哪些信息，又损失了什么？怎么科学选择成分的数量？

代码部分参考自Sebastian Raschka的博客pca_in_3_steps，感谢原作大神

PCA的实现

1. 数据集加载

作为其他学习资料的一个补充，概念部分不多赘述。概括来说，我们对一个D维的数据集运用PCA，希望最大化M维子空间的保留信息，同时最小化（D-M）维空间上的损失信息。今天以代码层层递进的形式，结合图像对分解过程和主成分选取进行说明。

首先，我们准备经典数据集iris，在sklearn数据库中即可加载

from sklearn import datasets

# 加载数据
iris = datasets.load_iris()
# help(datasets.load_iris)  # Check the data struture

X = iris.data # Each row is an observation, each col is a variable
y = iris.target
print(" The shape of X and y ", X.shape, y.shape,"\n", 
    "Features are ", iris.feature_names, "\n", "Classes are ", iris. target_names)

The shape of X and y  (150, 4) (150,) 
 Features are  ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] 
 Classes are  ['setosa' 'versicolor' 'virginica']

2. 数据预处理

这一步，自己尝试了MinMax scaling，由于petal length特征的值域过大，最大最小化缩放后，特征三和其余四个特征不在一个数量级。考虑到数量级的差异对PCA这种距离敏感型算法，容易造成影响。故采用了原作者的Z-score归一化方法，其他方法笔者未试验效果。

from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)

对于调库的细节，特别补充说明下，查阅资料时发现一些数据大神们会强调不同归一化方法之间的区别。比如最容易和StandardScaler方法混淆的Normalizer，这里整理如下（描述引用自sklearn官方文档）

• StandardScaler - Standardize features by removing the mean and scaling to unit variance.
  重点，按每列（不同的特征）进行操作，与样本均值的相对差值 / 样本方差
• Normalizer - Each sample (i.e. each row of the data matrix) with at least one non zero component is rescaled independently of other samples so that its norm (l1, l2 or inf) equals one.
  重点，按每一行（不同的样本点）进行操作，把整行做单位距离归一化

3. 主成分分解

3.1 协方差矩阵构造

这里，样本协方差矩阵（Sample covariance matrix）采用其原始定义进行求解。它的第i行第j列的单个元素可表示为Cov(X_i，X_j)，其中X_i，X_j分别对应着样本集的第i列和第j列特征数据，k代表观察值序号（k=1,2,…,n），则有矩阵元素：
$$Cov(X_i,X_j)=\frac{1}{n}\sum _{k=1}^n(x_{i,k}-E(X_i))(x_{j,k}-E(X_j))$$

import numpy as np
X_train = X_std # Create a reference to the origin
X_mean = np.mean(X_train, axis=0)   # A vector with size (4,)
n = X_train.shape[0]
X_cov = (X_train - X_mean).T @ (X_train - X_mean) / n
X_cov   # A symmetric matrix with size (4,4)

可以通过np.cov(X_train.T, bias=True)实现同样的结果，但要注意输入样本矩阵的形状。同时，更直观的，我们把协方差矩阵可视化：

图1）鸢尾花数据集的样本协方差矩阵，绘制代码可参考附录资料2

3.2 特征值分解

对于一个对称矩阵来说，对应于不同特征值的特征向量，必定彼此具有正交性。如果再将这一组特征向量分别做归一化（normalization）处理，就能得到一组单位正交向量，进而组成正交矩阵（orthogonal matrix）。

# 计算协方差矩阵的特征值、特征向量
import numpy as np
eig_val, eig_vec = np.linalg.eig(X_cov)

# 检验得到的是否为单位正交矩阵，即每一列的norm和为1
for ev in eig_vec.T:
    np.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev))
    
# 这里直接用assert，标准过高，浮点误差会报错
# numpy自带的assert almost，默认精度为六位，可设置参数decimal修改
# 方法二，也可使用u,s,v = np.linalg.svd(X_std.T)，eig_vec = u
print("Eigen values\n", eig_val, "\nEigen vectors\n", eig_vec)

Eigen values
 [2.93808505 0.9201649  0.14774182 0.02085386] 
Eigen vectors
 [[ 0.52106591 -0.37741762 -0.71956635  0.26128628]
 [-0.26934744 -0.92329566  0.24438178 -0.12350962]
 [ 0.5804131  -0.02449161  0.14212637 -0.80144925]
 [ 0.56485654 -0.06694199  0.63427274  0.52359713]]

3.3 方差解释

回到我们开头提出的问题，已经得到了特征值和特征向量，但到底选用多少维度合适，是我们这次希望了解的。
对于鸢尾花数据集来说，维度小还能直观看出，但面对以后的研究和工作，我们需要掌握一定的分析方法。下面介绍其中一种——利用降序排列的特征值累计求和（Cumulative sum）的方法：

tot = sum(eig_val)
var_exp = [(i / tot)*100 for i in sorted(eig_val, reverse=True)]
cum_var_exp = np.cumsum(var_exp) # Return a cumulative sum
print("Cumulative sum \n", cum_var_exp)

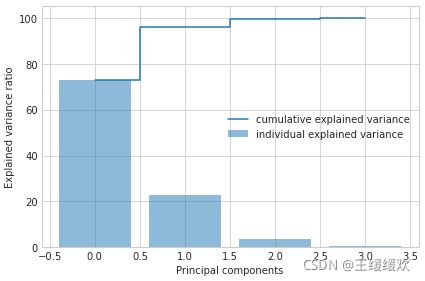
图2）鸢尾花数据集的特征值累计求和，绘制代码可参考附录资料1

从图像中可以看到绝大多数方差（72.96%）能被第一个主成分解释，再加上第二个主成分，两者共能解释95%以上的方差。

3.4 降维投影

我们知道降维方法在追求简化的过程中，希望尽可能大的保留所需的原始信息。前两项主成分已经能解释绝大多数的数据变化（通常需要在80%以上），这时其余主成分被舍弃，就不至于损失太多信息。因此，在该案例下，选择降维至二维子空间是一个合理的决定。

# 根据上述的分析，选用前两个主成分进行降维

proj_mat = np.hstack((eig_vec[:, 0].reshape(-1,1), 
                      eig_vec[:, 1].reshape(-1,1)))
print('Projection matrix\n', proj_mat)
Y = X_std @ proj_mat # Y即是我们最终需要的降维结果

Projection matrix
 [[ 0.52106591 -0.37741762]
 [-0.26934744 -0.92329566]
 [ 0.5804131  -0.02449161]
 [ 0.56485654 -0.06694199]]

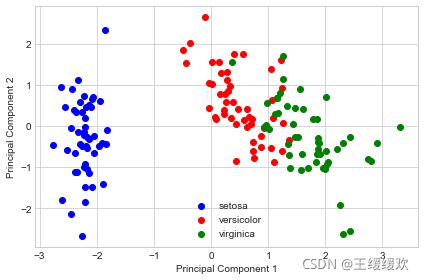
3.5 降维结果

target_names = ['setosa','versicolor','virginica']

with plt.style.context('seaborn-whitegrid'):
    plt.figure(figsize=(6, 4))
    for lab, col in zip((0, 1, 2),
                        ('blue', 'red', 'green')):
        plt.scatter(Y[y==lab, 0],
                    Y[y==lab, 1],
                    label=target_names[lab],
                    c=col)
    plt.xlabel('Principal Component 1')
    plt.ylabel('Principal Component 2')
    plt.legend(loc='lower center')
    plt.tight_layout()
    plt.show()

问题总结

本次，我们尝试拆解了PCA的实现过程，并知道如何合理筛选维度数。但依旧有一些未尽的工作。包括以下部分：

1. 对于异常值的识别没有做。由于PCA方法中，涉及计算样本均值和方差，而这些统计值对异常值（outliers）的干扰非常敏感，需要留心。
2. 未讨论更多的成分选取方法。是否选择80%以上解释程度的成分就是最佳选择，还有没有其他合理的选择方法，本次并未深究。
3. 未与LDA、ICA等其他降维方法做对比。PCA的时间复杂度和作为线性变换的局限并没有进一步讨论。

附录

参考资料：

1. https://sebastianraschka.com/Articles/2015_pca_in_3_steps.html （代码部分均参考此文档，感谢原作，非常详尽）
2. https://www.statology.org/covariance-matrix-python/#:~:text=A covariance matrix is a square matrix that,steps to create a covariance matrix in Python.
3. https://stackoverflow.com/questions/39120942/difference-between-standardscaler-and-normalizer-in-sklearn-preprocessing

---

经验有限，如有错误，欢迎指正