线性回归
引子
这一期我们讨论机器学习中的回归问题。
认真看过上一期的同学应该记得,回归属于监督学习中的一类方法。简单来讲,回归就是通过数据学习数量关系,然后利用这个数量关系去做预测。
作为人类,我们能轻而易举地学习并理解现实中的简单数量关系。隔壁老王的SUV每100公里耗油10升,出门往返200公里,老王就知道该给车加至少20升油。why?因为连他8岁的儿子都知道这就是个简单的正比例关系。
然而数量关系并不都是那么简单。老王昨天一人食点了个9寸海鲜披萨,刚刚饱。这次他心血来潮带老婆一块去吃,掐指一算点了个18寸的。最后的结局当然是撑得生无可恋,双双扶墙回家。
看,通过逻辑思考总结数量关系,在不同情境下我们需要调用不同的思考逻辑,因而容易出错。为此,我们很难给计算机讲道理,告诉它为什么SUV的耗油量和里程数之间是正比关系,披萨的尺寸和食用人数之间却又不是了。更何况还有像“南半球的一只蝴蝶扇了扇翅膀,北半球的纳斯达克就崩盘”这种超出人类逻辑理解范围的复杂关系。靠人类总结规律再教给计算机,就更不可能了。
所以,回归的策略是跳过逻辑分析,让计算机直接从数据中学习数量关系。这正是机器学习(统计学习)的核心思想。因此回归除了作为一种机器学习算法,也是一个超出描述层面统计分析,关注现象解释和预测的统计模型。
回归这个名词看上去颇为不接地气。其实说来有趣,追根溯源,回归(Regression)这一概念最早是由英国生物统计学家高尔顿和他的学生皮尔逊在研究父母亲和子女的身高遗传特性时提出的。他们的研究揭示了关于身高的一个有趣的遗传特性:若父母个子高,其子代身高高于平均值的概率很大,但一般不会比父母更高。即身高到一定程度后会往平均身高方向发生“回归”。这种效应被称为“趋中回归(Regression Toward the Mean)”。如今,所讨论的“回归”和这种趋中效应已经没有任何瓜葛了,它只是指源于高尔顿工作的那样一整套建立变量间数量关系模型的方法和程序。然而回归这个朗朗上口的名字却歪打正着一直流传至今。
在一个回归模型中,我们需要关注或预测的变量叫做因变量(响应变量或结果变量),我们选取的用来解释因变量变化的变量叫做自变量(解释变量或预测变量)。做回归分析,确定变量后我们还需要根据具体问题选择一个合适的回归模型,通俗地说就是把自变量映到因变量的函数的大体样子。常用的回归模型有线性回归,多项式回归,逻辑回归等等。考虑到线性关系是自然界最普遍,最本质的数量关系,所以毋庸置疑线性回归是最简单实用的一类回归模型,也是其他回归模型研究的基础。下面我们讨论线性回归(前方干货,高能预警)。
线性回归的数学基础
从最简单的一元线性回归说起。现有自变量 X ,因变量Y,对具体问题,我们拿到的观测值是 (x1,y1),...,(xn,yn) .回归方程为
其中 k,b 是待学习的参数, ε 为残差。我们的目标是找到一条直线 y=kx+b 使得所有样本点尽可能落在它的附近。之所以这样做,是因为我们相信 X 和Y 之间就应该差不多满足这个简单的关系。
若确实有这么个一次函数让所有数据都满足条件,那这就成了SUV耗油问题,隔壁老王的儿子也能一眼看出来。我们面临的真正挑战在于,来自现实的数据是有误差的,一般来说无法保证所有的样本点都精确满足回归方程。所以我们只能退而求其次,给计算机安排的学习策略就是在某种意义上让误差 ε 取到极小,以期望得到最可能接近真实规律的模型。在高中我们就熟知这个问题的解法——求解使得 εi(i=1,2,…,n) 的平方和极小化的 k,b :
以上关于 (k,b) 的无约束二次优化问题,其解析解是容易得到的。这就是大名鼎鼎的最小二乘法(Ordinary Least Square, OLS)。直观上,这个算法给出了描述 X,Y 两个变量线性关系的最优近似。
多元线性回归本质也是一样,只是自变量和参数的个数变为多个。我们的目标仍是在最小二乘的意义下找到让残差平方和取极小的参数。模型为
其中 Y=(y1,...,yn)T 为因变量,有 n 个观测值;X=(xij)n×k 为 n×k 矩阵,其 k 个列分别表示k 个自变量的 k×n 个观测值; β=(β1,...,βk) 为自变量的回归系数, ε 为残差。若考虑截距项,可在 X 中加入一列常数,出于简单起见暂不考虑。
这个问题在OLS意义下的解为
上式称作法方程(Normal Equation)。
不难看出,回归模型训练的关键在于确定一个残差极小化准则,数学上讲,就是指定一个损失函数(Loss Function)。一般来讲我们所说的线性回归都是在最小二乘(OLS)准则下得到的模型。其他的选择也是有的,如最小一乘模型(残差绝对值之和极小),以及在损失函数中加入对模型复杂度的惩罚项后得到的各种带正则化的回归模型(岭回归,LASSO等)。这些高端方法有兴趣的读者可以自行了解。
线性回归的数学本质
深入理解线性回归的钥匙在于最小二乘条件。1829年高斯提出最小二乘法,但早在1760年波斯科维奇就提出了最小一乘法。最小一乘在数学上更简单也更符合人们的直觉,但为什么人们却对最小二乘法如此青睐呢?我看来有以下两个原因:
从线性代数的角度来看,多元回归是一个典型的最佳逼近问题。即在 X 的列向量所张成的k维线性空间 Vk 中找一个元素 Yk=Xβ ,使得 Yk∈Vk 与 Y∈Vn 在某种度量的意义下距离最短。于是自然地,我们选取欧氏距离作为度量,这就是OLS中残差平方和的由来。
具体来讲,选取欧氏距离的好处在于使得线性空间 Vn 及其子空间 Vk 成为内积空间,从而具备了良好的几何性质。在欧氏度量的意义下, Y 在Vk中的最佳逼近元 Yk 正是 Y 在Vk上的正交投影,于是我们有
ε=(Y−Yk)⊥Vk
即 ε⊥X,XTε=0 .这样一来,在回归方程的两边同时左乘 (XTX)−1XT 立刻解得 β∗=(XTX)−1XTY .这就是法方程的由来。从数理统计的角度来看,多元回归是一个典型的参数估计问题。OLS的好处在于,在一定条件条件下由它得到的估计量拥有诸多统计学上的优良性质。严格来说,需对模型提以下条件:
1、误差 ε 是一个期望0的随机向量;
2、对于解释变量的所有观测值, ε 的各个分量有相同的方差,且彼此不相关;
3、解释变量与随机误差项彼此相互独立;
4、解释变量之间不存在精确的线性关系;
5、随机误差项服从正态分布。
在条件1,2,3,4成立的前提下,我们有著名的高斯-马尔科夫定理:最小二乘估计是最小方差线性无偏估计。在5个条件全部成立的前提下,还不难证明最小二乘估计是极大似然估计。
理论上第5个条件并不是硬性的,但实际问题中我们一般希望它能够满足。毕竟,若只要模型足够好以至于选取的自变量确实与因变量线性相关,那么残差与预测值就应该没有任何系统关联,于是当数据量足够大时它理应服从正态分布。此外,残差满足正态分布的假设还有助于我们在做回归结果诊断时对模型参数进行显著性检验。
回归模型的有效性
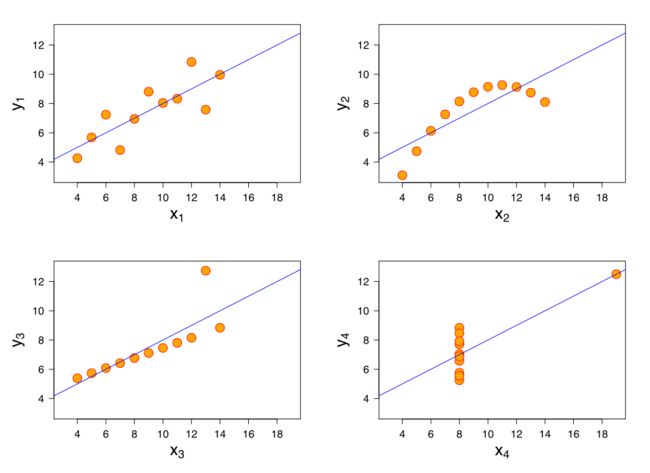
事实上,无论数据是否满足模型基本假设,理论上都是可以通过最小二乘法得到模型参数的。只不过此时模型的有效性就要打问号了(最小二乘君:怪我咯)。为此我们来看一个著名例子(Anscombe’s quartet,图片来自维基百科):
对这四组观测数据,我们用线性回归将得到完全相同的模型,但它们的解释力显然大相径庭。最小二乘君是冤枉的,问题出在数据上!上一期我们提到过,模型是火箭,数据是燃料。燃料兑了水火箭还能升空,最小二乘君已经尽力了有木有。对燃料进行提纯,浓缩,也就是数据预处理的工作,应当落在数据科学家的头上。具体来讲,在接受一个回归模型之前需要对数据进行的检验包括但不仅限于下面几条:
1. 残差是否近似满足均值为0的正态分布;
2. 因变量值是否独立;
3. 是否存在离群点,高杠杆值点或强影响点。
当预处理后的数据基本满足模型假设,我们可以接受回归模型的结果之后,还需要设计一些指标去衡量它的效果。常见的如衡量模型拟合优度的 R2 值,衡量拟合方程的显著性的F值以及衡量各个变量拟合系数的显著性的t值等。这些也都是数据科学家要做的具体工作,细节就不赘述了。
所有检验通过之后,我们总算得到了一个看上去靠谱的回归模型。但还不够!计算机只是客观告诉我们一堆数据中极有可能隐藏着某个数量关系;而回答为什么有这种关系,并不是它的长项。所以,解释模型的艰巨任务自然也落到了数据科学家头上。数据科学家需要结合业务实际和常识,告诉人们为什么这些回归系数理应是模型推算出来的那个样子。可不要小看模型解释哦,很多时候一个模型是否能在实际中发挥作用,很大程度上在于能不能赋予它一个合乎逻辑的解释。想想转基因食品吧,所有的数据都一边倒地证明转基因无害没有任何卵用,只要一天科学家给不出铁板钉钉的理论支持,就总有人视其为洪水猛兽,唯恐避之不及。这也无可厚非,毕竟生命不比程序,可以随时推倒重来。
统计学大牛George Box曾经曰过:All models are wrong, but some are useful.最后用这句话来总结线性回归再恰当不过。自然界错综复杂,但大部分现象都能用最最简洁优美的线性关系来描述。线性回归作为一个粗糙暴力的模型,误差在所难免,但对我们理解这个世界已然实现了从0到1的跨越。这一期的科普就到这里。下一期我们讲逻辑回归。