机器学习:Universal Stagewise Learning for Non-Convex Problems with Convergence on Averaged Solutions

Abstract

• Although stochastic gradient descent (SGD) method and its variants (e.g., stochastic momentum methods, ADAGRAD) are the choice of algorithms for solving non-convex problems (especially deep learning), there still remain big gaps between the theory and the practice with many questions unresolved. For example, there is still a lack of theories of convergence for SGD and its variants that use stagewise step size and return an averaged solution in practice. In addition, theoretical insights of why adaptive step size of ADAGRAD could improve non-adaptive step size of SGD is still missing for non-convex optimization. This paper aims to address these questions and fill the gap between theory and practice. We propose a universal stagewise optimization framework for a broad family of non-smooth non-convex (namely weakly convex) problems with the following key features:(i) at each stage any suitable stochastic convex optimization algorithms (e.g., SGD or ADAGRAD) that return an averaged solution can be employed for minimizing a regularized convex problem; (ii) the step size is decreased in a stagewise manner;(iii) an averaged solution is returned as the final solution that is selected from all stagewise averaged solutions with sampling probabilities increasing as the stage number. Our theoretical results of stagewise ADAGRAD exhibit its adaptive convergence, therefore shed insights on its faster convergence for problems with sparse stochastic gradients than stagewise SGD. To the best of our knowledge, these new results are the first of their kind for addressing the unresolved issues of existing theories mentioned earlier. Besides theoretical contributions, our empirical studies show that our stagewise SGD and ADAGRAD improve the generalization performance of existing variants/implementations of SGD and ADAGRAD.
• 虽然随机梯度下降(SGD)方法及其变体(如随机动量法、ADAGRAD)是求解非凸问题(尤其是深度学习)的算法选择，但理论与实践之间仍存在较大差距，许多问题尚未解决。例如，对于SGD及其变体，仍然缺乏使用阶段级步长并在实践中返回平均解的收敛理论。此外，对于ADAGRAD的自适应步长为何能够改善SGD的非自适应步长，对于非凸优化仍然缺乏理论见解。本文旨在解决这些问题，填补理论与实践之间的空白。针对一类广义非光滑非凸(即弱凸)问题，我们提出了一种通用的阶段优化框架，其主要特征如下:(i)在每一阶段，任何合适的随机凸优化算法(如SGD或ADAGRAD)都可以用平均解最小化正则凸问题;(ii)按阶段减小步长;(iii)从所有阶段平均解中选择一个平均解作为最终解返回，采样概率随着阶段数的增加而增加。我们的分段ADAGRAD理论结果显示了它的自适应收敛性，因此对于稀疏随机梯度问题，它比分段SGD具有更快的收敛速度。据我们所知，这些新结果是第一次解决了先前提到的现有理论中尚未解决的问题。除了理论贡献，我们的实证研究表明，我们的阶段性SGD和ADAGRAD改进了现有SGD和ADAGRAD的变种/实现的泛化性能。

1. Introduction

目前背景：

• First, a heuristic for setting the step size in training deep neural networks is to change it in a stagewise manner from a large value to a small value (i.e., a constant step size is used in a stage for a number of iterations and is decreased for the next stage) [25], which lacks theoretical analysis to date. In existing literature [14, 7], SGD with an iteratively decreasing step size or a small constant step size has been well analyzed for non-convex optimization problems with guaranteed convergence to a stationary point. For example, the existing theory usually suggests an iteratively decreasing step
  size proportional to 1/√t .

• 首先，在训练深度神经网络时，设置步长的启发式方法是将其从一个大的值逐步变为一个小的值。，某阶段迭代次数为常数步长，下一阶段减小)[25]，目前缺乏理论分析。已有文献[14,7]对保证收敛到平稳点的非凸优化问题，很好地分析了步长迭代递减或步长较小的SGD。例如,现有的理论通常表明一个迭代步长减少比例为1 /√t

  https://blog.csdn.net/weixin_43414866/article/details/99228292
  

• Second, the averaging heuristic is usually used in practice, i.e., an averaged solution is returned for prediction [3], which could yield improved stability and generalization.

• 其次，在实际应用中，通常采用平均启发式方法，返回预测的平均解，从而提高了预测的稳定性和泛化能力。然而，这两个选项在实践中很少使用.

• A third common heuristic in practice is to use adaptive coordinate-wise step size of ADAGRAD [9]. Although adaptive step size has been well analyzed for convex problems (i.e., when it can yield faster convergence than SGD) [12, 5], it still remains an mystery for non-convex optimization with missing insights from theory. Several recent studies have attempted to analyze ADAGRAD for non-convex problems [37, 27, 4, 45]. Nonetheless, none of them are able to exhibit the adaptive convergence of ADAGRAD to data as in the convex case and its advantage over SGD for non-convex problems.

• 第三种常见的启发式方法是使用ADAGRAD的自适应协调步长。虽然自适应步长已经很好地分析了凸问题,但是非凸优化仍然是一个谜，缺乏理论的支持。

To overcome the shortcomings of existing theories for stochastic non-convex optimization, this paper analyzes new algorithms that employ some or all of these commonly used heuristics in a systematic framework.

为了克服现有随机非凸优化理论的不足，本文分析了在系统框架中采用部分或全部这些常用启发式算法的新算法.

2. Preliminaries
预选策略

The problem of interest in this paper is:

min x∈Ω φ(x) = E_ξ [φ(x; ξ)]

where Ω is a closed convex set, ξ ∈ U is a random variable, φ(x) and φ(x; ξ) are non-convex functions, with the basic assumptions on the problem given in Assumption 1.
Ω是一个封闭的凸集,ξ∈U是一个随机变量,φ(x)和φ(x;ξ)非凸函数,基本假设的问题给出了假设1.[Assumption 1]

To state the convergence property of an algorithm for solving the above problem. We need to intro-
duce some definitions. These definitions can be also found in related literature, e.g., [8, 7]. In the
sequel, we let || · || denote an Euclidean norm, [S] = {1, . . . , S} denote a set, and δΩ(·) denote the
indicator function of the set Ω.

说明求解上述问题的算法的收敛性。我们需要介绍,一些定义。这些定义也可以在相关文献中找到.例如,我们让 || · ||表示欧几里得范数,[S] = {1,…，S}表示一集合,δΩ(·)表示的指标函数设置Ω。

Definition 1. (Fr´echet subgradient) For a non-smooth and non-convex function f(·),

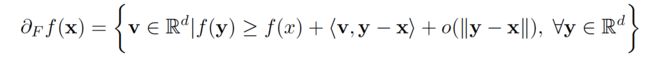
denotes the Fr´echet subgradient of f.

对于非光滑非凸函数f(·), 上述表达式表示f(·)Fr’ echet 次梯度.

Definition 2. (First-order stationarity) For problem (1), a point x ∈ Ω is a first-order stationary point if
where δΩ denotes the indicator function of Ω. Moreover, a point x is said to be ǫ-stationary if
where dist denotes the Euclidean distance from a point to a set.

Definition 3. (Moreau Envelope and Proximal Mapping) For any function f and λ > 0, the follow-ing function is called a Moreau envelope of f
(莫罗包络线与邻近映射)
对于任何函数f和λ> 0,下面的函数称为f的莫罗包络线

Further, the optimal solution to the above problem denoted by
进一步，上述问题的最优解为：

is called a proximal mapping of f.
称作f的邻近映射

Definition 4. (Weakly convex) A function f is ρ-weakly convex, if f(x) + ρ2 || x || ² is convex.
It is known that if f(x) is ρ-weakly convex and λ < ρ−1, then its Moreau envelope fλ(x) is C1-smooth with the gradient given by (see e.g. [7])
函数f是一个 ρ-weakly凸函数，如果f(x) + ρ2 || x || ^2也是凸函数，众所周知,如果f (x) =ρ-weakly是凸凸函数并且λ<ρ−1,那么它的莫罗包络线f_λ(x)梯度为:

A small norm of ∇f_λ(x) has an interpretation that x is close to a point that is nearly stationary. In particular for any x ∈ R , let x^ = prox_λf (x), then we have
一小规范∇f_λ(xd)有一个解x接近这一点几乎是稳定的。特别是对于任何x∈R,让 x^ = prox_λf (x),然后我们有

This means that a point x satisfying ||∇fλ(x)|| ≤ ǫ is close to a point in distance of O(ǫ) that is ǫ-stationary.
这意味着x满足 ||∇fλ(x)||≤ǫ 即x-x^接近于O(ǫ), 那么称之为 ǫ-stationary.