机器学习入门八

聚类算法

定义

无监督算法

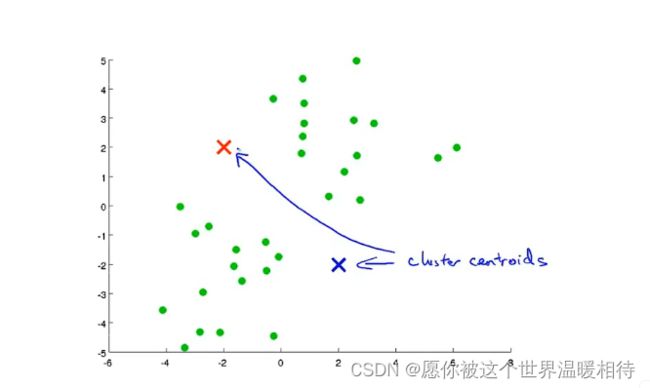
无监督算法相对于监督算法，其输入数据是无标签的，如下图所示，只是知道有这么一些数据点

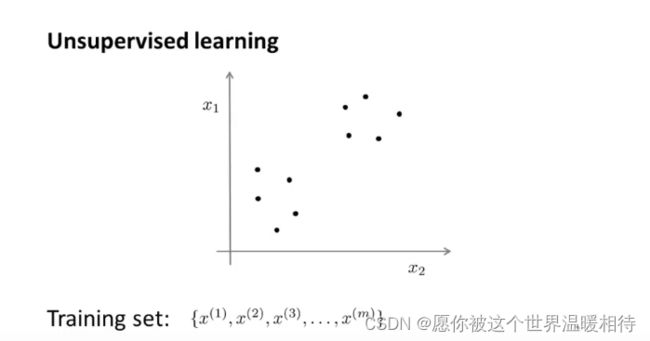
找到一些隐含在数据中的结构，通过这些结构可以使得算法将数据分为不同的聚簇，如下是分成了两个部分，生成不同的蔟的算法，称为聚类算法

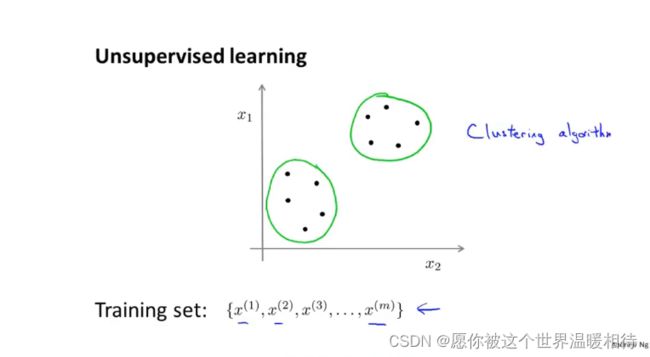
无监督算法可以找到其他类型的结构或者数据的其他类型的模式，而不单单是聚簇算法

K-means算法（K均值算法）

原理

一种聚类算法，是一个迭代算法，他还会做两件事，一是蔟分类，二是移动聚类中心

首先随机生成两个点，这两个点叫做聚类中心，并进行蔟分类

所要做的是，遍历样本，然后按每个样本离两个中心的距离，离谁近就分配给谁

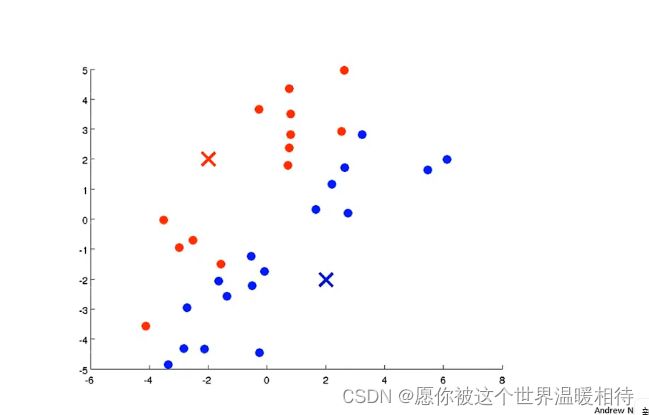
第二步是移动聚类中心，两个聚类中心，将其移动到同色的点的均值处，也就是例如统计所有样本，并计算出其均值，红色点的聚类中心移动到该点，同样的蓝色的聚类中新也同样，如下已经是移动到新的位置上了

然后重复上述两个步骤，也就是第一步是根据点离两个中心的远近将其分配给最近的聚类中心，然后在进行移动聚类中心，过程不断进行迭代。迭代结束的标志是，聚类中心不再改变了，此时我们可以说k均值已经聚合了

具体算法

参数输入

K-means算法中，输入存在两个参数

• 第一个参数是K表示最后要形成的聚簇的数量
• 第二个参数是输入的训练集，因为是无监督算法，所以没有具体的y值

其中x⁽ⁱ⁾是一个n维实数向量，而我们按照一般规定是不考虑x0的，所以训练集一般是n维实数向量

如下是对上述步骤的算法描述，首先是随机初始化k个聚类中心u1…uk

使用c⁽ⁱ⁾表示第1到m各样本最接近的聚类中心，其中聚类中心的表示是使用他所对应的下标进行标记

第二步是遍历1到k，将聚类中心，也就是uk更新为接近他的样本的均值处

如果存在一个聚类中心周围没有任何的点，那么可以选择直接移除该聚类中心，这个时候你最终得到的聚簇就会变少，如果你真的需要输出原本设置的聚簇的数量，那么可以使用将这个没有任何点的聚类中心进行重新初始化

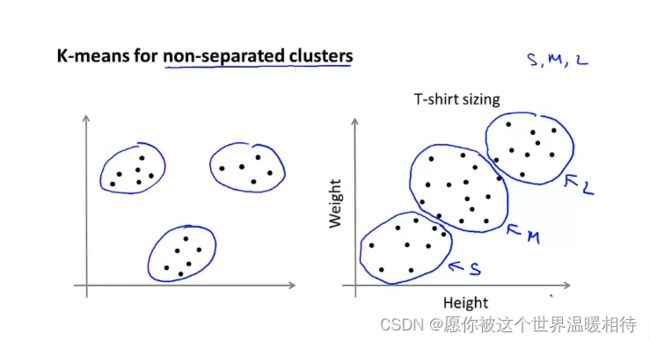
用于分离不佳的蔟的问题

如下左图中，是很明显分成了多个聚簇，但是像右图的情形中，就不是一种很好的分类，这是一个关于T-shirt的例子，得到的身高于体重的相关的数据，但是K-means算法是还是会将他分为多个聚簇，如下的三个圈，从小到大可以表示小号，中号，大号三个码的衣服，适合不同的人群的需求

K-means算法的一个优化目标函数

相当于用于K-means最小化的代价函数，他的作用：

• 可以让我们对学习算法进行调试，确保k-measn算法运行正确
• 可以帮助k-meas算法找到更好的蔟，并且避免局部最优解

如下是K-means的代价函数，这个代价函数有时候也叫失真代价函数或者K-meas算法的失真，主要二者的距离有关

如何初始化K-means算法

该算法的第一步是随机初始化K，并得到K个聚类中心

事实上有多种方法可以用来随机和初始化聚类中心

如下是一种表现比较好的随机初始化方法，首先应该保证聚簇的数量K小于训练集的样本的数量，然后从训练集中挑选出K个样本，并作为聚类中心，如下由上图是比较理想的状态，在初始选择K=2的情况下，分类在两个视觉上明显分类的聚簇上各自挑选了两个点

按照上述的方法，K-means可能随机选择如下右下角的图中的情况，这种情况也是被允许的，但是效果可能不会很理想

随机的初始化状态不同，会使得最终的K-means算法的产生蔟有所不同

K-means的局部最优解

因为随机初始化的效果可能会出现不理想的状态，那么会造成右下角的情况，部分聚簇的分到的样本比较少

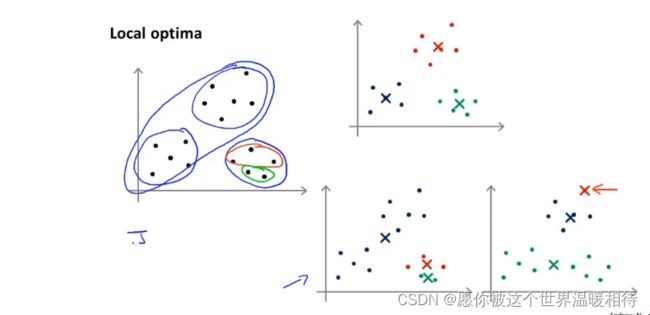
局部最优解指的是代价函数J的局部最优解，如上的右下角的情形，就是除以局部最优解的情况，不能很好地最小化代价函数J

如果想达到右上角的图像中比较好的情况，可以进行尝试多次初始化，具体如下，多次运行算法，并计算其中的代价函数的值，并找到最终代价函数值最小的组合

使用如下方式，可以在K选择非常小的情况下是一种比较好的饭方式

K-means如何选取聚类数量K

聚类数量不容易选择，是因为在数据中有多少个类是不清楚的

“肘部法则”是一种用来选择聚类数量的方法

如下左图中是其过程，K从1开始不断增大，并求出对应分类的相对应的代价函数值的，这个过程中可能涉及到多次初始化，但是会随着聚类数量的增大而代价函数不断减小的情况

其中存在如下情况，在黑色箭头指向的K=3的点往后，随着K的值不断增大，代价函数的值下降速度开始减缓，因而K=3会被选择为当前训练集对应的聚类数量，整个函数图像就像是一个手肘一样，手肘的地方事实上是对应的拐点

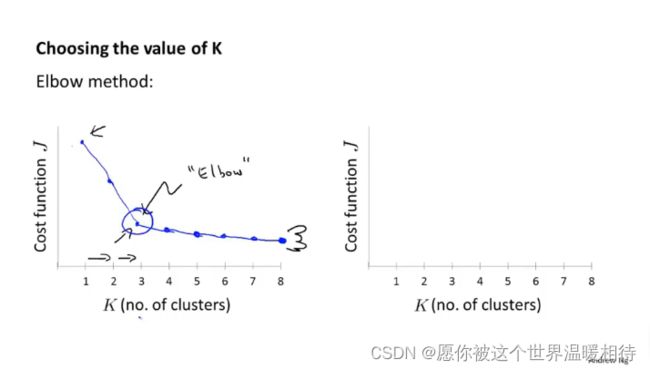
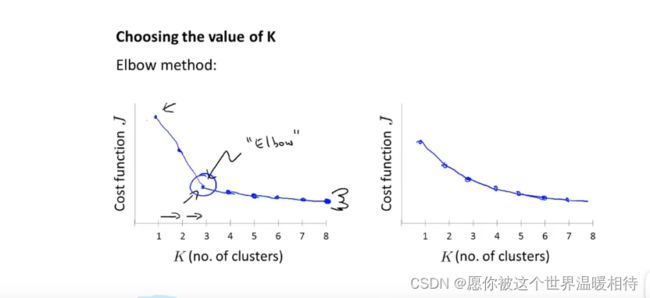
事实上：手肘法则并不被常用，因为其实际用到聚类问题上时，左图时比较理想的状态，往往最后会得到一条模糊的曲线，并不能看出拐点，如下右图，在这种情况下选择拐点是十分困难的

因而肘部法则是一个可以尝试的方法，但是并不能解决任何问题

有时候，你用K-means算法是为了某种目的，具体情况具体分析，在选择聚类的数量单时候可以基于如何让K-mens更好为你的后续目标进行服务是一个作为一个基本的准则

降维

为什么需要降维以及降维的应用

• 数据压缩：数据压缩不仅能让我们对数据进行压缩，减少数据占用的内存或硬盘空间，它还能让我们对学习算法进行加速
• 数据可视化吧

二维转一维

现实应用中，数据可能来自不同的源，对于某个度量可能会是不同的特征，比如两个地方给来的特征中，对长度这个特征进行描述，其中一个使用的是英寸，而另一个组使用得到是厘米，二者是高度相关的，如果特征高度相关，那么就会产生冗余的情况，那么这个时候就需要降维

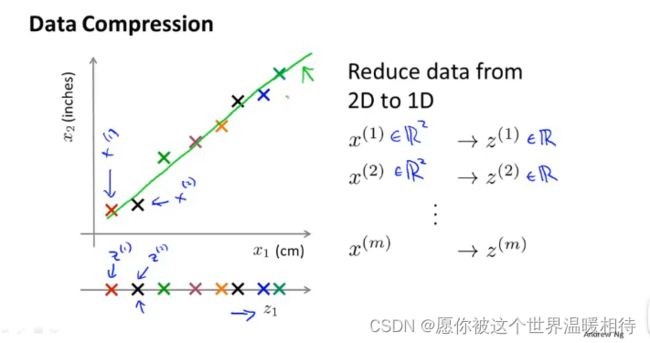
如下例子，假设某个训练集中存在多个特征，这里去除两个特征，如下其中一个特征是英寸值的长度，另一个特征是厘米值的长度，二者是高度相关，也就是存在高度冗余的情况

处理这种情况，可以进行拟合一条直线，使得样本尽量落在该直线上，然后对于不在直线上的样本，可以进行投影到直线上，形成对应样本的近似样本，最终这些近似的样本全部落在一条直线上，如下图所示

使用z⁽ⁱ⁾进行表示投影后的新特征，同样表示被投影的样本的近似样本。因为在一条直线上，那么就成功将二维的特征量转变成一维度，从而达到减少冗余的目的，并且可以使用一个实数去唯一在直线上找到对应的样本

三维转二维

实际上可能存在10000维，然后进行进行降维到100维的情况，如下维了更好地展示具体的过程，这里使用的是三维转二维

三维降低到二维的方法类似上述，可以将三维的点投影到二维的平面上（这个平面不一定是x1和x2相对应的坐标轴形成的平面，可能是在半空悬浮的一个平面），并且要定位投影后的新特征，需要两个数进行定位，这里使用的是z1和z2，如下右下图所示，这里就相当于上述二维降一维的时候使用的z1进行定位样本的方式

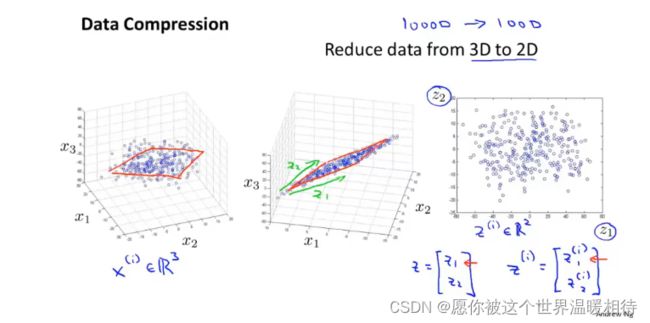
可视化

如下是不同国家的不同的特征，包括50个，当进行可视化的时候，50个特征显然是不理想的，那么是否可以使用两个主要的特征进行表示这些样本的情况？

这个时候我们可以考虑使用两个特征量来表示这50个特征，然后再进行可视化。因而对于这个问题，实际上就是要解决如何将这50个特征转化为两个特征变量表示

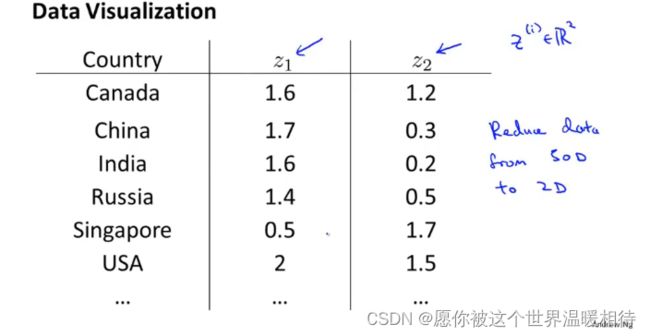
如下可以将50个特征值偏向如下两个主要特征，进而用于进一步评估和检查数据，其中z1表示的是GDP，z2是个人GDP

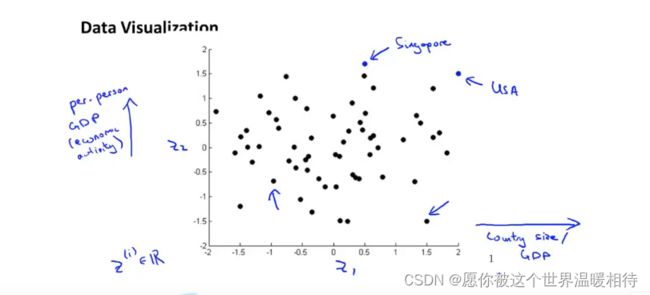
主成分分析方法（PCA）算法

原理

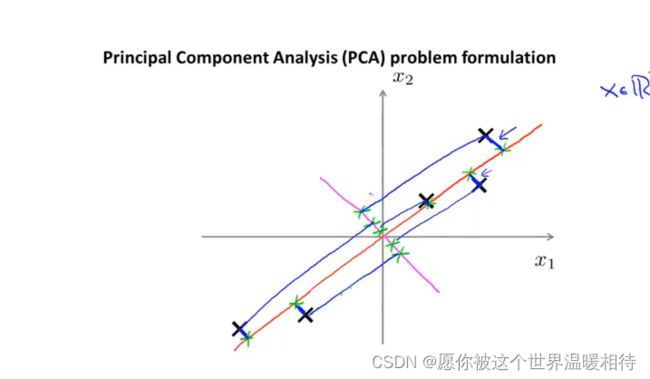
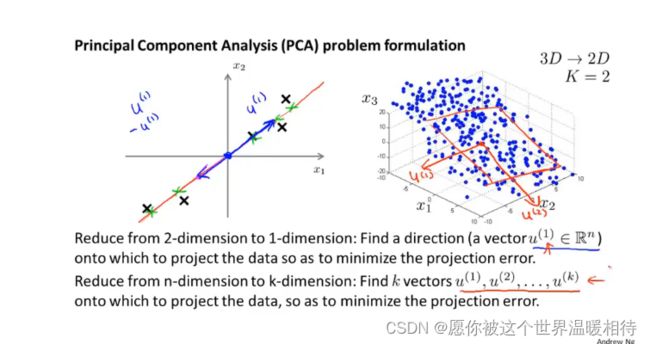
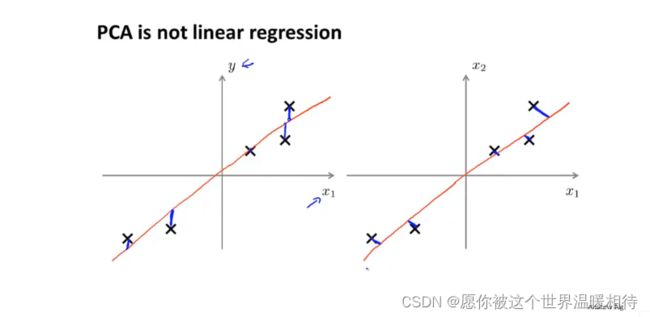
PCA的作用是找到一个低维的平面，然后将数据投影到上面，并且投影的距离的平方最小，如下蓝色的线段，该线段表示的距离有时候也称为投影误差，PCA就是要使得投影误差最小，如下

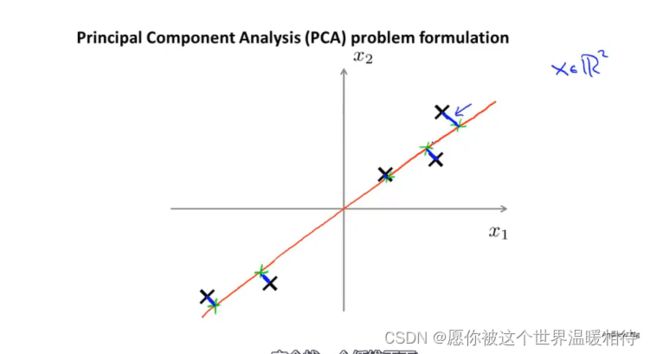
首先进行均值归一化和特征规范化，使得特征量x1和x2其均值为0，并且其数值在可表的范围之内

他需要左的是最小化样本到投影平面的距离，如下橙色的投影平面将会被作为PCA的选择而不是红色线，因为样本在红色线上的距离比较大

如下左图就是上述的例子，是要从二维转换到一维的状态，所以需要找到一个方向向量u1，然后将所有的样本都投影到该方向向量上，该方向向量无所谓方向，只要是同一条直线就行了，如下左图拟合的直线

如下右图是，是三维转换成二维，那么就需要两个向量u1和u2，然后然后空间中的样本投影到由这两个向量组成的平面上

更一般地，要将n维平面降维成k维，那么就需要k维向量，并且对于空间中的样本具有k个方向，例如上述二维转一维，这个时候只有一个方向，就是直接投影到直线上的方向，而三维转二维的时候需要考虑两个方向，最终是投影到平面上

总的而言，PCA就是要找出能够最小化投影距离的方式来对数据进行投影

PCA在二维转一维的时候有点像线性回归拟合的直线，但事实上二者不相同，如下左边是线性回归拟合的直线，他要做到是预测值的输出尽量接近事实上的结果y，因而考虑的是相对于整体的垂直距离，而PCA是考虑的投影的代价，考虑的是样本到投影平面的垂直距离而不是全局的

并且在PCA中，所有的元素都是同等的，并没有特殊的变量y，而在线性回归中，所有的样本x都是为了输出预测值而服务

过程

• 使用PCA之前，首先要做的是进行数据预处理，首先是执行均值标准化
• 然后PCA要解决的问题是就是如何找到投影向量，如上述二维转一维的时候，PCA需要找到u1向量，而在三维转二维的时候，需要找到u1和u2两个方向向量
• 然后是如何得到表示投影后的数值，如二维转一维中，在向量u1上，对应样本的投影可以使用z1…zn进行表示，也就是使用一个实数表示了对应的样本，实现了降维

均值标准化

首先计算每个特征的均值，然后用xj-uj（uj为对应的特征的均值）去代替xj，这将使得每个特征的均值正好为0

如果不同的特征有非常不同的范围，我们也可以将具体的特征缩放到可比较的范围，如之前监督学习中的房价在0到2000的范围，而房间的数量在0到5的范围，使用使用如下均一化公式，其中sj表示一定的测量值，而该值经常使用标准差

寻找投影向量u_n

在数学上该过程比较复杂，这里简单进行描述一下应用过程

将n维降维到k维，首先要计算协方差矩阵，下边的符号称为Sigma，外形类似求和标志，他是一个矩阵，并且是一个n*n的矩阵，因为从如下公式中，x⁽ⁱ⁾是一个n1的矩阵，那么他的转置矩阵就是1n，那么二者进行相乘，就会得到n*n的矩阵

协方差矩阵总是满足数学上的一个性质叫正定矩阵

初始化协方差矩阵如下，可以对各个位置进行展开为u⁽¹⁾…u⁽ⁿ⁾，最终就是一个n*n的矩阵

而我们需要将n维降维为k维，那么我们需要的就是提取前k个向量，然后进一步处理处k个向量，这就给了我们k个投影方向，也就是我们想投影数据的方向

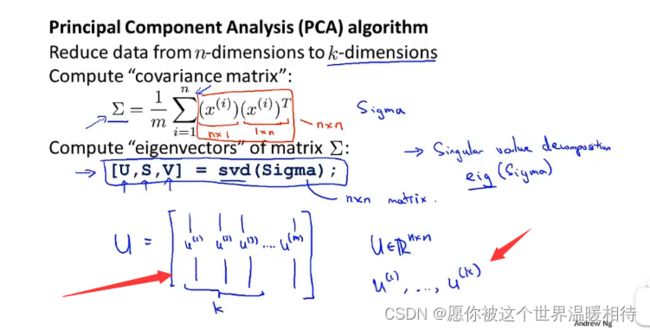
要提取矩阵u的前k列并最终形成k个向量，首先是获取获取U矩阵的前k列，最终得到一个nk的矩阵，可以叫他u_reduce，我们将用他对我们的数据进行降维

而对实数z的计算实际上时等于u_reduce的转置相乘样本x

提取后的矩阵是nk矩阵，其转置矩阵是kn维矩阵，而x是n1的矩阵，二者相乘是k*1的向量，最终得到的z是k维向量

应用PCA

应用PCA加速学习算法，我们经常使用PCA对监督学习算法进行加速

如下当输入的x⁽ⁱ⁾的特征量的数量非常庞大，例如输入一个图像的信息，这个时候应用逻辑回归或者是支持向量机或者神经网络都会使得效率非常慢，但是我们可以通过PCA降低数据的维度，从而使得算法的效率提高

具体步骤是提取输入，这个时候相当于一个无标签的数据，然后将数据通过PCA算法进行降维处理，并将处理后的数据作为新的输入

对x⁽ⁱ⁾与z⁽ⁱ⁾之间的映射，我们应该是指在训练集上运行PCA得到，并且相关的参数也是如此，例如u_reduce这些参数，以及进行特征缩放以及均值归一化等等都应该在训练集上得到，在找到所有的参数后，可以把这个映射用在交叉验证集或者测试集的其他样本中

总的来说，PCA仅仅在训练集中的数据上运行，不能在交叉验证集以测试集上，在定义到了x到z之间的映射后，可以应用这个映射到交叉验证集以及测试集上

错误应用PCA

用于过拟合

在解决过拟合问题一种方法中，可以通过减少特征量进行处理。这里一个错误的做法就是使用PCA进行防止过拟合

因为PCA本质上时值关心输入的特征x⁽ⁱ⁾而不关心具体的输出y，因而在进行降维的过程会丢失一些关键的数据，最终使得丢失掉一些有价值的信息

而使用正则化的方法，是添加了正则项，但是并没有对y的输出，也就是说正则化以后也是与y紧密关联的

因此使用PCA最好的方式是用他来提高学习效率，但是不应该使用PCA去防止过拟合，而是使用正则化

不加思考使用PCA

对于是是否使用PCA进行加快学习效率或者对数据进行压缩，应该有充分的理由，如果没有充分的理由，最好是使用原来的数据而不是不假思索地使用PCA

压缩重现

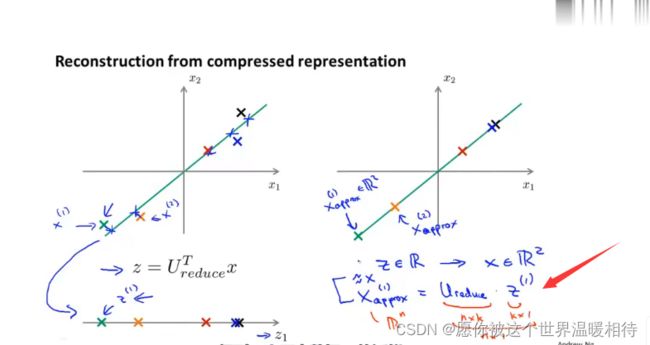
上述降维是高维特征量转变成低维特征量，这是压缩，那么是否能从低维的新特征量重现高维特征量的近似值

上述过程中，实数z=u_reduce*x，那么反过来求原来样本的x的近似x_appro = u_reduce·z

异常检测

用来检测一个新的样本是否存在异常

什么是

在给定数据集，对给定训练集进行数学建模，即得到p(x)，也就是我们将对x的分布概率建模，其中x是这些特征变量

然后进行测试新样本，如果输入的新样本低于某个阈值，将会把该样本标记为异常

应用实例

• 欺诈检测：根据用户在网站上行为，例如登录的次数、访问网站的次数等等特征进行数据建模，然后再低于阈值的时候进一步进行检查用户的档案，从而让你的网站方法欺诈行为
• 使用在制造业上，检查产品的是否正常
• 数据中心的计算机监控：获取计算机集群中的某些特征，例如温度、CPU负载等信息进行数据建模

构建异常检测算法

构建过程

我们处理异常的方法是用数据建立概率模型p(x)，我们要试图解决处哪些特征量出现的概率比较高，哪些特征量出现的概率比较高

我们将利用具体的特征x1…xn进行建模

当x1…xn都服从正态分布的时候，可以在如下建模相关公式I填入状态分布相关参数，最后等式是一个累乘的符号

上述过程总结如下

• 首先是选择可以指出异常特征，然后拿到具体的训练集
• 对训练集中每个具体的样品特征进行统计其均值u以及方差σ²
• 在利用正态分布相关参数进行数据建模得到p(x)，最终得到关于正态分布函数的概率密度的相关项的累积
• 进行判断是否异常通过阈值ε

分布项p(x)的估计问题，有时候也称为密度估计问题

应用案例

如下左下图的图像是在p(x)与x1、x2的三维图像，p(x)的值，根据上述公式，就是右图中两个与x1、x2相关的p相乘的结果

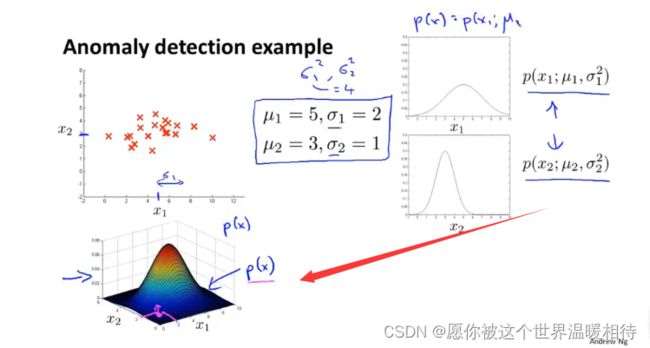
如果存在一个待测试的样本x_test，那么就可以将这个样品的特征向量传入到p(x)中，然后通过上述公式对比阈值ε，至于ε如何得到，在接下来的部分会提及

评估一个异常检测算法

评估流程

进行评估可以判断添加某个特征对算法是好还是坏，然后再决定是否要纳入这个特征，这可以帮助我们更好为一个开发一个学习算法做决定

假设我们有一些有标签数据，这些标签数据主要包括有异常样品以及无异常样品，其中使用y=1表示有异常，而使用y=0表示无异常
我们可以整合出一个训练集，其中训练集进包括无异常样本或者是有异常样本，在训练集中，仅仅使用上述的有标记标签的输入部分，也就是相当于无标记标签，使用训练集的函数进行拟合p(x)
然后定义一个交叉验证集以及测试机用来评估这个异常检测算法，这些数据都是有标注的标签，在这些数据中，我们集中包含有异常的样本，这些样本是已知是有异常的

如下是使用上述过程进行推到和评估检测算法

• 首先是通过无标签的训练集（实在有标签基础上提取出来的输入特征向量，并且主要包括某一类的样品，如正常的样品或者是异常的样品）进行拟合p(x)
• 然后输入到交叉验证集中，这里使用检测最终输出的分类结果作为具体的指标是不理想的，因为交缠验证集中，正常的样本将会占用绝大多数，这就类似于之前的偏斜类，当我们异常检测算法只是对y=0预测输出，同样会的得到一个比较好的结果，但是并不是一个好的算法，而且有故意倾向。这种情况我们可以使用查准率/召回率（Precision/Recall）进行计算F1，最终进行评估算法在交叉验证集以及测试集中的表现
  

选择ε

ε是我们评估是否异常样品的阈值，我们可以通过交叉验证集进行选择

对于该值的选择，可以在交叉验证集进行不断测试，选择不同的ε的值，把使得F1-score值最高的ε的值作为我们的阈值

异常检测以及监督学习之间的选择

异常检测以及监督学习的过程有许多相似的地方，这里给出一些与他们相关的情况去选择什么时候使用异常检测还是监督学习

使用异常检测

1. 正常例子比较少，那么可以考虑使用一个异常检测算法。因为在异常检测算法中，你可以有较少的正样本以及大量的样本，可以在拟合所有的高斯参数的过程中，仅仅使用这些负样本，这样仍可以很好地拟合p(x)的值
   
   相反
2. 存在大量负样本
3. 存在不同的异常的情况，在这种情况下，很难从正样本中进行检查哪些是负样本
4. 未来可能会有其他异常样本我们目前并不知道的

使用监督学习

1. 对于监督学习，在合理范围内有大量的正常样本以及不正常的样本
2. 有足够的正样本例子，已知他们都是正样品，并且未来可能会有更多这些类似目前训练集的正样本输入到训练集中。这种情况使用监督学习能够观察大量正样本和负样本学习到相应特征，并且尝试区分正负样本

总的而言，就是对于少量的正样本的情况下，对于学习算法是不可能从这些正样本中学习到足够的知识，我们要做的是使用大量负样本，让这个算法学到足够多的内容，就是异常检算法从哪些负样本中学习p(x)的值。我们保留少量的正样本用来评估我们的算法，这个算法用于交叉验证集或者测试集

二者的应用场景举例

上述场景中，如果在正负样本量级相当于或者是有大量的正负样本的情况下，可以使用监督学习

设计或选择异常检测算法的特征

特征调整

异常检测算法是使用高斯分布进行数学建模的，在数据进入异常检测算法之前，我们可以通过直方图或者其他可视化方式进行确保数据呈现高斯分布的情况

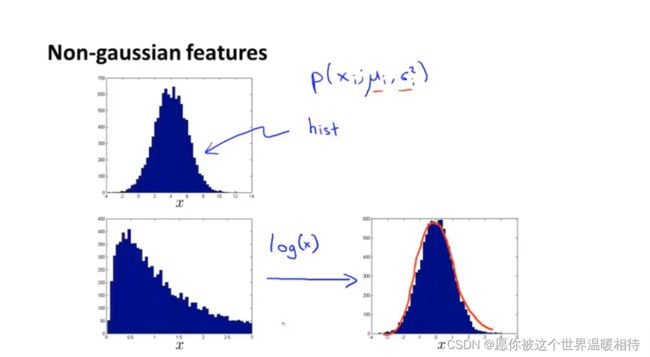
对于数据不是呈现高斯分布的情况，我们需要进行数据转换使得最终呈现出高斯分布的情况。虽然说将数据转换成类似高斯分布的情况也能正常运行，但是数据接近高斯分布可以让算法更好地运行

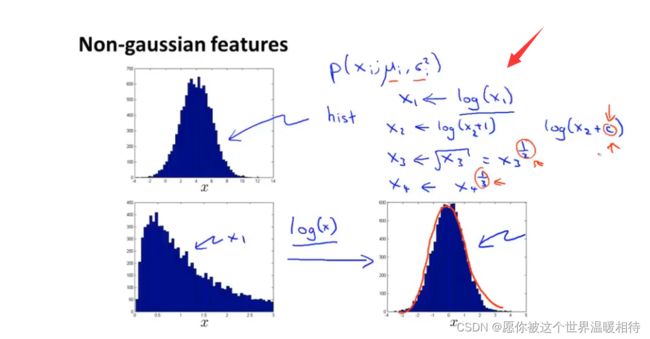
如下左下角的图中，对具体样本x进行log转换，也就是对每个样本x，都使用log(x)进行对数转换，最终转换成类似高斯分布的情况

也可以使用其他方式，例如开根等等进行处理

如何得到异常检测算法的特征

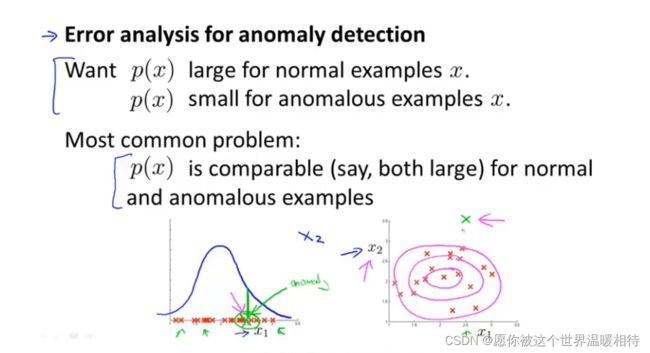
可以通过一个误差分析步骤，就是类似于监督学习部分的方法，在训练集上进行出模型，然后在交叉验证集上进行验证该模型，并根据结果统计预测错误的样本，综合分析其特点，例如可以跟其他正常样本进行比较，可以考虑添加新的特征进行调试，选择使得交叉验证集比较好的特征

如下左下图的是只有一维的特征量，绿色部分表示的是异常样本，但是算法并没有发现他，这个时候可以考虑添加特征x2，如右图所示，添加特征x2以后，异常样本离整体样本比较远，处于边缘状态，那么这个时候就可以进行更好地判断他是异常样本了

分析举例

如下例子中，应用场景是数据监控中心，其中包含多个特征x1…x4。假设在程序中出现了某句代码出现死循环，这个时候可以考虑x3和x4两个，因为当代码死循环会增加CPU的负载但实际的网络流量并没有增多，因而对于这部分的异常就可以进行考虑这两个特征，可以进行创建新的特征，如下的x5或者是x6

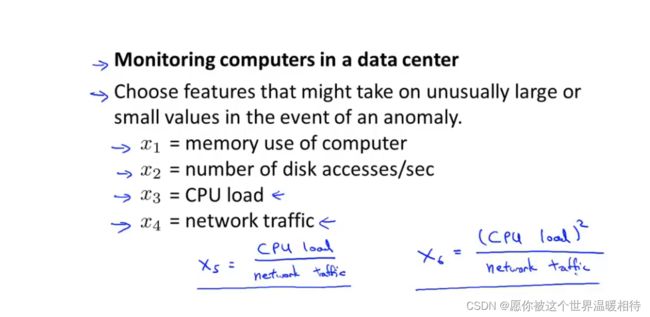
多元高斯分布

异常检测算法的一种可能的延伸，他能捕获之前的算法检测不出来的异常

存在问题

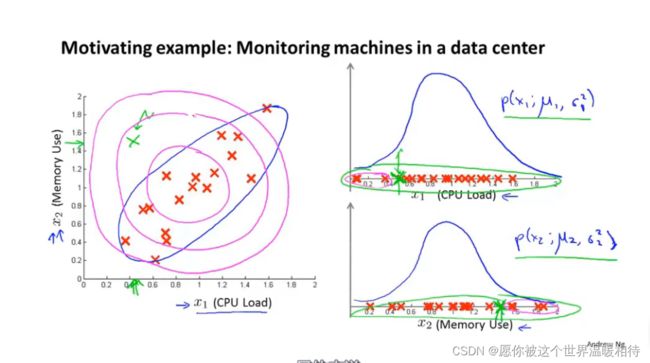
如下左图包含另两个特征，x1是cpu负载，x2是内存使用，图像中左上角的绿色点，是异常点，将异常点的两个特征分别在对应的特征上标记出后，可以看到其CPU利用率比较低，但是内存利用率比较高，但实际上这种情况也并没有显得特别异常

之前的异常算法中，会认为某一部分是正样品的概率比较高，例如如下左图中的同心圆，认为其中中心部分的存在正样品的概率比较高，因为从每个特征的高斯分布来看，该部分确实是分布最集中的，而根据两个高斯图像往外延伸，就是再向外的同心圆，这些部分被认为存在更低的概率是正样品

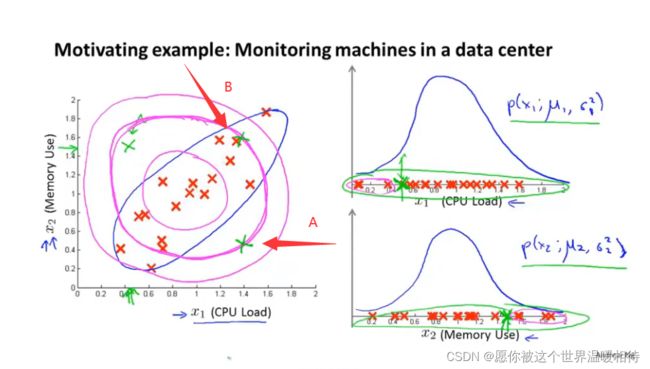
上述存在的问题是，他认为在一定的范围内存在相同的概率是正样品，如下A、B两个位置，是存在同样的概率是正样品，事实上A处是相对比较低的概率是正样品，不是A、B同概率

算法改良原理

多元高斯分布下的p(x)的建模

要对上述进行改良，就可以使用到多元高斯分布或者叫多元正态分布

使用多元高斯分布，不在对p(x1)、p(x2)进行建模，而是统一丢整体p(x)进行建模

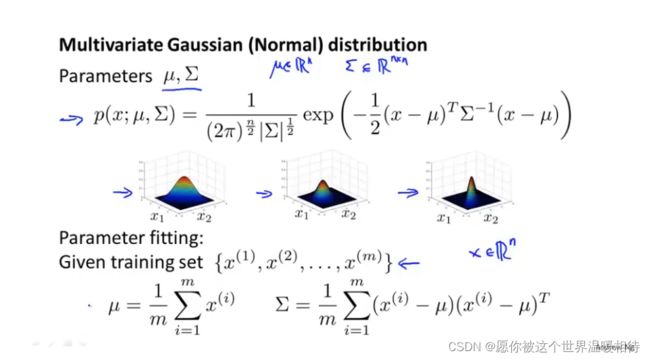
其中高斯参数μ是一个n维实向量集，而协方差方程∑是一个n*n矩阵。最终对整体建模有如下公式

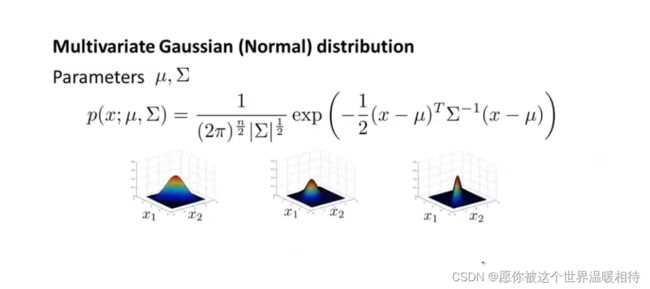
## 多元高斯分布下p(x)的可视化举例

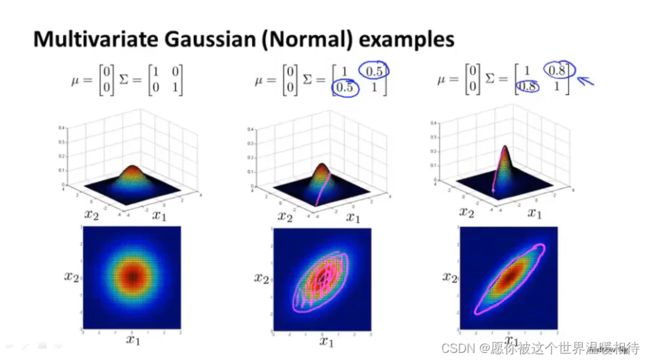
如下只是存在x1、x2两个特征，在主对角线上，左上角是x1的方差，右下角是x2的方差，改变他们的值会有如下表现

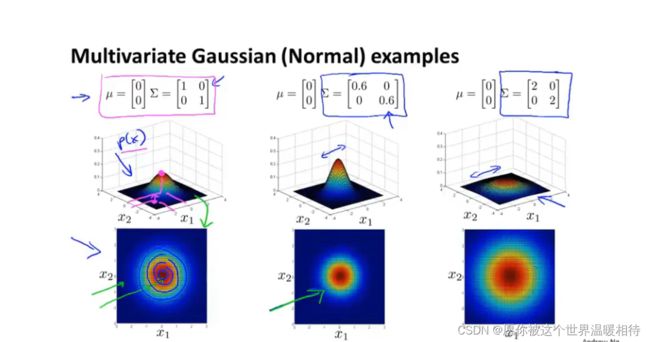
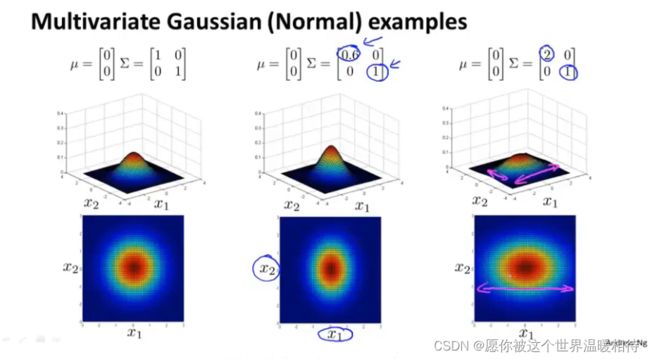
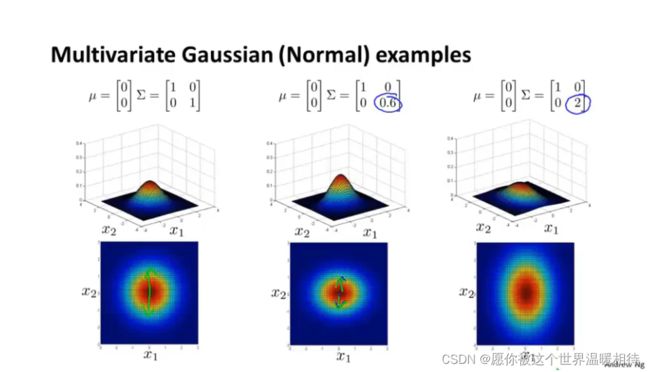
你可以它给的数据的相关性建立模型，我们可以用他来给x1和x2高度相关的情况建立模型

如果你改变协方差矩阵中的副对角线上的元素，你会得到一种不同的高斯分布

当使用负值的时候将会得到负相关的情况，最终使得大多数元素都落在x1和x2负相关的区域上，也就是x1=-x2，而不是x1=x2

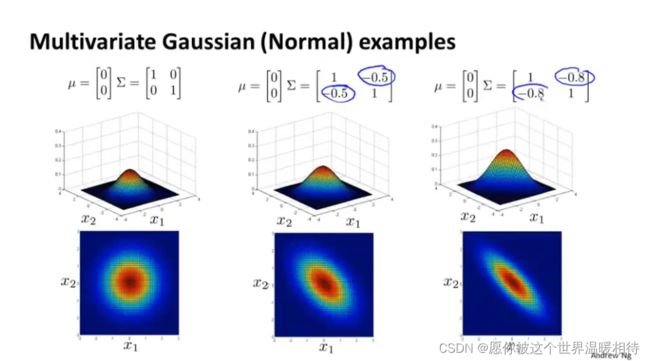
u向量包括了各个特征的均值，如下，第一个参数x1的均值，第二个参数x2的均值

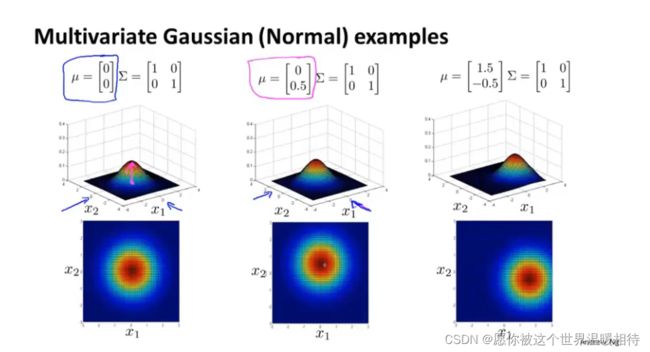
多元高斯分布能够捕捉到不同的分布，他最重要的优势就是能够让你描述两个特征变量之间可能存在正相关或者负相关的情况

多元高斯分布应用于异常检测

参数拟合

对于多元高斯分布，有两个参数μ和∑，对于估计二者的方法如下：通过具体的符合多元高斯分布的训练集

工作原理

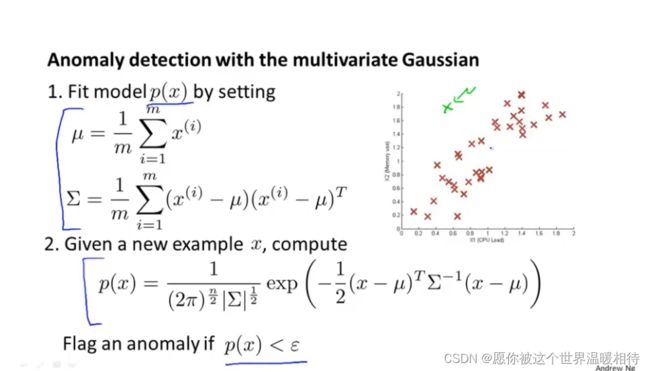
如果将高斯分布拟合到数据中就能得到如下情况，对于越往内部的范围是正样品的概率越高，而不是上述中在一个更大的范围

多元高斯分布模型和原始高斯分布模型的关系

原始高斯模型如下

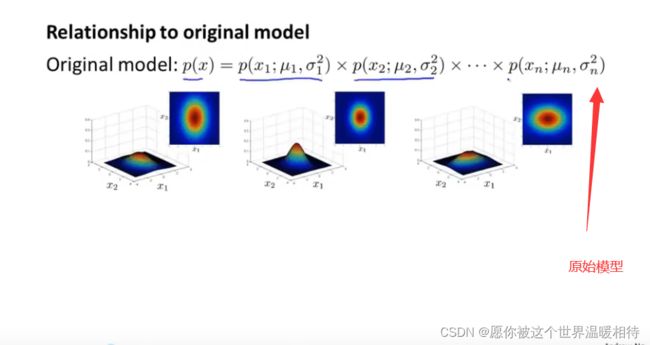
多元高斯分布模型与原始模型之间的一个区别是：多元高斯分布模型的轮廓（等高线图）总是轴对齐的

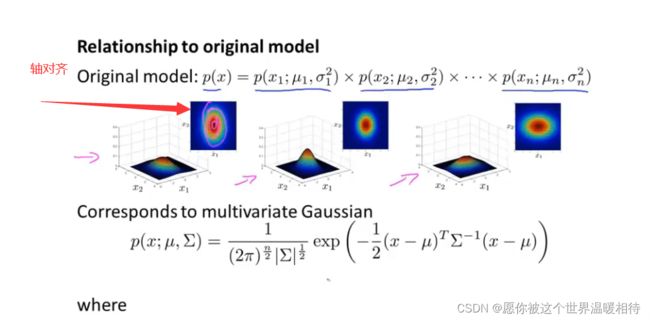
原始高斯模型实际上特殊情形下的多元高斯分布，这个种情况是，其协方差矩阵中，主对角线上是每个特征量的方差，而其他部分都是0，这个时候两个模型是完全相同的

在这种情况下，可以使用原始高斯分布模型或者是多元分布的模型

原始高斯分布模型和多元高斯分布模型如何选择

多元高斯分布模型在捕捉特征之间的关系中有着很多的优点

使用原始高斯分布模型

1. 在异常检测中，当使用异常特征的组合去创建新的特征检测异常的时候，如之前的大数据中心的例子中，两个异常特征是CPU特征x1以及内存利用率x2，那么就可以创建新的特征x3，x3=x1/x2用来作为异常检测项，进而捕获更多相关特征
2. 在特征量的数量比较大的时候，能适应数量巨大的特征，使得整体计算成本更低
3. 可以在训练集的数量比较少的情况下发挥作用

使用多元高斯分布模型

1. 多元高斯函数能够自动捕捉这些不同特征之间的关系，这能让你省去创建额外的特征（一些能用异常的组合值来体现的特征）
2. 适合n值的范围比较小的，计算成本比较高，因为其中协方差矩阵是n*n的矩阵，并且需要求出其逆矩阵，这种情况在n非常大的时候就会增大计算成本
3. 必须保证训练集的样本数量m>样本的特征数量，如果不是的话，协方差矩阵就会是不可逆的，最终使得多元高斯分布不可用。一般而言当m远大于n，并且n比较小 的情况下才使用多元高斯分布模型

如果在使用多元高斯分布模型的时候发现协方差矩阵不可逆，其中一个问题就是训练集的数量m小于n，还有一个原因是存在冗余的特征（高度相关的特征，在线性代数中，就是特征之间是线性相关的）

要解决解决这个问题，首先确保m远大于n，然后检查是否有冗余特征