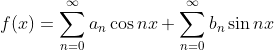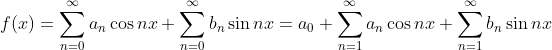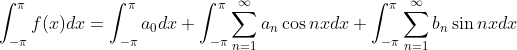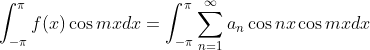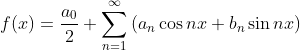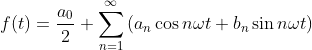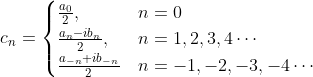傅里叶级数与傅里叶变换
一、Games101 中出现的傅里叶变换(FT)的简单推导
到底什么是傅里叶变换:它的物理意义是什么,公式又从何而来?
以下的内容出现在 Games101 中的第八章:光栅化(深度测试与抗锯齿)
中,课程中这一部分大致介绍的内容是
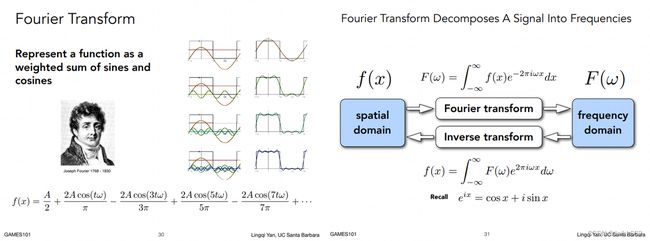
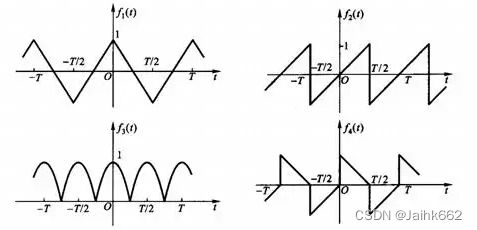
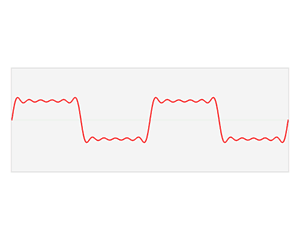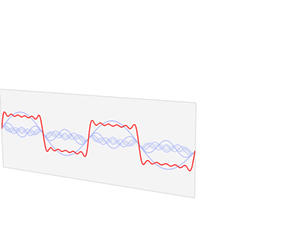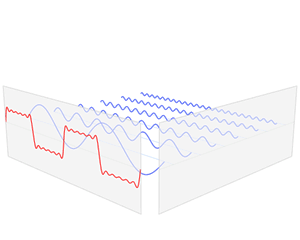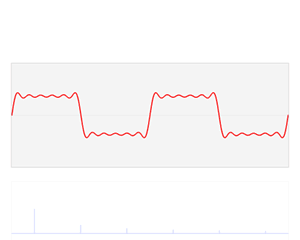
任何周期函数 ![]() 都可以分解为无数个不同频率、不同幅值的正、余弦信号。和泰勒展开一样,这也是一种函数展开/逼近方案:即傅里叶级数展开,其中左边那一张 PPT 就是一个简单的例子
都可以分解为无数个不同频率、不同幅值的正、余弦信号。和泰勒展开一样,这也是一种函数展开/逼近方案:即傅里叶级数展开,其中左边那一张 PPT 就是一个简单的例子
右侧则为傅里叶变换及其逆变换:它和傅里叶级数展开的概念是非常相似的
如果不了解傅里叶变换(FT),可能会对视频中右边突如其来的内容非常陌生,只知道它用于将一个函数变成另一个函数,但是这个式子是怎么推导的,具体是什么变成什么可能就没有太多头绪
而这一章的内容,主要就是对上面内容的答疑解惑
1.1 前置1:三角函数系
三角函数系即包含所有不同周期的三角函数的集合
![]()
其中三角函数拥有一个非常重要的性质:正交性
和向量垂直内积为0一样,两个函数内积 ![]() 即两个函数正交,而对于上面的两个特例:即 m = n 的情况,其积分结果为
即两个函数正交,而对于上面的两个特例:即 m = n 的情况,其积分结果为 ![]()
正是依赖这个特性,后续才可以任意函数中分离出指定频率的波形
1.2 前置2:三角函数的指数表示
3Blue1Brown 有一个视频很好的介绍了
到底表达了什么,如果有兴趣的话可以直接去看:【官方双语】微分方程概论-第五章:在3.14分钟内理解e^iπ,搞懂这个之后,这一部分就可以直接跳过了
虚数 i 这个概念基本上只要上过高中的都知道,只不过大多数人对它的印象只剩下了一个公式 ![]() :其余的就都不记得了,那么乘以虚数的意义又是什么呢?
:其余的就都不记得了,那么乘以虚数的意义又是什么呢?
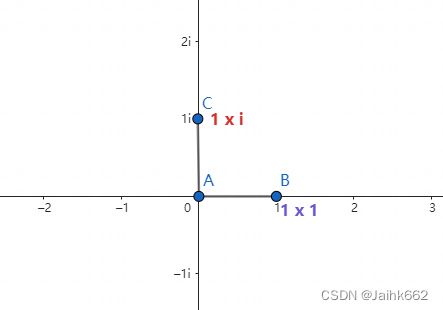
如上图有三个线段线段,线段 AB 的长度是1:当它乘以2的时候,它的长度发生了变化,拉伸成了线段 EF,而当它乘以 -1 的时候,就变成了线段 CD,或者说代表着原线段在数轴上围绕原点旋转了 180°
既然乘以 -1 相当于旋转 180°,考虑到 ![]() ,那么是不是就可以理解为:乘以 i 就是旋转了 90°?
,那么是不是就可以理解为:乘以 i 就是旋转了 90°?
是的,不过到此如果只考虑一维的实数轴就不够用了,因此我们可以加一条垂直的虚数轴已构成一个复平面,这样我们就可以把虚数乘法也表示出来:即乘以实数表拉伸,乘以虚数表旋转
但是到这里还没有结束,要知道本章之所以要提到虚数 i,主要是为了解释后面出现的 ![]() ,以及经典的欧拉公式
,以及经典的欧拉公式 ![]() ,可能就算你理解了虚数乘法,也未必能理解虚数作为指数意味着什么
,可能就算你理解了虚数乘法,也未必能理解虚数作为指数意味着什么
一个事实是:其实很多时候某些东西单独看是没有意义的,只不过为了实现一些目的,我们后来的人们手动赋予了它意义,尽管你完全理解不了:是的它就是一个定义,数学家就是这么理解它的(当然其一定是有依据的,而不是乱来)
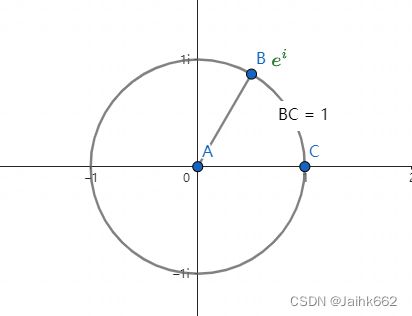
而虚数作为指数就是这么被“定义”出来的,其实它已经和正常我们理解的指数完全不是一个概念了,也就是说我们不能说 ![]() 就是连续 i 个 e 相乘,它是错误且没有意义的,事实上,它表达的是下面这个东西:
就是连续 i 个 e 相乘,它是错误且没有意义的,事实上,它表达的是下面这个东西:
即 ![]() 表示为单位线段旋转一定角度,这个角度对应的弧长为1,这个定义是根据复导数
表示为单位线段旋转一定角度,这个角度对应的弧长为1,这个定义是根据复导数 ![]() 反推出来的,当然具体细节就不再展开,有兴趣的话可以本节看上面引用的视频
反推出来的,当然具体细节就不再展开,有兴趣的话可以本节看上面引用的视频
知道这个后,两个著名的公式其实就不难理解了,你也可以瞬间化为数学家去把它们推出来:
后面主要会用到的,其实就是的下面的公式
1.3 傅里叶级数的推导
好了,可以回来了前面的内容:任何周期函数 ![]() 都可以分解为无数个不同频率、不同幅值的正、余弦信号,不妨可以先考虑最简单的情况,也就是先保证
都可以分解为无数个不同频率、不同幅值的正、余弦信号,不妨可以先考虑最简单的情况,也就是先保证 ![]() 周期
周期 ![]() ,即
,即 ![]()
,其中 ![]() 和
和 ![]() 都为常数项,然后有意思的就来了:有了这个级数表示,我们能不能得到一个左侧为
都为常数项,然后有意思的就来了:有了这个级数表示,我们能不能得到一个左侧为 ![]() 的等式呢?
的等式呢?
当然是可以的,就利用上面的三角函数的正交性求积分即可:
先计算最简单的 ![]() :
:
两边积分有:
根据三角函数的正交性,可以知道后面两项看上去复杂,其实都为0,也就有:
好了,到此结果显而易见了
接下来用同样的方法计算 ![]() :不过这一次我们在两边同时积分之前,先全部乘上
:不过这一次我们在两边同时积分之前,先全部乘上 ![]()
一样根据三角函数的正交性,第一项和第三项为0:就有
并且当前仅当 n = m 时,右侧的积分结果不为0,也就是说
游戏结束,关于 ![]() 的计算同理
的计算同理
好了,到此就可以得到一个最基础的傅里叶级数形式:
对于满足周期 ![]() 的
的 ![]() ,
,![]() ,有:
,有:
其中:
![]()
1.3.1 任意周期函数的傅里叶级数
前面考虑的 ![]() 周期满足最简单的
周期满足最简单的 ![]() ,现在在理解了上面内容的基础值之上,可以考虑去推导任意周期的通式
,现在在理解了上面内容的基础值之上,可以考虑去推导任意周期的通式
考虑周期 ![]() ,L 为任意值,也就是
,L 为任意值,也就是 ![]() ,那么就可以用换元法:
,那么就可以用换元法:
那么此时就只需要把 ![]() 带入到前面的级数推导中,就可以得出任意周期函数的傅里叶级数形式:
带入到前面的级数推导中,就可以得出任意周期函数的傅里叶级数形式:
其中:
1.3.2 傅里叶级数的复数形式
好了转折点来了,现在我们把前面第二节的欧拉公式拿过来:![]()
这个依旧是可以逆推得到(因为离本章的主题比较远,这一部分的详细推导就略了)
到这你会发现,其实这三个求和公式对应的区间加在一起正是负无穷到正无穷,并且它们的项都是 ![]() ,只是系数不同而已,因此可以直接将这三项整合起来得到:
,只是系数不同而已,因此可以直接将这三项整合起来得到:
其中:
好了,到此就只剩下最后一步了:那就是把前面 ![]() 和
和 ![]() 的结果代进去,就有
的结果代进去,就有
仔细看,右边像不像欧拉公式 ![]() ?此时配合奇函数偶函数的积分性质,就可以得出
?此时配合奇函数偶函数的积分性质,就可以得出 ![]()
而对于其它情况例如 ![]() 的推导,你也会得到一个完全相同的结果,可以说是非常的妙,到此为止,我们就得到了一个完美的傅里叶级数复数形式:
的推导,你也会得到一个完全相同的结果,可以说是非常的妙,到此为止,我们就得到了一个完美的傅里叶级数复数形式:
对于周期为 T 的函数 ![]() ,有:
,有:
通过等式①,我们可以对一段函数进行滤波,把指定频率的波段/信号给筛出来
1.4 非周期函数傅里叶变换推导
休息一会再来,前面对于 ![]() ,我们求得了他为周期函数情况下的傅里叶级数展开,现在尝试求出真正的“通解”:即任意
,我们求得了他为周期函数情况下的傅里叶级数展开,现在尝试求出真正的“通解”:即任意 ![]() 的傅里叶变换
的傅里叶变换
照应开头,主角要登场了!
1.4.1 时域与频域
这里强烈推荐一篇文章:傅里叶分析之掐死教程(完整版),里面关于频域与时域的介绍非常形象,并且和本文长篇的公式推导不同,里面基本不含任何复杂的数学公式,如果看多了 LaTex 换个心情也是可以的
还是那个周期为 T 的函数 ![]() ,如果我们画出对应的函数图像,横轴为 t,纵轴为
,如果我们画出对应的函数图像,横轴为 t,纵轴为 ![]() ,那么这个图像就是标准的时域图像,其中横轴变量 t 就代表着时间(Time)
,那么这个图像就是标准的时域图像,其中横轴变量 t 就代表着时间(Time)
然后就是傅里叶级数:
对于第②个式子,真正能决定最终函数结果的其实是其中的系数 ![]() ,而后面的
,而后面的 ![]() 其实是一种规则,代表着不同频率的波
其实是一种规则,代表着不同频率的波
因此,有另一个函数图像也可以用于表示 ![]() ,其横轴为
,其横轴为 ![]() ,纵轴为对应的常量
,纵轴为对应的常量 ![]() ,这便是
,这便是 ![]() 的标准频域图像,该函数也被称为频谱函数,正好是上面的第①个式子,其中横轴
的标准频域图像,该函数也被称为频谱函数,正好是上面的第①个式子,其中横轴 ![]() 对应着频率,而纵轴
对应着频率,而纵轴 ![]() 就对应着该频率的波的幅值
就对应着该频率的波的幅值
如果要更准确的说法,常量系数
应该是一个复数,因为不止考虑幅值,还应考虑相位,不过我觉得这篇文章作为科普性质的话,讲这个稍微有点超纲了,所以只需要尝试去理解下就好,后面就默认只考量幅值
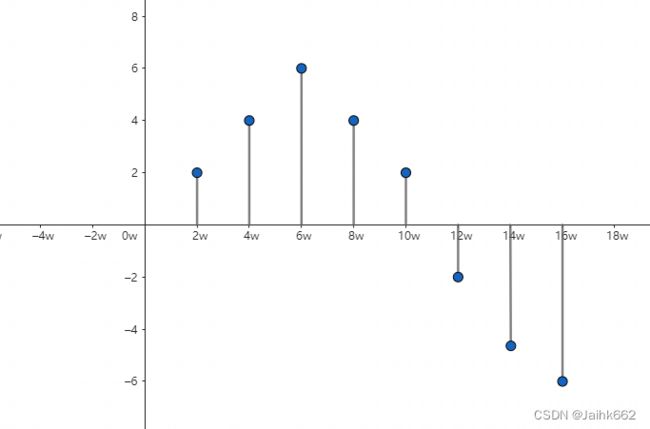
对于周期 T 有限的情况下,![]() 的结果是离散的,因此对于周期函数的频域图像,其更像是一个冲激函数图像,即只可能会在横轴坐标为
的结果是离散的,因此对于周期函数的频域图像,其更像是一个冲激函数图像,即只可能会在横轴坐标为 ![]() 的位置下出现非0的
的位置下出现非0的 ![]() 结果
结果
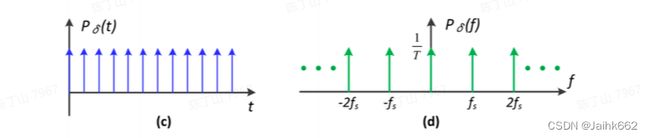
将频域图像和时域图像联系起来,就是下面这个样子(该图片来源于维基百科):
从频域图中也可以看出,周期函数 T 越大,对应的 w 越小,冲激函数的图像就越加密集,而对于非周期函数 T,其实也可以理解为 T 无穷大,此时对应的频率 w 无穷小,频域图像就看上去是连续的了:
同理,如果拉伸 ![]() 的时域图像,那么其频域图像则会被压扁
的时域图像,那么其频域图像则会被压扁
1.4.2 傅里叶变换的最终形式
基频 ![]() 相当于周期函数的傅里叶级数中两个相邻频率的差值
相当于周期函数的傅里叶级数中两个相邻频率的差值 ![]() ,当周期 T 无穷大时,我们可以把它记作
,当周期 T 无穷大时,我们可以把它记作 ![]() 或
或 ![]() ,这样就得到了针对非周期函数的频谱函数:
,这样就得到了针对非周期函数的频谱函数:
此时 ![]() 趋近于0,意义不大,但是我们可以将其带入到上面②式
趋近于0,意义不大,但是我们可以将其带入到上面②式  就有
就有
其中,傅里叶变换(FT) 即
如果文字和公式不好理解,那就上图:
对于 ![]() 的部分图像如上,那么该部分转成复数形式的
的部分图像如上,那么该部分转成复数形式的 ![]() 图像就为下(其中
图像就为下(其中 ![]() ,其取值越小,整体复平面下的图像就越“拥挤”,即这里的
,其取值越小,整体复平面下的图像就越“拥挤”,即这里的 ![]() 对应的是下图中的“转速”(0.2圈/秒),而非函数
对应的是下图中的“转速”(0.2圈/秒),而非函数 ![]() 的频率)
的频率)
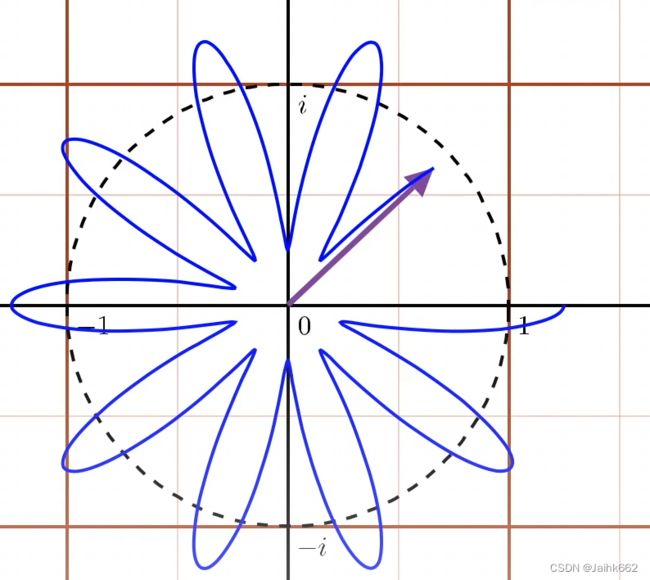
而很明显,我们最后对上面结果求得的积分,就是对这张图像无限延伸的版本中的无数个点对应的向量做加和,想象一下最终加和结果是什么样子的:
由于 ![]() ,只有时域周期满足
,只有时域周期满足 ![]() 的波形,最终得出的傅里叶变换结果不为0(左下图),并且会随着积分上下限的提高,得出的结果也越来越大,其余波形成的缠绕图像都会在复平面上均匀展开,从而得出0或者接近0的结果(右下图),从这也可以看出傅里叶变换滤波的特性
的波形,最终得出的傅里叶变换结果不为0(左下图),并且会随着积分上下限的提高,得出的结果也越来越大,其余波形成的缠绕图像都会在复平面上均匀展开,从而得出0或者接近0的结果(右下图),从这也可以看出傅里叶变换滤波的特性
好了,到此就完成了最前面右边那张 PPT 中的内容的推导,是不是还是挺简单的
当然也有可能看懂了推导过程,最后还是有疑问:折腾了这么久,傅立叶变换到底有什么意义和实际应用呢?不着急,到这里还只是一个开始,路还很长很长
1.4.3 一个形象的解释,为什么梳状函数的频域图像仍然是个梳状函数
以下图片同样节选自 Games101 中的第八章:光栅化(深度测试与抗锯齿)
左侧为梳状函数的时域图像
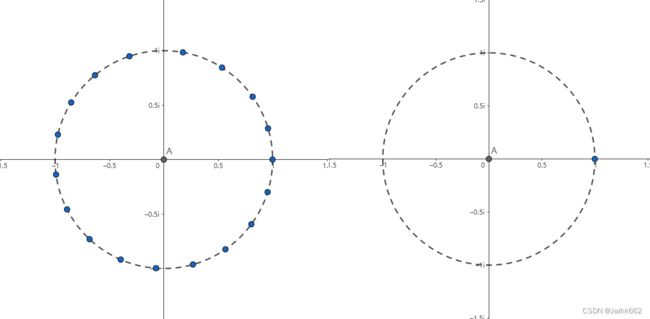
考虑到对于如上的冲激函数序列(即梳状函数)画出其指数空间下的图像
这个图像的性质就是:所有图像中的点都会遍布在单位圆上,并且脉冲信号越密或者采样时间越长,点在圆上的排列也越密,很好看出来:经过无穷时间后,所有的点就会汇集成一个标准的圆,此时做采样积分,最后得出的结果一定是无限接近于0的,但是只有一种情况特殊,那就是转速(s/circle)刚好和脉冲间隔 ![]() 完全一致或者说后者是前者的整数倍:此时所有的点都会落到图中的 (1, 0) 坐标上
完全一致或者说后者是前者的整数倍:此时所有的点都会落到图中的 (1, 0) 坐标上
因此,梳状函数的频域图像就也会是一段段脉冲信号的重复
其它参考:
- 快速理解FFT算法(完整无废话)
- 一小时学会快速傅里叶变换
- 【官方双语】形象展示傅里叶变换
-
快速傅里叶变换(FFT)超详解