离散傅立叶变换在图像处理中的推导和意义

傅立叶变换(FT)能应用的领域太多了，本文聊聊FT在图像处理上的应用。前有高人不用公式通俗地解释了傅立叶级数，傅立叶变换等概念(傅立叶变换讲解－知乎专栏, 任意取的一个名字，还望作者不要在意)。 本文目的是更深入地理解一下傅立叶变换在图像处理领域的应用，包括如何推导公式和变换后频谱图的物理意义。

为了表述方便，是会用到公式的，但是对数学方面的要求就是会解多元一次方程组就行。

1. 傅立叶变换的基础知识

根据傅立叶级数的知识，对于任意一个周期为的函数，它可以被表示成一系列正弦波和余弦波的叠加：

其中。

相信看过Heinrich大神那篇文章对这个就很容易理解，Wiki的图再放一遍 傅立叶级数动图。

非周期函数没有傅立叶级数，但是我们可以把它看成一个无限大的周期函数。此时，趋向于0，用积分的思想仍然可以把任意函数表示成正弦波和余弦波的叠加。

以上就是傅立叶变换的核心思想，任何信号都可以表示成一系列正弦波和余弦波的和的形式。不再赘述。

 

2. 图片傅立叶变换公式的推导

这一部分主要阐述如何在图片数据上进行傅立叶变换。

通用傅立叶公式是：

意思就是现实中的一个任意数据，是由很多频率的正弦，余弦波叠加组成。其中是频率为的正弦波幅度与余弦波幅度计算出的一个数值，是t从到时，的积分。这个公式不太好理解，比如为什么是负无穷到正无穷？为什么会出现自然对数？为什么会有虚数？不是说有正余弦波吗，在哪里呢？好混乱啊，这是因为理解一个东西就像是在爬楼梯，一阶一阶地上，任何人都可以毫不费力地走上去。但是如果楼梯缺了几块，就会觉得走上去很难。直接看这个公式就是让人直接从地面跳到十层楼的楼顶，对任何人都难。因为傅立叶变换的推导过程比较繁杂，最后看到的公式推想物理意义很难。我们想的是，从基本思想推导出公式。

 

一个灰度图片是以一个二维矩阵的形式存在，和通用傅立叶变换相比，有俩点不同：

• 图片是二维，公式是一维

• 图片数据有限且离散，公式无限且连续。

有很多资料在说在图片傅立叶变换中，一个图片会被分成8*8的小块，再进行计算。这可能是在实现时候提高运算效率的一种方法，但是我觉得这对理解傅立叶变换物理意义造成了影响。我们按照公式去实现了一下，先不考虑运算效率问题，也就是说不把图片分成小块，代码在这里： DFT 简单实现－Matlab。

• 二维的问题

二维矩阵中每一列（或者每一行）数据都可以单独看作一个波。对一个的矩阵，可以看作个的波。在二维傅立叶变换里，先分别对每一列（行）做傅立叶变换，会得到同样大小的傅立叶系数向量，再在另一个维度（上面是行这里就是列，上面是列这里就是行）对这些系数做傅立叶变换。所以，研究二维傅立叶变换可以看成俩个一维傅立叶变换，本质上还是一维数据的处理。

 

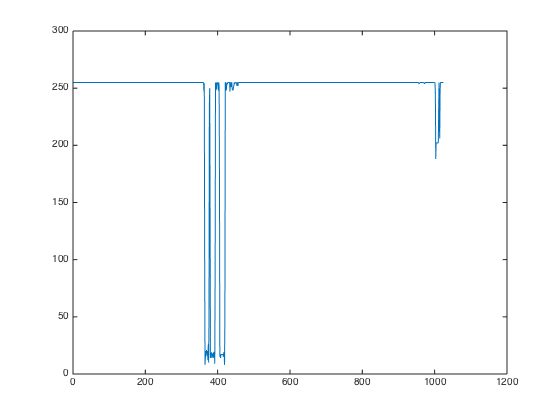
从第三部分“频谱图的理解”插图的左上角原图里，我们拿出第100列的数据，是一个个像素的值，以1-1024之间的整数做X轴，以像素的值做Y轴，画出这个向量的波是：

 

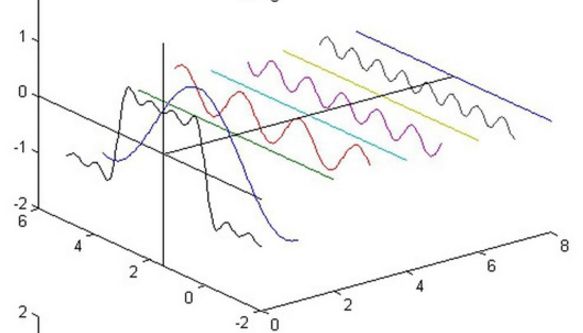
这个波和我们在所有地方看到的信号是一样的，可以看成是多个正余弦波的叠加。盗图一张，同样出自傅立叶变换讲解－知乎专栏，写的真好：

最左侧那个波可以看作图片中一行或者一列的数值组成的波，后面是分解出来的不同幅度，不同频率的正弦和余弦波。

• 关于无限到有限的问题

 

在实际情况中，无穷大是没有办法实现的，只能近似估计。图片的一维数据是一个波，我们假设这个波由P个频率的波叠加而成。

 

图片中的像素值是：

－星标公式 (后文用“星标公式”来引用它)

其中是所有频率波中的单位频率，它决定了波叠加的效果，后面谈。

如果可以求出和的值，就完成了离散傅立叶变换。 也就是时域到频域的转换：因为我们求出了组成图像数据的各个频率的波及其幅度。

 

到目前为止，所有的概念都很直观：图像中一列数据组成的波，可以看作是个频率的正弦和余弦波叠加而成，这些波具有不同的振幅，我们的目的就是求出这些振幅的具体数值。对于一列图像的像素值，如果它的大小是，也就是说有个的值，而未知数共有个。根据解方程的思想，可以代入每一个像素的值，解出各个和的值。但是，还有一个问题：单位频率还是未知的。

那么是不是随意给一个值就可以呢？当然不是的，需要明白频率对于一组数据的作用。决定了这组数据的伸缩程度。看一种特殊情况，在星标公式中，令, , , , 随意取俩个频率, , 我们得到俩组数据：

和

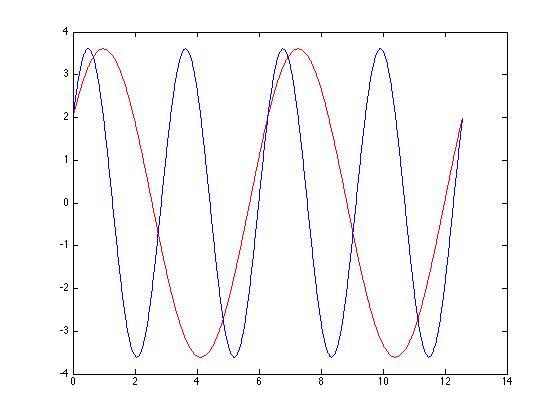
让，画出这俩组数据分别为(红色对应，蓝色对应)：

 

可以看到，上图中蓝色形状有4个周期，红色形状有2个周期，蓝色波相当于是红色波在横轴上的缩放。所以单位频率主要决定的是数组的缩放程度，数据的重复周期是。真实图片的波形太难画了，随意一张图片的一列数据都是几十几百个的正余弦波形，但是道理是一样的，单位频率取值不同时，所有波形综合而成的数据相应的伸缩变化。

在一个图片中，取出其中一列数据( 的向量)做傅立叶变换，把取出的这列数据看作是周期为的周期数据最容易解决问题。想象一下，在一张图片的上下俩侧平铺无数张同样的图片，那我们取出的这一列数据不就变成一个的周期函数中的一段了么。此时取单位频率 。

• 傅立叶变换复数形式

我们确定了图像上的一列像素是由个频率的波叠加而成的，这些波的单位频率，其实就可以算出所有想要的所有东西了，也可以说，星标公式才是傅立叶变换在图像处理中应用的真身。为什么我们查到的都是带虚数，带的那个复杂的公式？这是为了表述起来方便，把 和 综合成一项，把星标公式改写的一种形式。根据欧拉公式，余弦和正弦函数可以表示为：

和

 

所以信号就可以表示为：

当时，使

，

,

，

由于单位频率，有一个这样的特殊条件：。所以，信号又可以表示为一种复数形式：

，其中

在上式中，一列的图像数据提供个，而右式有个未知数，很神奇，太契合了啊，太神奇了。

 

计算过程

 

傅立叶变换的算法就是在计算的值。

当时:

当时:

当时:

...

当时:

之后就是简单的解方程了。

使

c_m和图像像素值之间的关系是：

而参数的值即是：

由于的特殊情况，以及正余弦函数的特性，

 

所以，图片一维傅立叶变换的公式是：

,

不过查到的资料好像都把前面的 省略掉了，这样计算出的值就是实际的倍。这就是具体的计算方法的问题了，原理上乘以一个常数不影响，逆变换需要实际的像素值，是需要乘以的。

二维的公式就是：

 

3. 频谱图的理解

在我搜索资料的过程中，发现了很多问题是关于频谱图代表什么物理意义的。其实理解了上一部分，这个物理意义也很容易了。频谱图里每一个像素上的值就是的值。

上一部分的公式中计算出的 并没有什么物理意义，组成它的和才有。但是 ，所以可以用来代表这个频率波的振幅大小。

下图中是某个图片做了DFT之后前5行和前5列的值，的值是相应的：

 

从上图也可以看得出，DFT之后的数值非常大，以图片形式显示不出，强行显示就是下图右上角的样子。所以会把映射到一个可显示的空间，比如。对一幅图片：

 

在各类资料里，我们看到的频谱图都是右下角那样。把映射到可显示空间之后可以看到，数值应该像左下角的图一样。前文已经说过，对一个的信号，其由个频率的波叠加，计算所得数据左右上下对称，因为当时，和共轭存在。对一个的图片的某个像素，经过它的俩个频率分别是，。所以，越是靠近角落的地方就越是低频的波。

在这个频谱图上，值有大有小，每一个点都是用来计算不同频率波的振幅幅度。一定程度上，每个点的值也可以反映某个频率的波的振幅。很容易观察到，四个角落上的值会亮一些，说明低频的波振幅大一些。所以为了便于观察，互换角落和图片中心位置的数值，就得到右下角的图。频谱图和原图并没有什么对应关系，频谱图上每一个点都是第二部分中所述的c_m的值，代表了一个频率的正弦波的幅度和余弦波的幅度乘以虚数i相加的结果，具体什么物理意义，也谈不上吧。

之前看过一些说法是FT可以使能量集中，因为低频的振幅更大一些。但是这个并不是因为傅立叶变换有使数据可以集中到某一块的特性，而是自然界中存在的各种信号(图片和声音)本来就大多集中在低频。 图片信息中，人眼对低频的感知更敏感，对高频信息不敏感。

 

4. 傅立叶变换在图像处理中的应用

理解了以下俩点：

• 图片是波，这个波可以看成N个正弦，余弦波的叠加

• 大自然中的各种信号的大部分信息都集中在低频，而且人眼对低频更敏感

就很容易明白傅立叶变换在图像处理中的应用。

在去噪上的原理和缺陷： 当图像出现的噪声是有规律的，相当于让某个频率波的幅度增大，把这个值减小，就是去掉这个频率的波，所以可以去噪，比如高斯噪声。当出现的噪声是没有规律的，随机出现的一些东西，FT是没有作用的。

在图片压缩方面，根据傅立叶变换推导出的DCT有很重要作用。JPEG格式的图片就是用Huffman编码方式压缩图片的DCT的系数。

当然，FT还是通信行业的基础，傅立叶变换在打电话这个过程有重要作用，声音信号的调制和解调。

 

From: https://zhuanlan.zhihu.com/p/23607336