神经网络与深度学习作业10:(LSTM | GRU)
神经网络与深度学习作业10:(LSTM | GRU)
- 习题6-3当使用公式(6.50)作为循环神经网络的状态更新公式时,分析其可能存在梯度爆炸的原因并给出解决方法.
- 习题6-4推导LSTM 网络中参数的梯度,并分析其避免梯度消失的效果.
- 习题6-5推导GRU网络中参数的梯度,并分析其避免梯度消失的效果. (选做)
- 附加题6-1P:什么时候应该用GRU?什么时候用LSTM?(选做)
- 附加题6-2P: LSTM BP推导,并用Numpy实现.(选做)
- 总结
- References:
习题6-3当使用公式(6.50)作为循环神经网络的状态更新公式时,分析其可能存在梯度爆炸的原因并给出解决方法.
梯度爆炸问题:在公式 Z k = U h k − 1 + W x k + b Z_k=Uh_{k-1}+Wx_k +b Zk=Uhk−1+Wxk+b 为在第 k k k时刻函数 g ( ∗ ) g(*) g(∗)的输入,在计算公式(6.34)中的误差项 δ t , k = ∂ L t ∂ z k δ_{t,k} = \frac{\partial L_{t}}{\partial z_{k}} δt,k=∂zk∂Lt,梯度可能会过大,从而导致梯度爆炸问题。
解决办法:增加门控装置。
习题6-4推导LSTM 网络中参数的梯度,并分析其避免梯度消失的效果.
f t = σ ( W f ∗ ( h t − 1 , x t ) + b f ) f_t = σ(W_f*(h_{t-1},x_t) + b_f) ft=σ(Wf∗(ht−1,xt)+bf)
i t = σ ( W i ∗ ( h t − 1 , x t ) + b i ) i_t = σ(W_i*(h_{t-1},x_t) + b_i) it=σ(Wi∗(ht−1,xt)+bi)
C t ~ = t a n h ( W c ∗ ( h t − 1 , x t ) + b c ) \tilde{C_t} = tanh(W_c*(h_{t-1},x_t) + b_c) Ct~=tanh(Wc∗(ht−1,xt)+bc)
C t = f t ∗ C t − 1 + i t ∗ C t ~ C_t = f_t*C_{t-1} + i_t*\tilde{C_t} Ct=ft∗Ct−1+it∗Ct~
O t = σ ( W o ∗ ( h t − 1 , x t ) + b o ) O_t = σ(W_o*(h_{t-1},x_t) + b_o) Ot=σ(Wo∗(ht−1,xt)+bo)
h t = O t ∗ t a n h ( C t ) h_t = O_t*tanh(C_t) ht=Ot∗tanh(Ct)
∂ E k ∂ W = ∂ E k ∂ h k ∗ ∂ h k ∂ C k ∗ . . . ∗ ∂ C 2 ∂ C 1 ∗ ∂ C 1 ∂ W = ∂ E k ∂ h k ∗ ∂ h k ∂ C k ( ∏ t = 2 k ∂ C t ∂ C t − 1 ) ∗ ∂ C 1 ∂ W \frac{\partial E_{k}}{\partial W} = \frac{\partial E_{k}}{\partial h_k}*\frac{\partial h_{k}}{\partial C_k}*...*\frac{\partial C_{2}}{\partial C_1}*\frac{\partial C_{1}}{\partial W} = \frac{\partial E_{k}}{\partial h_k}*\frac{\partial h_{k}}{\partial C_k}(\prod_{t=2}^{k}\frac{\partial C_{t}}{\partial C_{t-1}})*\frac{\partial C_{1}}{\partial W} ∂W∂Ek=∂hk∂Ek∗∂Ck∂hk∗...∗∂C1∂C2∗∂W∂C1=∂hk∂Ek∗∂Ck∂hk(∏t=2k∂Ct−1∂Ct)∗∂W∂C1
展开得到:
C t = C t − 1 ∗ σ ( W f ∗ ( h t − 1 , x t ) + b f ) + t a n h ( W c ∗ ( h t − 1 , x t ) ) ∗ σ ( W i ∗ ( h t − 1 , x t ) ) C_t = C_{t-1}*σ(W_f*(h_{t-1},x_t) + b_f)+tanh(W_c*(h_{t-1},x_t))*σ(W_i*(h_{t-1},x_t)) Ct=Ct−1∗σ(Wf∗(ht−1,xt)+bf)+tanh(Wc∗(ht−1,xt))∗σ(Wi∗(ht−1,xt))
求导得:
∂ C t ∂ C t − 1 = ∂ f t ∂ C t − 1 ∗ C t − 1 + ∂ C t − 1 ∂ C t − 1 ∗ f t + ∂ i t ∂ C t − 1 ∗ C t ~ ∗ i t = σ ′ ( W f ∗ ( h t − 1 , x t ) ) W f ∗ O t − 1 ⊗ t a n h ′ ( C t − 1 ) ∗ C t − 1 + f t + σ ′ ( W i ∗ ( h t − 1 , x t ) ) W i ∗ O t − 1 ⊗ t a n h ′ ( C t − 1 ) ∗ C t ~ + σ ′ ( W c ∗ ( h t − 1 , x t ) ) W c ∗ O t − 1 ⊗ t a n h ′ ( C t − 1 ) ∗ i t \frac{\partial C_{t}}{\partial C_{t-1}}=\frac{\partial f_{t}}{\partial C_{t-1}}*C_{t-1}+\frac{\partial C_{t-1}}{\partial C_{t-1}}*f_{t}+\frac{\partial i_{t}}{\partial C_{t-1}}*\tilde{C_t}*i_t = σ^{'}(W_f*(h_{t-1},x_t))W_f*O_{t-1}\otimes tanh^{'}(C_{t-1})*C_{t-1} + f_t+σ^{'}(W_i*(h_{t-1},x_t))W_i*O_{t-1}\otimes tanh^{'}(C_{t-1})*\tilde{C_t} +σ^{'}(W_c*(h_{t-1},x_t))W_c*O_{t-1}\otimes tanh^{'}(C_{t-1})*i_t ∂Ct−1∂Ct=∂Ct−1∂ft∗Ct−1+∂Ct−1∂Ct−1∗ft+∂Ct−1∂it∗Ct~∗it=σ′(Wf∗(ht−1,xt))Wf∗Ot−1⊗tanh′(Ct−1)∗Ct−1+ft+σ′(Wi∗(ht−1,xt))Wi∗Ot−1⊗tanh′(Ct−1)∗Ct~+σ′(Wc∗(ht−1,xt))Wc∗Ot−1⊗tanh′(Ct−1)∗it
其中 E E E为损失函数,由于LSTM中通过门控机制解决梯度问题,遗忘门,输入门和输出门是非0就是1的,并且三者之间都是相加关系,梯度能够很好的在LSTM传递,减轻了梯度消失发生的概率,门为0时,上一刻的信息对当前时刻无影响,没必要接受传递更新参数了。
习题6-5推导GRU网络中参数的梯度,并分析其避免梯度消失的效果. (选做)
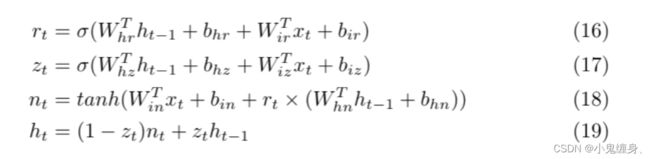
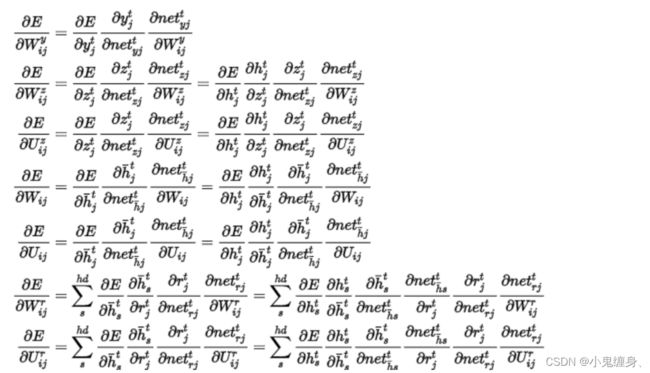
则有:
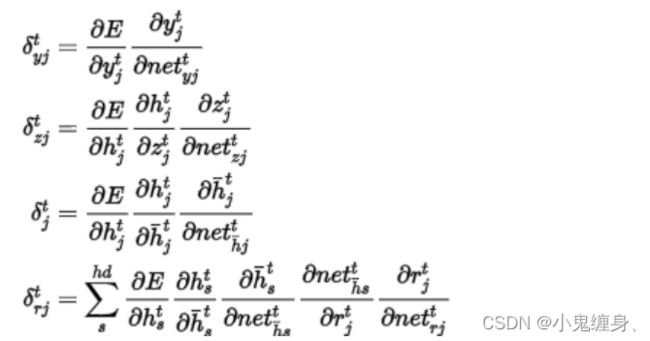
即:
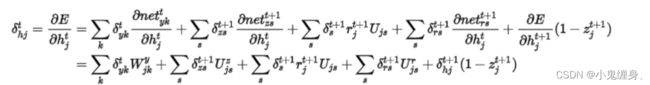
表示:
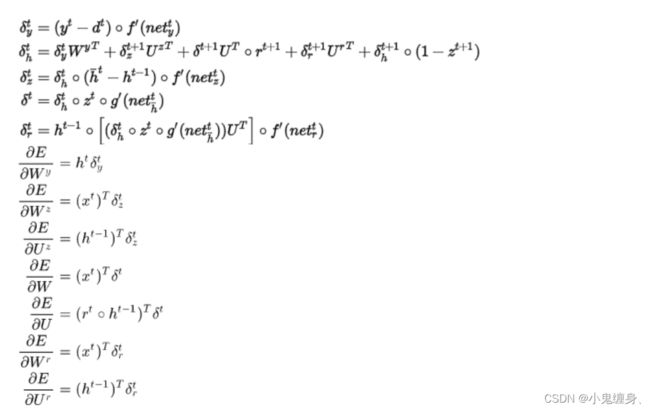
分析:
GRU具有调节信息流动的门单元,但没有一个单独的记忆单元,GRU将输入门和遗忘门整合成一个升级门,通过门来控制梯度。这种门控的方式,让网络学会如何设置门控数值,来决定何时让梯度消失,何时保持梯度。
附加题6-1P:什么时候应该用GRU?什么时候用LSTM?(选做)
先说一下两者的区别:
GRU通过更新门来控制上一时刻的信息传递和当前时刻计算的隐层信息传递。GRU中由于是一个参数进行控制,因而可以选择完全记住上一时刻而不需要当前计算的隐层值,或者完全选择当前计算的隐层值而忽略上一时刻的所有信息,最后一种情况就是无论是上一时刻的信息还是当前计算的隐层值都选择传递到当前时刻隐层值,只是选择的比重不同。
而LSTM是由两个参数(遗忘门和输入门)来控制更新的,他们之间并不想GRU中一样只是由一个参数控制,因而在比重选择方面跟GRU有着很大的区别,例如它可以既不选择上一时刻的信息,也不选择当前计算的隐层值信息(输入门拒绝输入,遗忘门选择遗忘)。
GRU要在上一时刻的隐层信息的基础上乘上一个重置门,而LSTM无需门来对其控制。
LSTM必须考虑上一时刻的隐层信息对当前隐层的影响,而GRU则可选择是否考虑上一时刻的隐层信息对当前时刻的影响。
总结:可以看出的是,GRU结构相比与LSTM模型结构简单,适用于构建较大的网络,计算的效率也比LSTM更高。但是对于结果和准确性而言,LSTM更具灵活性和强大。
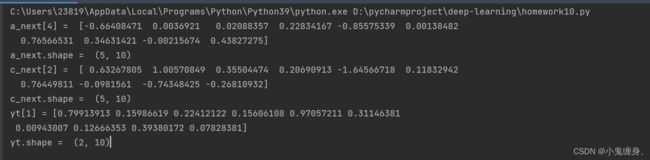
附加题6-2P: LSTM BP推导,并用Numpy实现.(选做)
numpy实现代码:
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
e_x = np.exp(x-np.max(x))# 防溢出
return e_x/e_x.sum(axis=0)
def LSTM_CELL_Forward(xt, h_prev, C_prev, parameters):
"""
Arguments:
xt:时间步“t”处输入的数据 shape(n_x,m)
h_prev:时间步“t-1”的隐藏状态 shape(n_h,m)
C_prev:时间步“t-1”的memory状态 shape(n_h,m)
parameters
Wf 遗忘门的权重矩阵 shape(n_h,n_h+n_x)
bf 遗忘门的偏置 shape(n_h,1)
Wi 输入门的权重矩阵 shape(n_h,n_h+n_x)
bi 输入门的偏置 shape(n_h,1)
Wc 第一个“tanh”的权重矩阵 shape(n_h,n_h+n_x)
bc 第一个“tanh”的偏差 shape(n_h,1)
Wo 输出门的权重矩阵 shape(n_h,n_h+n_x)
bo 输出门的偏置 shape(n_h,1)
Wy 将隐藏状态与输出关联的权重矩阵 shape(n_y,n_h)
by 隐藏状态与输出相关的偏置 shape(n_y,1)
Returns:
h_next -- 下一个隐藏状态 shape(n_h,m)
c_next -- 下一个memory状态 shape(n_h,m)
yt_pred -- 时间步长“t”的预测 shape(n_y,m)
"""
# 获取参数字典中各个参数
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 获取 xt 和 Wy 的维度参数
n_x, m = xt.shape
n_y, n_h = Wy.shape
# 拼接 h_prev 和 xt
concat = np.zeros((n_x + n_h, m))
concat[: n_h, :] = h_prev
concat[n_h:, :] = xt
# 计算遗忘门、输入门、记忆细胞候选值、下一时间步的记忆细胞、输出门和下一时间步的隐状态值
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * C_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
h_next = ot * np.tanh(c_next)
# LSTM单元的计算预测
yt_pred = softmax(np.dot(Wy, h_next) + by)
return h_next, c_next, yt_pred
np.random.seed(1)
xt = np.random.randn(3,10)
h_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
h_next, c_next, yt = LSTM_CELL_Forward(xt, h_prev, c_prev, parameters)
print("a_next[4] = ", h_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
总结
这次作业感觉还是收获很多的,看了很多大佬的博客,都写的很详细,确实感觉到自己的差距很大,还是要好好努力的。
References:
【手撕LSTM】LSTM的numpy实现
人人都能看懂的LSTM介绍及反向传播算法推导(非常详细)
GRU和LSTM在各种使用场景应该如何选择?
GRU是什么?RNN、LSTM分别是什么?
GRU和LSTM区别
GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现
神经网络中梯度的概念,神经网络梯度公式推导
彻底看懂RNN,LSTM,GRU,用数学原理解释梯度消失或者梯度爆炸
LSTM,GRU为什么可以缓解梯度消失问题?
老师的博客:
NNDL 作业10:第六章课后题(LSTM | GRU)