PCL-3D特征描述子

3D特征描述子

• 什么是3D特征描述子？
• 特征描述子 Feature Descriptor
  • 是每个特征点独特的身份认证
  • 同一空间点在不同视角的特征点具有高度相似的描述子
  • 不同特征点的描述子差异性尽量大
  • 通常描述子是一个具有固定长度的向量

描述子可以分为以下几种类型：基于不变性的描述子、基于直方图的描述子、二进制描述子
PCL主要实现了：

1. NARF特征点描述子
2. PFH(FPFH)点特征直方图描述子
3. RoPs 特征
4. VFH视点特征直方图描述子
5. GASD全局对齐的空间分布描述子
6. 基于惯性矩和偏心率的描述子

PFH点特征直方图描述子

表面法线和曲率估计是某个点周围的几何特征的基本表示方法。虽然计算起来比较容易，但是能够提供的信息并不多。因为他们只是用很少的几个参数值近似地表示一个点的k邻域几何特征。大部分场景下都会有很多相同或相似的特征值，故而只采用点特征就会少了很多全局的特征信息。
我们可以通过点特征直方图（Point Feature Histograms， PFH）来采集详细的特征信息。

基础理论

• PFH方法流程如下，先看下图：

• 我们首先确定一个k的数值(或者半径)，对范围内的目标点p以及目标点的k临近点，做两两组合。我们需要通过一种手段来描述这些点对之间的法线$n$和位置的相对信息。

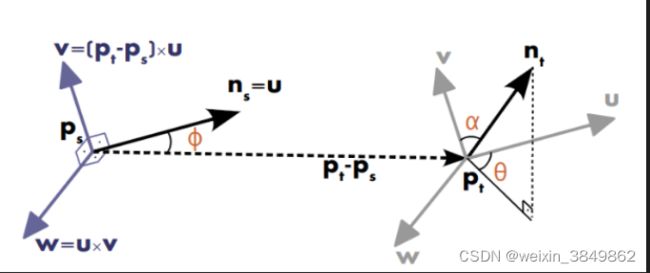
• 首先设定两个k临近范围内的点，$p_s$和$p_t$,以及它们对应的法线$n_s$和$n_t$. 我们先看下面的图以$p_s$作为初始坐标点

---

---

---

这里d表示$P_t,P_s$之间的欧式距离，即$d=||P_t-P_s|{|}^2$,通过计算每一个点对的$<\alpha ,\varphi ,\theta ,d>$,就可以把两个点之间法向量的12(2x旋转自由度x平移自由度)个参数变成4个。
以下代码为每个点估算PFH四元组，可以使用以下代码：

#include 
/** \brief 计算点对的PFH特征的4个特征元素值，包含3个角度值和一个两点间的距离值
  * \param[in] p1 the first XYZ point 第一个点的xyz坐标
  * \param[in] n1 the first surface normal 第一个点所在区域的表面法向量
  * \param[in] p2 the second XYZ point 第二个点的xyz坐标
  * \param[in] n2 the second surface normal 第二个点所在区域的表面法向量
* \param[out] f1 第一个角度特征值 Θ (angle between the projection of nq_idx and u)
* \param[out] f2 第二个角度特征值 α (angle between nq_idx and v)
* \param[out] f3 第三个角度特征值 Φ (angle between np_idx and |p_idx - q_idx|)
* \param[out] f4 两点间的欧式距离 d (p_idx - q_idx)
*/

computePairFeatures (const Eigen::Vector4f &p1, const Eigen::Vector4f &n1, 
                     const Eigen::Vector4f &p2, const Eigen::Vector4f &n2, 
                     float &f1, float &f2, float &f3, float &f4);

下面是PFH直方图的统计方式

1. 将<α,ϕ,θ,d>中的每个特征值范围划分为b个子区间（默认为5，这个数值可以自行计算并设置），则4个特征共有$b^4$个子区间。我们设b=5,那么子空间的数量就是625个子空间，但是往往d不计入其中，因此仅125个子空间。
2. 现在我们的直方图就是625维度(125维度，如果是三个特征向量)，看看对应的特征值（如[1,1,1,1]）落入那个子空间中，最后统计k临近范围内所有点对，落入的不同子空间的数量，就可以变成直方图了。
3. 由于<α,ϕ,θ>三个特征都是法线之间的角度信息，则它们的值很可能会归为同一个空间(范围内）。

注意：在一些情况下，第四个特征d通常跟设备捕获2.5D深度数据是相关的，临近点的距离d是从视点开始递增的，在不同视角下，这些值的变化意义不大，所以在扫描局部点密度影响特征时，省略距离d效果会更好。

---

默认PFH的实现，对每个特征都使用5个子区间进行分类，这里不包括距离d。这样就组成了一个125个浮点数元素的特征向量（53），保存在数据类型pcl::PFHSignature125中。

/** \brief Estimate the PFH (Point Feature Histograms) individual signatures of the three angular (f1, f2, f3)
* features for a given point based on its spatial neighborhood of 3D points with normals
* \param[in] cloud the dataset containing the XYZ Cartesian coordinates of the two points
* \param[in] normals the dataset containing the surface normals at each point in \a cloud
* \param[in] indices the k-neighborhood point indices in the dataset
* \param[in] nr_split the number of subdivisions for each angular feature interval
* \param[out] pfh_histogram the resultant (combinatorial) PFH histogram representing the feature at the query point
*/
void 
computePointPFHSignature (const pcl::PointCloud &cloud,
                          const pcl::PointCloud &normals, 
                          const std::vector &indices, int nr_split,
                          Eigen::VectorXf &pfh_histogram);

参数说明：

1. cloud：包含xyz坐标点信息的数据集
2. normals：数据集中点的法向量信息
3. indices：指定查询点，数据集中k邻域点的索引
4. nr_split：每个角特征的区间数,默认为5
5. pfh_histogram（输出）：结果PFH直方图，表示查询点处的特征

#include 
#include 

#include 
#include 
#include 
#include 

int main()
{
    // load point cloud
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
    //    pcl::io::loadPCDFile("./data/target.pcd", *cloud);
    pcl::io::loadPCDFile("./data/bunny.pcd", *cloud);

    // estimate normals ------------------------------------------------------------- 计算法向量
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    // Object for normal estimation.
    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
    //normalEstimation.setIndices()
    normalEstimation.setInputCloud(cloud);

    // For every point, use all neighbors in a radius of 3cm.
    normalEstimation.setRadiusSearch(0.03);

    // A kd-tree is a data structure that makes searches efficient. More about it later.
    // The normal estimation object will use it to find nearest neighbors.
    pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
    normalEstimation.setSearchMethod(kdtree);
    // Calculate the normals.
    normalEstimation.compute(*normals);

    // Create the PFH estimation class, and pass the input dataset+normals to it ------计算PFH直方图
    pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;
    pfh.setInputCloud(cloud);
    pfh.setInputNormals(normals);

    // alternatively, if cloud is of tpe PointNormal, do pfh.setInputNormals (cloud);
    // Create an empty kdtree representation, and pass it to the PFH estimation object.
    // Its content will be filled inside the object, based on the given input dataset (as no other search surface is given).
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());
    //pcl::KdTreeFLANN::Ptr tree (new pcl::KdTreeFLANN ()); -- older call for PCL 1.5-
    pfh.setSearchMethod(tree);

    // Output datasets
    pcl::PointCloud<pcl::PFHSignature125>::Ptr pfhs(new pcl::PointCloud<pcl::PFHSignature125>());
    // Use all neighbors in a sphere of radius 5cm
    // 使用一个半径为5厘米的球体，作为搜索邻域
    // IMPORTANT: the radius used here has to be larger than the radius used to estimate the surface normals!!!
    // 重点： 半径必须要比用于估算法向量的邻域半径要大

    pfh.setRadiusSearch(0.08);

    // Compute the features
    pfh.compute(*pfhs);

    unsigned long size = pfhs->points.size();
    for (int j = 0; j < size; ++j) {
        pcl::PFHSignature125 &signature125 = pfhs->points[j];
        float* h = signature125.histogram;

        printf("%d: %f,%f,%f \n", j, h[1], h[2], h[3]);
    }

    // visualize normals
    pcl::visualization::PCLVisualizer viewer("PCL Viewer");
    viewer.setBackgroundColor(0.0, 0.0, 0.5);
    viewer.addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals, 1, 0.01, "normals");

    while (!viewer.wasStopped()) {
        viewer.spinOnce();
    }
    return 0;
}

FPFH快速点特征直方图描述子

如果点云P中有n个点，则其点特征直方图PFH的理论计算复杂度$O(n{k}^2)$，其中k是点云P中每个点p计算特征向量时，要考虑的邻域数量。对于实时应用或近实时应用，密集点云的点特征直方图PFH的计算，是一个主要的性能瓶颈，故而我们可以将之进行简化，称为快速点特征直方图FPFH（Fast Point Feature Histograms）。这个FPFH将计算复杂度降到了O(nk)，但是仍然保留了PFH大部分的识别特性。

FPFH计算过程

1. 为查询点求得它和其k邻域内每个点之间的三个特征元素值(不算d)，然后统计成一个SimplePFH；
2. 分别对k邻域中的每个点确定k邻域，按第一步分别形成自己的SPFH；
3. 对邻域中的各个SPFH进行加权统计，得到最终的FPFH公式如下：
   

---

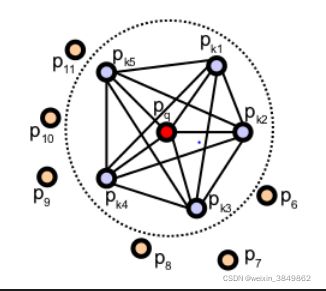
FPFH快点特征直方图的影响区域图。 每个查询点（红色）仅连接到其直接的k邻居（由灰色圆圈包围）。 每个直接邻居都连接到其自己的邻居，并将所得直方图与查询点的直方图一起加权以形成FPFH。 较粗的连接两次会被重复计数2次（比较重要的点对）。(这里很难理解，为什么计算复杂度会被降到K，如果重复的点对，会被重复计数，但不需要重新计算到确实有可能) (现在理解了，重复的点对会被重复计数，但不需要被重新计算)

FPFH与PFH的主要区别

1. FPFH没有对全互连点的所有邻近点的计算参数进行统计，因此可能漏掉了一些重要的点对，而这些漏掉的对点可能对捕获查询点周围的几何特征有贡献；
2. PFH特征模型是对查询点周围的一个精确的邻域半径内，而FPFH还包括半径r范围以外的额外点对（但不超过2r的范围）；
3. 因为采用权重计算的方式，所以FPFH结合SPFH值，重新捕获邻近重要点对的几何信息；
4. 由于FPFH大大地降低了PFH的整体复杂性，因此FPFH经常使用在实时应用中；
5. 通过分解三元组，简化了合成的直方图。也就是简单生成d分离特征直方图，对每个特征维度来单独绘制，并把它们连接在一起。（这里我来解释一波吧，比如PFH三个特征对应于125个子空间，也就是5x5x5，这是空间耦合的结果，如[1,1,1]落在1号空间里面，统计结果+1.但在FPFH里面应该5+5+5=15，这种情况下[1,1,1]再三个特征段里面各加一个1，也就是统计结果+3.

默认pcl实现的的FPFH使用11个统计区间（对每个特征值都将其参数区间分割为11个），分别计算特征直方图，然后合并得到了一个33个元素的特征向量，保存在数据类型pcl::FPFHSignature33中。

代码实现

#include 
#include 

#include 
#include 
#include 
#include 

int main()
{
    // load point cloud
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
    //    pcl::io::loadPCDFile("./data/target.pcd", *cloud);
    pcl::io::loadPCDFile("./data/bunny.pcd", *cloud);

    // estimate normals ------------------------------------------------------------- 计算法向量
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    // Object for normal estimation.
    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
    //normalEstimation.setIndices()
    normalEstimation.setInputCloud(cloud);

    // For every point, use all neighbors in a radius of 3cm.
    normalEstimation.setRadiusSearch(0.03);

    // A kd-tree is a data structure that makes searches efficient. More about it later.
    // The normal estimation object will use it to find nearest neighbors.
    pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
    normalEstimation.setSearchMethod(kdtree);
    // Calculate the normals.
    normalEstimation.compute(*normals);

    // Create the FPFH estimation class, and pass the input dataset+normals to it
    pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;
    fpfh.setInputCloud (cloud);
    fpfh.setInputNormals (normals);
    
    // alternatively, if cloud is of tpe PointNormal, do fpfh.setInputNormals (cloud);
    // Create an empty kdtree representation, and pass it to the FPFH estimation object.
    // Its content will be filled inside the object, based on the given input dataset (as no other search surface is given).
    pcl::search::KdTree<PointXYZ>::Ptr tree (new pcl::search::KdTree<PointXYZ>);
    fpfh.setSearchMethod (tree);
    // Output datasets
   pcl::PointCloud<pcl::FPFHSignature33>::Ptr fpfhs (new pcl::PointCloud<pcl::FPFHSignature33> ());

   // Use all neighbors in a sphere of radius 5cm
   // IMPORTANT: the radius used here has to be larger than the radius used to estimate the surface normals!!!
    fpfh.setRadiusSearch (0.05);
 
    // Compute the features
    fpfh.compute (*fpfhs);

    unsigned long size = fpfhs->points.size();
    for (int j = 0; j < size; ++j) {
        pcl::FPFHSignature33 &signature33 = fpfhs->points[j];
        float* h =signature33.histogram;

        printf("%d: %f,%f,%f \n", j, h[1], h[2], h[3]);
    }

    // visualize normals
    pcl::visualization::PCLVisualizer viewer("PCL Viewer");
    viewer.setBackgroundColor(0.0, 0.0, 0.5);
    viewer.addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals, 1, 0.01, "normals");

    while (!viewer.wasStopped()) {
        viewer.spinOnce();
    }
    return 0;
}

利用OpenMP提高FPFH的计算速度

对于计算速度要求苛刻的用户，PCL提供了一个FPFH估计的另一实现，它使用多核/多线程规范，利用OpenMP开发模式来提高计算速度。这个类的名称是pcl::FPFHEstimationOMP，并且它的应用程序接口（API）100%兼容单线程pcl::FPFHEstimation，这使它适合作为一个替换元件。在8核系统中，OpenMP的实现可以在6-8倍更快的计算时间内完全同样单核系统上的计算。

VFH视点特征直方图描述子

源于FPFH描述子，为了使构造的特征保持缩放不变性的同时，还要区分不同的位姿，因而计算时，需要加入视点信息。VFH时点特征直方图包含两个部分：

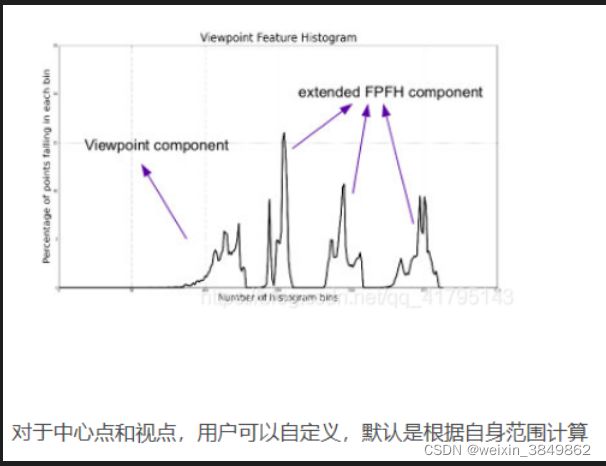
1. 视点方向的相关分量
2. 包含扩展FPFH的描述表面形状的分量
   这个理解相对简单一点
3. 视点与其他点的关系
4. 中心点与其他点的关系
   视点与其他点的关系：视点与中心点形成的向量与其他点法向量形成的夹角；即图中alpha ，相对于FPFH就是多了这个角度，其他基本都差不多,当然还多了一个中心点与其他各点的距离

---

• 对于官方文档中的示意图个人认为是有错误的，表述是视点与中心点的向量，示意图却是视点与其他点的向量。源码中计算使用的是中心点。
• 且官方文档中对于中心点与其他点特征计算表述易造成误解，文档表述为扩展的FPFH，但其实本质就是SPFH，易造成还需要加权计算的误解。
• 以下对官方代码进行注释，并扩展
  实现代码 VFH_estimation.cpp

int main()
{
  // load point cloud
    pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
    //    pcl::io::loadPCDFile("./data/target.pcd", *cloud);
    pcl::io::loadPCDFile("./data/bunny.pcd", *cloud);

    // estimate normals ------------------------------------------------------------- 计算法向量
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    // Object for normal estimation.
    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
    //normalEstimation.setIndices()
    normalEstimation.setInputCloud(cloud);

    // For every point, use all neighbors in a radius of 3cm.
    normalEstimation.setRadiusSearch(0.03);

    // A kd-tree is a data structure that makes searches efficient. More about it later.
    // The normal estimation object will use it to find nearest neighbors.
    pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
    normalEstimation.setSearchMethod(kdtree);
    // Calculate the normals.
    normalEstimation.compute(*normals);
    // Create the VFH estimation class, and pass the input dataset+normals to it
    pcl::VFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::VFHSignature308> vfh;
    vfh.setInputCloud (cloud);
    vfh.setInputNormals (normals);
    // alternatively, if cloud is of type PointNormal, do vfh.setInputNormals (cloud);

    // Create an empty kdtree representation, and pass it to the FPFH estimation object.
    // Its content will be filled inside the object, based on the given input dataset (as no other search surface is given).
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ> ());
    vfh.setSearchMethod (tree);

    // Output datasets
    pcl::PointCloud<pcl::VFHSignature308>::Ptr vfhs (new pcl::PointCloud<pcl::VFHSignature308> ());

    // Compute the features
    vfh.compute (*vfhs);

  // vfhs->size () should be of size 1*
  unsigned long size = vfhs->points.size();
    for (int j = 0; j < size; ++j) {
        pcl::VFHSignature308 &Signature308 = vfhs->points[j];
        float* h = Signature308.histogram;

        printf("%d: %f,%f,%f \n", j, h[1], h[2], h[3]);
    }

    // visualize normals
    pcl::visualization::PCLVisualizer viewer("PCL Viewer");
    viewer.setBackgroundColor(0.0, 0.0, 0.5);
    viewer.addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals, 1, 0.01, "normals");

    while (!viewer.wasStopped()) {
        viewer.spinOnce();
    }
    return 0;
}

其中pcl::VFHSignature308中308指，默认视点特征分割为128bin，其他每个特征分割bin数为45，现在视点特征有一个角度，中心点特征有三个角度和一个距离，则一共128+45*4=308