图像处理：像素间的一些基本关系（领域、领接性、通路、连通分量、距离）
像素间的一些基本关系
- 领域
-
- 相邻像素——4邻域
- 相邻像素——D邻域
- 相邻像素——8邻域
- 邻接性
-
- 像素间的邻接性——4邻接
- 像素间的邻接性——8邻接
- 像素间的邻接性——m邻接
- 通路
- 连通分量
- 距离
领域
相邻像素——4邻域
- 4邻域：像素p(x,y)的4邻域是： (x+1,y)；(x-1,y)；(x,y+1)；(x,y-1)
- 用N4（p）表示像素p的4邻域 ：
相邻像素——D邻域
- D邻域（ diagonal ）定义：像素p(x,y)的D邻域是：对角上的点 (x+1,y+1)；(x+1,y-1)；(x-1,y+1)；(x-1,y-1)
- 用ND（p）表示像素p的D邻域 :
相邻像素——8邻域
- 8邻域定义：像素p(x,y)的8邻域是：4邻域的点 ＋ D邻域的点
- 用N8§表示像素p的8邻域。
-N8（p）= N4（p）+ ND（p）
邻接性
- 邻接性是描述区域和边界的重要概念
- 两个像素邻接的两个必要条件是：
两个像素的位置是否相邻
两个像素的灰度值是否满足特定的相似性准则（或者是否相等）
像素间的邻接性——4邻接
- 对于具有值V的像素p和q，如果q在集合N4（p）中，则称这两个像素是4邻接的。
像素间的邻接性——8邻接
对于具有值V的像素p和q，如果q在集合N8（p）中，则称这两个像素是8邻接的 。
像素间的邻接性——m邻接
对于具有值V的像素p和q，如果:
- q在集合N4(p）中，或
- q在集合ND（p）中，并且N4（p）与N4(q)的交集为空（没有值V的像素）。则称这两个像素是m邻接的，即4邻接和D邻接的混合连通
m邻接可消除8邻接产生的二义性
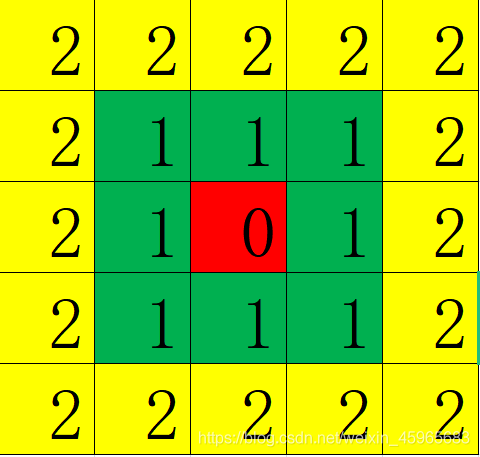
在图2中，8邻域中的中间的那个1可以有两条路到达右上角的那个1，这就是所说的二义性，这个情况在边缘检测里面是很不希望的。
如图3所示，改成m邻域以后，中间的1像素和右上角的像素是8连通的却不是m连通的，这可以从m连通的定义得到，如果用M连通从中间的1到右上角的1就只有一条路。
像素间的邻接性关系：
| 若p和q是4邻接，那么它们肯定是8邻接？ | 对 |
|---|---|
| 若p和q是8邻接，那么它们肯定是4邻接？ | 错 |
| 若p和q是4邻接，那么它们肯定是m邻接？ | 对 |
| 若p和q是m邻接，那么它们肯定是4邻接？ | 错 |
| 若p和q是8邻接，那么它们肯定是m邻接？ | 错 |
| 若p和q是m邻接，那么它们肯定是8邻接？ | 错 |
例如：
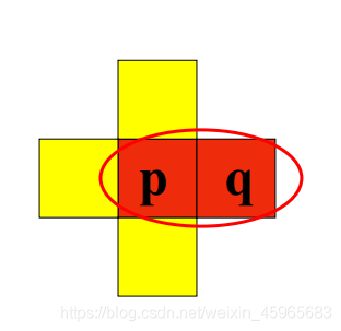
V={1},红圈所表示的两个像素，是4邻接？8邻接？还是m邻接？
答案：不是4邻接，是8邻接，是m邻接
通路
定义：一条从具有坐标(x,y)的像素p,到具有坐标(s,t)的像素q的通路。
(x0,y0),(x1,y1),…,(xn,yn)的不同像素的序列。其中，(x0,y0) = (x,y)，(xn,yn) = (s,t)，(xi,yi) 和(xi-1,yi-1)是邻接的，1 ≤ i ≤ n，n是路径的长度。如果(x0,y0) = (xn,yn) ,则该通路是闭合通路
可依据特定的邻接类型定义4通路、8通路和m通路。
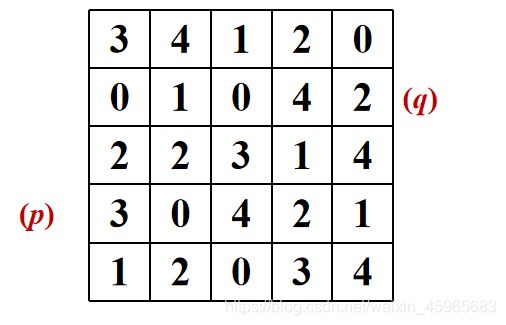
例题：
- V={2,3,4}，计算p和q之间的4通路、8通路和m通路的最短长度。
1）最短4通路,v={2,3,4}
由图可知，从p到q是无法到达的，即没有4通路，也不存在最短4通路
2）最短8通路，v={2,3,4}
最短8通路为4。即记住只要满足p的周围8个值在V值内都可以走，最短距离优先考虑斜线。
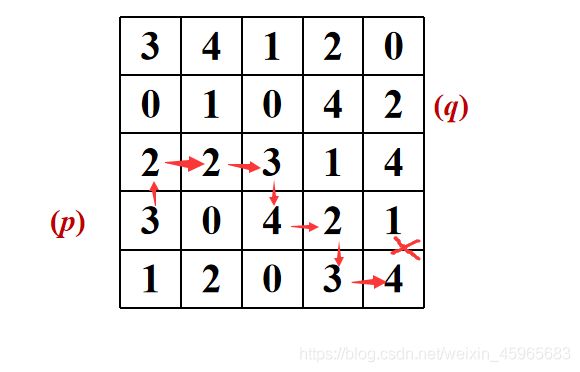
3）最短m通路 ，V={2，3，4}
最短m通路为5，即简单的说最短m通路是在最短8通路的基础上，优先考虑斜线且必须满足N4（p）与N4(q)的交集为空（没有值V的像素）。
例2：V={0,1}，计算p和q之间的最短4通路、8通路和m通路。
1）最短4通路，v={0，1}
p、q间无4通路。也可通过q的4领域值有无值v的像素快速判断是否存在4通路
2）最短8通路：
最短8通路长度为4。
3）最短m通路
最短m通路为5
| 若p和q之间存在4通路，则两者之间必存在m通路 | 对 |
|---|---|
| 若p和q之间存在m通路，则两者之间必存在4通路 | 错 |
| 若p和q之间存在m通路，则两者之间必存在8通路 | 对 |
| 若p和q之间存在8通路，则两者之间必存在m通路 | 对 |
| 若p和q之间存在8通路，则两者之间必存在4通路 | 错 |
| 若p和q之间存在4通路，则两者之间必存在8通路 | 对 |
连通分量
令S是图像中的一个像素子集。如果在S中全部像素之间存在一个通路，则可以说p和q在S中是连通（connected）的。对于S中的任何像素p，S中连通到该像素的像素集称为S的连通分量。如果S仅有一个连通分量，则集合S称为连通集(connected set)。
例：计算所给图中的连通域个数（分别用4连通和8连通求）。
4连通的连通域有6个，分别是：
{A,B}、{C}、{D，E}、{F,G,H}、{I}、{J，K}
8连通的连通域有2个，分别是：
{A,B,C,D,E}、{F,G,H,I,J,K}
距离
像素p(x,y)和q(s,t)间的欧式距离定义如下：
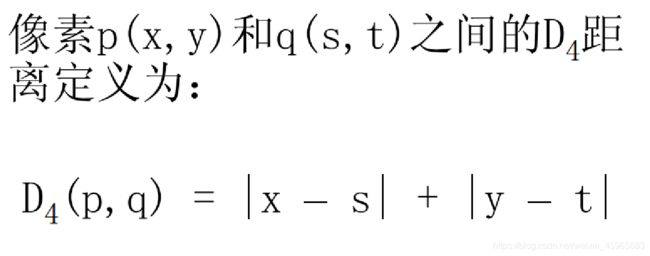
1）D4距离举例
具有与(x,y)距离小于等于某个值r的那些像素形成一个菱形
例如，与点(x,y)（中心点0）D4距离小于等于2的像素，形成下边固定距离的轮廓
具有D4 = 1的像素是(x,y)的4邻域
D8距离举例
对比D4距离，D8距离具有与(x,y)距离小于等于某个值r的那些像素形成一个正方形
例如，与点(x,y)（中心点0）D8距离小于等于2的像素，形成下边固定距离的轮廓
具有D8 = 1的像素是(x,y)的8邻域
