机器学习之混淆矩阵 confusion_matrix
1.这里介绍由 sklearn.metrics.ConfusionMatrixDisplay 所给出的关于混淆矩阵的一个小例子,来进行理解混淆矩阵及如何应用混淆矩阵来对数据进行分析
2.先了解混淆矩阵的一些基本信息,这里规定正类为1,负类为0
TP(True Positives): 预测为1,而真实的也为1 (即正类判断为正类,1判断为1)
TN(True Negatives): 预测为0,真实的也为0 (即负类判断为负类,0判断为0)
FP(False Positives): 预测为1,真实的为0 (即负类判断为正类,将0判断为了1)
FN(False Negatives): 预测为0,真实为1 (即正类判断为负类,将1判断为了0)
| 样本总数=25 | 预测为:0 | 预测为:1 | |
| 真实为:0 | TN = 12 | FP = 1 | 真实的0总数:13 |
| 真实为:1 | FN = 2 | TP = 10 | 真实的1总数:12 |
| 预测的0总数:14 | 预测的1总数:11 |
上方表格中,说明一下FN = 2 ,即表示预测为0的样本总的有14个,但是其中有2个样本咱预测成了0不过其真实的情况是为1,所以得到了FN = 2,即将本来是1的预测成了0(正类预测成了负类)。
为了便于理解,还可以将1理解成患病的情况,0是没病的情况,那么上面FN=2,则可理解成,将本来是患病的2个人预测成了没病,所以自然预测出问题了,他俩本来有病,但计算机预测他俩没病。
这个预测的数据,并非人为的凭空捏造,而是通过相关模型的建立及训练后,传入相关测试数据后,得到的预测数据。
而我们会想如果预测的数据和真实的数据情况一样的情况呢,即假设咱建立的模型很牛掰,预测的很准达到了100%正确,那么TN、FP、FN、TP的取值又该如何呢?即如下表情况:我们规定其真实的0的个数和上表一样还是13个,真实的1的个数仍旧为12,然后预测情况如下:
| 样本总数=25 | 预测为:0 | 预测为:1 | |
| 真实为:0 | 13 | 0 | 真实的0总数:13 |
| 真实为:1 | 0 | 12 | 真实的1总数:12 |
| 预测的0总数:13 | 预测的1总数:12 |
可以看到预测情况和真实的情况一样,即这种情况毫无疑问,预测准确率达到了100%,当然一般情况下,预测能力可达不到100%正确。
除上述外还需了解召回率(recall score)的相关信息,可从sklearn.metrics.recall_score 中进行了解,即使用TN、FP、FN、TP的相关值来计算的一个分数,进而评估该预测效果
3.接下来了解通过代码及运行结果来进行相关信息的理解及应用
3.1 基于SVC的方式来进行训练及预测
# 混淆矩阵 confusion matrix
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics._classification import recall_score
X, y = make_classification(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y,random_state=0)
print("真实的 Y值:",y_test)
# SVC 方式
clf = SVC(random_state=0)
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
print("预测的 Y值:",predictions)
# SVC
#Y: [1 1 1 0 0 1 1 0 1 1 1 0 0 0 0 1 0 0 1 1 0 0 1 0 0]
#p: [1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 0 0 1 1 1 0 1 0 0]
# x x x
cm = confusion_matrix(y_test, predictions)
disp = ConfusionMatrixDisplay(confusion_matrix=cm)
r = recall_score(y_test,predictions,average='macro')
print("\n","recall score:" , r)
disp.plot()
plt.show()
控制台输出:recall score = 0.8782051282051282
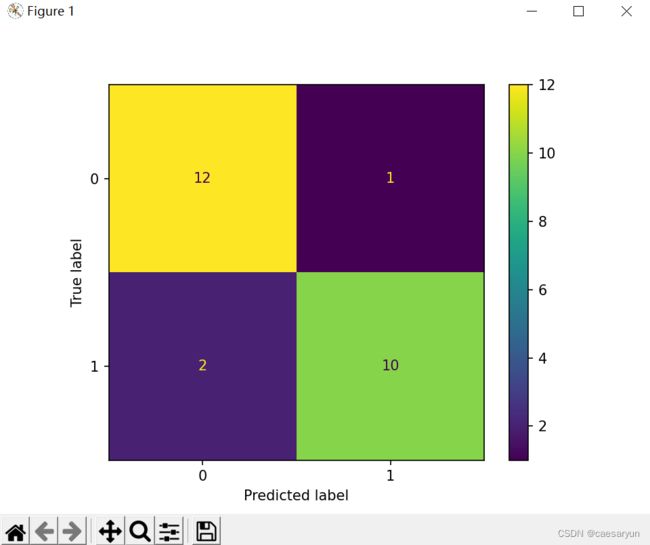
混淆矩阵图像:
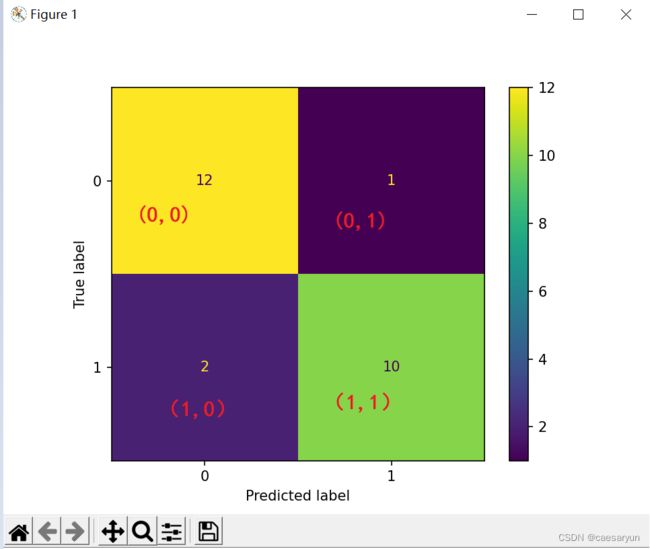
为了方便理解,不妨将混淆矩阵的各个模块添加上坐标,所以可以看到下图的各个模块坐标,坐标为(0,0)的模块样本数量有12个,(0,1)的有1个,(1,0)的有2个,(1,1)的有10个
首先通过对控制台输出的真实的 Y 值及预测的Y值进行分析,可以看到下图中打上红叉的地方,预测的Y值与真实值并不一样,所以可以看到混淆矩阵图上(1,0)的地方有2个,其代表的意思就是预测为0但实际为1的样本数量有2个,即 FN = 2;
又有(0,1)的模块有1个样本,即 FP = 1,表示为预测为 1但实际上是 0(将负类预测成了正类,0预测成了1);
又有(0,0)的模块为12个,即 TN = 12,表示为预测为0,真实的也为0的有12个样本(负类预测成负类,0预测成了0);
之后有(1,1)的模块为10个,即 TP = 10,表示为预测成1,真实的也为1的有10个样本(正类预测成正类,1预测成了1)。
3.2 基于逻辑回归的方式训练及预测
# 添加如下代码,且将SVC方式注释掉使用逻辑回归方式即可
from sklearn.linear_model import LogisticRegression
# SVC 方式
# clf = SVC(random_state=0)
# 逻辑回归方式
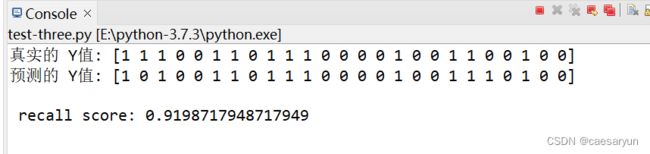
clf = LogisticRegression(random_state=0)可以发现recall score 分数较SVC的提高了些
可以发现对比之前的混淆矩阵,逻辑回归方式,(1,1)即 TP = 11,从TP = 10 提高到了 11,略有上升。
3.3 线性回归的方式训练及预测
# 添加线性回归的库,即调用线性回归的代码
from sklearn.linear_model import LinearRegression
# SVC 方式
# clf = SVC(random_state=0)
# 逻辑回归方式
# clf = LogisticRegression(random_state=0)
# 采用线性回归
clf = LinearRegression()
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
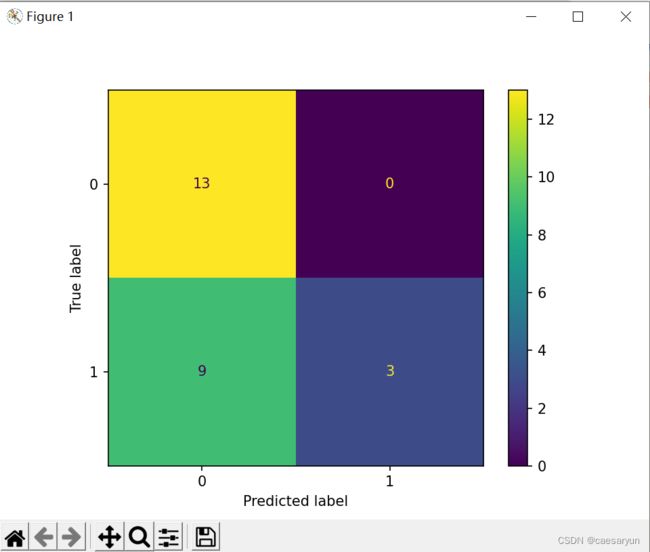
predictions = predictions.astype(int) # 将预测数据转为int类型可以看到线性回归方式进行预测效果有些不太理想,recall score 降低了很多
从混淆矩阵来看,预测的效果,在预测为1且实际为1时的情况即TP的值下降了许多,该方式进行预测有点不太理想。
4.以上便为混淆矩阵的一些简单理解,总体来说,混淆矩阵表示相关数据情况,还是比较直观的。