Normalized Glow论文阅读

论文链接：Glow: Generative Flow with Invertible 1×1 Convolutions

摘要

基于流的生成模型在概念上很有吸引力，因为精确对数似然的可处理性，准确潜变量推理的可处理性，以及训练和合成的并行化。本文中提出了Glow，这是一种使用可逆1×1卷积的简单生成流。使用该方法证明了标准基准在对数似然方面的显着改进。也许最引人注目的是，证明了针对普通对数似然目标优化的生成模型能够有效地合成和处理大图像的逼真外观。

简介

机器学习领域的两个主要未解决问题是（1）数据效率：从少数数据点学习的能力，如人类； (2) 泛化：对任务或其上下文变化的鲁棒性。例如，当输入与其训练分布不同时，AI系统通常根本无法工作。生成模型是机器学习的一个主要分支，它有望通过以下方法克服这些限制:(1)学习现实世界模型，潜在地允许代理在与世界进行实际交互之前在世界模型中进行计划;(2)学习输入的有意义的特征，同时需要很少或不需要人类监督或标记。由于这些特征可以从大型无标签数据集中学习，而且不一定是特定于任务的，基于这些特征的下游解决方案可能更健壮，数据效率更高。在本文中，除了中间应用程序之外，还致力于通过改进生成模型的最先进技术来实现这一终极愿景。

生成式建模通常涉及一项极具挑战性的任务，即在非常高维的输入数据中建模所有依赖项，通常以全联合概率分布的形式指定。由于这种联合模型潜在地捕获了数据中存在的所有模式，因此精确生成模型的应用几乎是无穷无尽的。即时应用包括语音合成、文本分析、半监督学习和基于模型的控制。

生成建模的学科近年来在能力上经历了巨大的飞跃，主要是基于可能性的方法和生成对抗网络(GANs)。基于可能性的方法可分为三类:

• 自回归模型：此类方法的优点是简单，但缺点是合成的并行性有限，因为合成的计算长度与数据的维数成正比;这对于较大的图像或视频尤其麻烦
• 变分自编码器/VAEs：优化数据的对数似然的下界；变分自编码器在训练和合成的并行性方面具有优势，但在优化方面相对具有挑战性
• 基于流的生成模型首次在NICE中描述，并在RealNVP中扩展

与GANs和VAEs相比，基于流的生成模型迄今在研究社区中获得的关注很少。基于流的生成模型的一些优点包括:

• 精确的潜变量推理和对数似然评估：在VAEs中，只能近似地推断出与数据点相对应的潜在变量的值。GANs根本没有编码器来推断潜在值。在可逆生成模型中，这可以精确地完成而无需近似。这不仅可以导致准确的推理，还可以优化数据的精确对数似然，而不是下限
• 高效推理和高效合成：自回归模型，例如 PixelCNN，也是可逆的，但是这些模型的合成很难并行化，并且在并行硬件上通常效率低下。像 Glow（和 RealNVP）这样的基于流的生成模型可以有效地并行化推理和合成
• 为下游任务提供有用的潜在空间：自回归模型的隐含层具有未知的边际分布，使得对数据进行有效的操作变得更加困难。在GANs中，数据点通常不能直接表示在潜在空间中，因为它们没有编码器，可能没有对数据分布的完全支持。这不是可逆生成模型和VAEs的情况，它们允许各种应用程序，如数据点之间的插值和对现有数据点的有意义的修改
• 显著的内存节省潜力：在可逆神经网络中，计算梯度需要的内存量是恒定的，而不是线性的

图1 Glow模型中采样的合成名人

背景：基于流的生成模型

设x为未知真实分布的高维随机向量，$x～p^{\ast }(x)$。搜集数据集$D$，选择一个带有参数$\theta$的模型$p_{\theta }(x)$。在离散数据x的情况下，对数似然目标等于最小化：
$$L(D)=\frac{1}{N}\sum _{i=1}^N-\log p_{\theta }(x^{(i)})$$
在连续数据 x 的情况下，最小化以下内容：
$$L(D)\simeq \frac{1}{N}\sum _{i=1}^N-\log p_{\theta }({\tilde{x}}^{(i)})+c$$
其中${\tilde{x}}^{(i)}=x^{(i)}+u,u\backsim U(0,a),c=-M\cdot \log a$，$a$由数据的离散化程度决定，$M$是$x$的维数。以上两个公式的目标都以 nats 或 bits 为单位测量预期的压缩成本；优化是通过使用小批量数据的随机梯度下降来完成的。

在大多数基于流的生成模型中，生成过程定义为：
$$z\backsim p_{\theta }(z)$$ $$x=g_{\theta }(x)$$

其中$z$是潜在变量，$p_{\theta }(z)$具有（通常是简单的）易处理的密度，例如球形多元高斯分布：$p_{\theta }(z)=N(z;0,I)$。函数$g_{\theta }(..)$是可逆的，也称为双射，因此给定数据点$x$，潜在变量推断由$z=f_{\theta }(x)=g_{\theta }^{-1}(x)$完成。

f（同样，g）由一系列变换组成的函数：$f=f_1◦f_2◦\cdot \cdot \cdot ◦f_K$ ，因此$x$和$z$之间的关系可以写为：
$$x\stackrel{f_1}{⟷}{h}_1\stackrel{f_3}{⟷}{h}_2\cdot \cdot \cdot \stackrel{f_K}{⟷}z$$

这种可逆变换序列也称为（归一化）流。结合上述等式，给定数据点的模型的概率密度函数（pdf）可以写成：

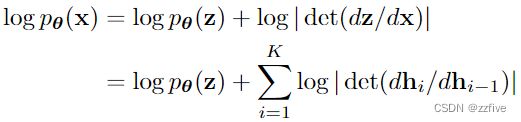
其中为了简洁起见，定义$h_0\triangleq x,h_K\triangleq z$。标量值$\log |det(d{h}_i/d{h}_{i-1})|$是雅可比矩阵行列式$(d{h}_i/d{h}_{i-1})$的绝对值的对数，也称为对数行列式/log-determinant。该值是在变换$f_i$下从$h_{i-1}$到$h_i$时对数密度的变化。虽然它看起来很吓人，但对于某些转换选择，它的值计算起来非常简单。基本思想是选择雅可比$d{h}_i/d{h}_{i-1}$是三角矩阵的变换。对于这些转换，对数行列式很简单：
$$\log |det(d{h}_i/d{h}_{i-1})|=sum(\log |diag(d{h}_i/d{h}_{i-1})|)$$
其中sum()取所有向量元素的和，log()取元素的对数，diag()取雅可比矩阵的对角线

提出的生成流

提出了一个新的流程，建立在提出的NICE和RealNVP流程的基础上。它由一系列的流程步骤组成，结合在一个多尺度的架构中;参见图2。流动的每一步都由$actnorm$和可逆的1 × 1卷积和耦合层组成。该流程与多尺度架构相结合;由于空间限制，参考RealNVP了解更多细节。该体系结构的深度为流K，层数为L(图2)。

图2 Glow整体架构

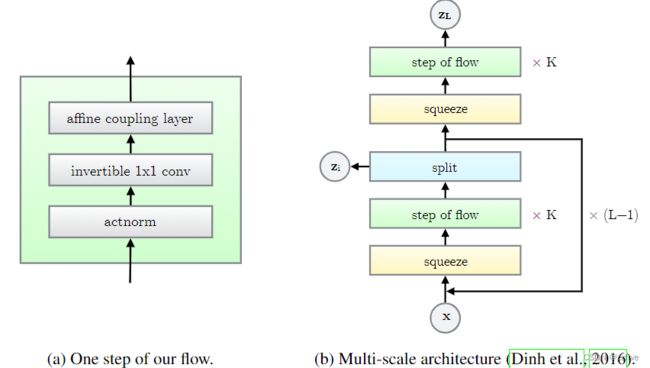
Actnorm：具有数据相关初始化的缩放和偏差层

RealNVP的作者建议使用批归一化来缓解在训练深度模型时遇到的问题。然而，由于批归一化所增加的激活噪声的方差与每个GPU或其他处理单元(PU)的小批量大小成反比，所以众所周知，每PU的小批量大小会降低性能。对于较大的图像，由于内存限制，使用每个PU的小批处理大小为1；提出了一个actnorm层(用于激活归一化)，它使用每个通道的尺度和偏差参数执行激活的仿射转换，类似于批处理归一化。这些参数被初始化，使得给定初始小批数据，每个通道的actnorm后激活具有零平均值和单位方差。这是一种依赖于数据的初始化形式。初始化后，尺度和偏差被视为与数据无关的常规可训练参数。（训练第一个batch时模型参数的初始化的均值和方式是要通过第一个batch里的数据计算的，不是随机初始化，后续的batch就是常规的训练更新）

可逆的1×1卷积

NICE提出了一个包含等效置换的流，该置换颠倒了通道的顺序。本文建议用（学习的）可逆1×1卷积替换这个固定排列，其中权重矩阵被初始化为随机旋转矩阵。请注意，输入和输出通道数相等的1 × 1卷积是置换操作的推广。

h × w × c张量$h$与c × c权重矩阵$W$的可逆1 × 1卷积的对数行列式可以直接计算:

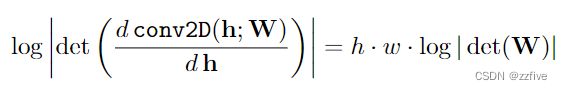
计算或微分$det(W)$的成本为$O(c^3)$，通常与计算conv2D(h;W)的成本相当，即$O(h\cdot w\cdot c^2)$。将权重$W$初始化为随机旋转矩阵，其对数行列式为0；经过一个 SGD 步骤后，这些值开始从0发散。

LU分解

通过在LU分解中直接参数化W, $det(W)$的计算成本可以从$O(c^3)$减少到$O(c)$:
$$W=PL(U+diag(s))$$
其中P是置换矩阵，L是对角线上为1的下三角矩阵，U是对角线上为0的上三角矩阵，s是向量。对数行列式简化为：
$$\log |det(w)|=sum(\log |s|)$$
对于较大的c，计算成本的差异将变得显著，尽管对于本文实验中的网络，没有测量到wallclock计算时间的很大差异。在这个参数化过程中，首先对一个随机旋转矩阵W进行采样，然后计算相应的P值(保持固定)和相应的L、U和s的初始值(经过优化)，从而初始化参数。

仿射耦合层

NICE中引入的仿射耦合层是一种强大的可逆变换，其中正函数、反函数和对数行列式计算效率高。见表1所示，加性耦合层是s = 1和log-行列式为0的特殊情况。

表1 提出的流的三个主要组成部分，它们的逆，以及它们的对数行列式。这里，x表示层的输入，y表示层的输出。x和y都是形状为[h × w × c]的张量，具有空间维度(h, w)和通道维度c。使用(i, j)，将空间指标表示为张量x和y。函数NN()是一个非线性映射，如ResNets 和RealNVP中的(浅)卷积神经网络

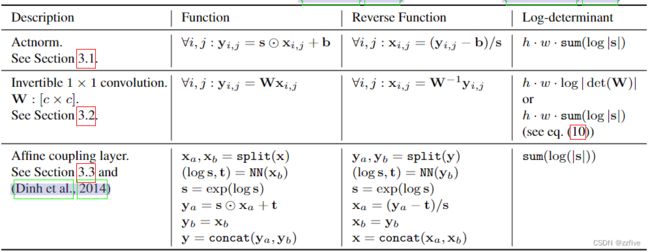
零初始化

用零初始化每个NN()的最后一个卷积，这样每个仿射耦合层最初执行一个恒等函数；本文发现这有助于训练非常深入的网络。

分割和连接

在NICE中，split()函数将输入张量沿着通道维度分成两半，而concat()操作则执行相应的反向操作:将输入张量拼接成单个张量。在RealNVP中，引入了另一种类型的拆分：沿空间维度使用棋盘格图案。在这项工作中，仅沿通道维度执行拆分，从而简化了整体架构。

置换

上述流程的每个步骤之前都应该有某种变量排列，以确保在足够的流程步骤之后，每个维度都可以影响其他所有维度。在NICE中具体完成的排列类型相当于在执行加性耦合层之前简单地反转通道（特征）的顺序。另一种方法是执行（固定）随机排列。可逆 1x1 卷积是这种排列的泛化。在实验中比较了这三种选择。

相关工作

这项工作建立在NICE和RealNVP中提出的想法和流程之上；整篇论文都与这项工作进行了比较。在MAF中，作者提出了一种基于IAF的生成流 ；然而，由于MAF的合成是不可并行的，因此效率低下，将其从比较中省略。自回归 (AR) 模型的合成同样是不可并行的。使用 AR 模型，高维数据的合成通常需要几个数量级的时间。在当前硬件上，使用本文提出最大的模型对 256 × 256 图像进行采样只需不到一秒的时间。

与基于可能性的方法相比，GANs 最有名的是其合成大型和真实图像的能力。GANs的缺点是普遍缺乏潜在空间编码器，普遍缺乏对数据的充分支持，难以优化，难以评估过拟合和泛化。

定量实验

通过比较提出的新Flow与 RealNVP 的来开始实验。然后，将模型应用于其他标准数据集，并将对数似然与以前的生成模型进行比较。有关优化的详细信息，请参见附录。在实验中，让每个 NN() 具有三个卷积层，其中两个隐藏层具有 ReLU 激活函数和 512 个通道。第一个和最后一个卷积是3×3，而中心卷积是1×1，因为它的输入和输出都有大量的通道，与第一个和最后一个卷积相比。

使用可逆1×1卷积的优增益

选择前文中描述的体系结构，并考虑信道变量的排列的三种变化—RealNVP中描述的反转操作、固定随机排列和可逆的1 × 1卷积。比较了只有附加耦合层的模型和具有仿射耦合的模型。如前所述，使用依赖于数据的初始化来初始化所有模型，该初始化规范化了每一层的激活。所有模型训练K = 32, L = 3。1 × 1卷积模型的参数量增加0.2%，可以忽略不计。

比较CIFAR-10数据集上的平均负对数似然(每维位)，保持所有训练条件不变，并在三个随机种子上取平均值，结果如图3所示。正如所看到的，对于加性耦合和仿射耦合，可逆的1 × 1卷积实现了更低的负对数似然，并且收敛得更快。仿射耦合模型也比加性耦合模型收敛更快。注意到可逆1 × 1卷积模型的壁钟时间只增加了≈7%，因此计算效率也很高。

图3 三种变体的比较——RealNVP 中描述的逆向操作、固定随机排列和本文提出的可逆1×1卷积，具有加法耦合层（左）与仿射耦合层（右）。用不同的随机种子绘制了三次运行的平均值和标准差

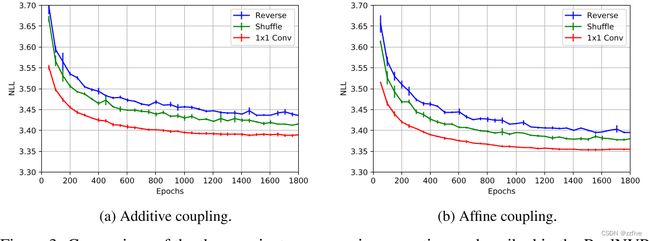
与RealNVP在标准基准测试上的比较

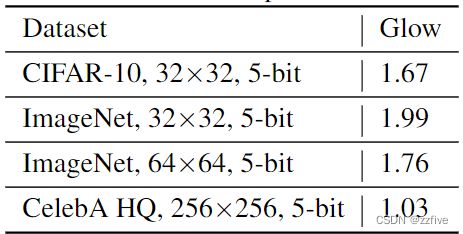
除了排列操作之外，RealNVP体系结构还有其他不同之处，例如空间耦合层。为了验证提出的架构在整体上与RealNVP架构具有竞争力，在各种自然图像数据集上比较了模型。特别地，比较了CIFAR-10、ImageNet和LSUN数据集。遵循与RealNVP相同的预处理。对于Imagenet，使用Imagenet的32 × 32和64 × 64的下采样版本，而对于LSUN，下采样到96 × 96，并采用64 × 64的随机作物。还包括在定性实验中使用256 × 256 CelebA HQ训练的模型的位/维数。如表2所示，提出的模型在所有数据集上都取得了显著的改进。

表2 与 RealNVP 相比，Glow模型的每个维度的最佳结果

定性实验

在高分辨率数据集上研究模型的定性方面；选择CelebA- hq数据集，该数据集由来自CelebA数据集的30000张高分辨率图像组成，并训练与上面相同的架构，但现在训练分辨率为$256^2$、$K=32$和$L=6$的图像。为了以轻微降低颜色保真度为代价提高视觉质量，在5位图像上训练模型。我目标是研究提出的模型是否可以缩放到高分辨率，产生真实的样本，并产生有意义的潜在空间。由于设备内存限制，在这些分辨率下，使用每个PU大小为1的小批处理，并使用梯度检查点。在未来，可以利用模型的可逆性，使用与深度无关的恒定内存量。

与基于可能性的生成模型的早期工作（Image Transformer）一致，发现从降低温度模型中采样通常会产生更高质量的样本。当使用温度$T$采样时，从分布$p_{\theta ,T}(x)\propto (p_{\theta }(x){)}^{T^2}$中采样。在加性耦合层的情况下，这可以通过将$p_{\theta }(z)$的标准偏差乘以$T$的一个因子。

合成和插值

图4显示了从我Glow模型中获得的随机样本。对于非自回归似然模型，图像的质量非常高。为了看看插值效果如何，取一对真实的图像，用编码器对它们进行编码，然后在潜伏期之间进行线性插值以获得样本。图5的结果显示，生成器分布的图像流形非常平滑，几乎所有的中间样本看起来都像真实的人脸。

图4 模型中的随机样本，温度为 0.7

图5 真实图像在潜在空间中的线性插值

语义操作

考虑修改图像的属性。为此，使用 CelebA 数据集中的标签。每个图像都有一个二分类标签，对应于微笑、金发、年轻等属性的存在与否。这为每个属性提供了 30000 个二分类标签。计算具有属性的图像的平均潜在向量$z_{pos}$和没有属性的图像的$z_{neg}$，然后使用差异$(z_{pos}-z_{neg})$作为操作方向。请注意，这是一个相对较少量的监督，并且是在模型训练之后完成的（训练时没有使用标签），因此对于各种不同的目标属性来说非常容易，结果如图 6 所示。

图6 人脸属性的操作。每一行都是通过沿着与属性对应的向量对图像的潜在代码进行插值得到的，中间的图像是原始图像

温度和模型深度的影响

图7 样本来自在温度为0.875的5位LSUN卧室中训练的模型。分辨率分别为64、96和128。对于128 × 128和96 × 96版本，对原始图像进行中心裁剪，并进行下采样。对于64 × 64版本，像RealNVP所做的那样，从96 × 96的下采样图像中随机提取作物

---

图8显示了样品质量和多样性随温度的变化情况。最高温度的图像有噪声，可能是由于高估了数据分布的熵，因此选择0.7的温度作为样本多样性和质量的最佳点。图9显示了模型深度如何影响模型学习长期依赖关系的能力。

图8 温度变化的影响。从左到右分别为0、0.25、0.6、0.7、0.8、0.9、1.0温度下的样品

图9 左边是浅模型，右边是深模型。浅模型L = 4层，深模型L = 6层

结论

出了一种新的流类型，即Glow，并展示了在标准图像建模基准上的对数似然性方面改进的量化性能。此外证明，当对高分辨率的人脸进行训练时，模型能够合成真实的图像。当时Glow模型是文献中第一个可以有效合成高分辨率自然图像的基于似然的模型。

附录

A.附加的定量结果

表3 测试集上以每维位数为单位的量化结果

B.可逆1×1卷积的简单python实现

# Invertible 1x1 conv
def invertible_1x1_conv(z, logdet, forward=True):
	# shape
	h, w, c = z.shape[1:]
	# sample a random orthogonal matrix to initialise weights
	w_init = np.linalg,qr(np.random,.randn(c, c))[0]
	w = tf.get_veriable("w", initializer=w_init)
	# computer log determinant
	dlogdet = h * w * tf.log(abs(tf.matrix_determinant(w)))

	if forward:
		# forward computation
		_w = tf.reshape(w, [1, 1, c, c])
		z = tf.nn.conv2d(z, _w, [1, 1, 1, 1], 'SAME')
		logdet += dlogdet
		return z, logdet
	else:
		# reverse computation
		_w = tf.matrix_inverse(w)
		_w = tf.reshape(_w, [1, 1, c, c])
		z = tf.nn.conv2d(z, _w, [1, 1, 1, 1], 'SAME')
		logdet -= dlogdet
		return z, logdet

C.优化细节

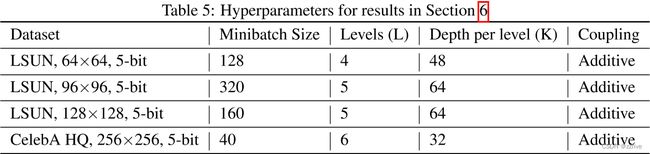
使用 Adam 优化器，α = 0.001，默认的${\beta }_1和{\beta }_2$。在定量实验中，使用了以下超参数（表 4）。

表4 定量实验结果的超参数

在定性实验中，我使用了以下超参数（表 5）：

表5 定性实验结果的超参数

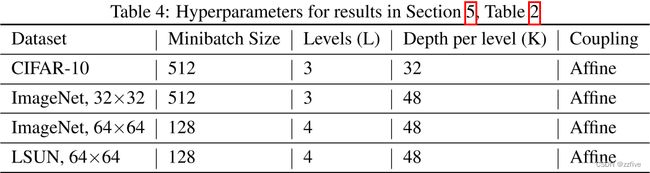
D.定性实验的额外样本

对于类条件CIFAR-10和32×32 ImageNet样本，使用与定量实验相同的超参数，但在最顶层具有类相关的先验；还增加了一个分类损失来预测编码器最后一层的分类标签，其权重λ = 0.01，结果如图10所示。

图10 分别在5位CIFAR-10和32 × 32 ImageNet上分类条件样本。温度0.75

E.定量实验的额外样本

为了与其他工作进行直接比较，数据集按照RealNVP的方法进行了预处理。结果见图11和图12。

图11 样本分别来自8位，64×64 LSUN卧室，教堂和塔。温度1.0

图12 来自带有仿射耦合层的无条件模型的样本在温度为1.0的CIFAR-10数据集上训练