【图神经网络】异构时间图卷积网络HTGCN——用于社区检测
【图神经网络】异构时间图卷积网络——用于社区检测
- 论文地址:
- 摘要:
- 研究关键点:
- 核心解决方案:
- 几个定义:
-
- 1. 异构图:
- 2. 异构图的邻接矩阵:
- 3. Meta-Path(元路径):
- 4. 问题陈述:
- HTGCN算法:
-
- 1. 异构GCN组件:
- 2. 残差压缩聚合组件(ResCAC):
-
- 2.1 元路径:
- 2.2 Hadamard积:
- 2.3 压缩:
- 3. 伪代码:
- 社区检测:
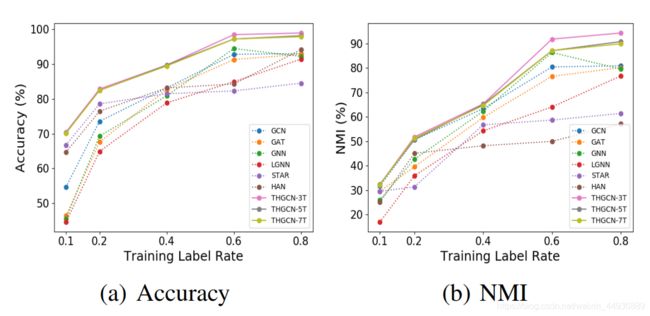
- 实验结果:
论文地址:
《Heterogeneous-Temporal Graph Convolutional Networks: Make the Community Detection Much Better》
摘要:
![]()
社区检测从本质上讲,真实世界的图形数据包含各种随时间动态变化的特性、节点和边缘类型,这使得大多数现有的社区检测方法(静态)无效。
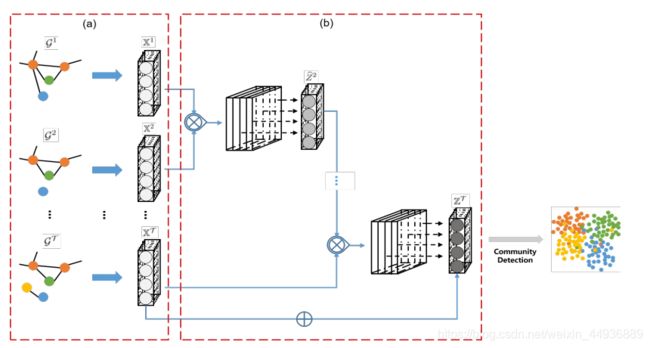
为了解决这些问题,本文提出了混合时间图卷积网络(称之为HTGCN)来从混合时间图中检测社区。作者首先设计了一个异构GCN组件来获取每个异构图在每个时间步长的特征表示。然后,提出一个残差压缩聚合组件来表示“变化”社区的“动态”特征,然后将这些特征与当前图中提取的“静态”特征进行聚合。
即:
- 通过异构GCN获取异构图在每个时间步长的特征表示;
- 通过残差压缩聚合组件来表示“变化”社区的“动态”特征;
- 最后将动态特征与静态特征进行融合;
研究关键点:
关键的研究难点在于不同时间步长的异质性图中群落的动态演化。因此,除了当前图中呈现的“静态”社区外,我们还需要学习有效的动态特征表示,以便从一系列图中发现“不同”的社区。
显然,所需的特征表示应该包括两部分。其中一部分表示从当前图中提取的“静态”特征。另一部分表示“动态”特征,应该从不同时间步骤的图之间的交互中提取。这样做,不可避免地会产生一个大的稀疏特征表示空间,需要较高的计算代价。因此,如何进一步减少高计算量也是一个问题。
核心解决方案:
为了很好地解决上述研究难题,作者(首次)提出了用于社区检测任务的异构时态图卷积网络(HTGCN)。
- 作者首先定义计算异构邻接矩阵的计算方法,然后分别嵌入每个瞬时图的空间结构信息和节点特征。
- 然后,作者提出了残余压缩聚合组件(ResCAC)。该组件首先利用元路径从几个连续图中对可能属于同一社区的异质性相关节点进行采样。该采样步骤具有保存时间共同体信息的优点。然后,该组件交互节点特性并压缩这些交互特性表示。
- 为了同时表示时不变群落和进化群落的特征,作者还将当前图的特征与压缩的时间特征进行聚合,并通过残差连接的线性层进行聚合。
- 最后,提出了修正的社区检测损失函数。
几个定义:
1. 异构图:
假设图 G = ( V , E ) G=(V,E) G=(V,E), T V T_V TV和 T E T_E TE分别代表顶点类别和边类别,如果: ∣ T V ∣ + ∣ T E ∣ > 2 |T_V|+|T_E|>2 ∣TV∣+∣TE∣>2,则 G G G为异构图。
∣ T V ∣ + ∣ T E ∣ > 2 |T_V|+|T_E|>2 ∣TV∣+∣TE∣>2,为异构图。
2. 异构图的邻接矩阵:
异构图 G G G的邻接矩阵定义为: A H G = { A i j ∣ i ∈ [ 1 , m ] , j ∈ [ 1 , n ] } A_{HG}=\lbrace A_{ij}|i\in [1, m], j\in[1,n]\rbrace AHG={Aij∣i∈[1,m],j∈[1,n]}。
其中: m = ∣ T V ∣ m=|T_V| m=∣TV∣, n = ∣ T E ∣ n=|T_E| n=∣TE∣。
注意, A i j A_{ij} Aij表示固定节点类型 i i i 和边类型 j j j 所生成的同构图的邻接矩阵,因此,异构图 G G G的度矩阵可定义为 D H G D_{HG} DHG = d i a g ( D i i ) diag(D_{ii}) diag(Dii),其中 D i i = P j A i j D_{ii} = P_j A_{ij} Dii=PjAij。即将两个相同类型 i i i 的节点之间不同类型 j j j 的边数相加。
3. Meta-Path(元路径):
元路径最初用于捕获异构节点和边缘之间的关系。一般来说,元路径 δ δ δ可以定义为:

其中 a i a_i ai代表不同顶点, e i e_i ei代表不同边。
例如,绿色对应顶点为P,边类型对应: A ⟶ w r i t e P A\stackrel{write}{\longrightarrow}P A⟶writeP, P ⟶ w r i t e d A P\stackrel{writed}{\longrightarrow}A P⟶writedA, P ⟶ p u b l i s h e d C P\stackrel{published}{\longrightarrow}C P⟶publishedC。
4. 问题陈述:
假设 G \mathbb{G} G是一些时序图数据的集合,即: G = ( g 1 , g 2 , … , g T ) \mathbb{G}=(g^1,g^2,…,g^T) G=(g1,g2,…,gT),其中 T T T是时间步长。
假设 g t = ( V t , A H G t , X t , T , C t ) g^t=(V^t,A^t_{HG},X^t,T,C^t) gt=(Vt,AHGt,Xt,T,Ct)是在 t t t 时刻的异构图, V t V^t Vt是 g t g^t gt的顶点集, X t ∈ R N t × D t X^t\in\mathbb{R}^{N^t×D^t} Xt∈RNt×Dt代表顶点集 V t V^t Vt的特征矩阵, N t N^t Nt代表 g t g^t gt的顶点数, D t D^t Dt是 X t X^t Xt的特征维度,并且 C t C^t Ct={1,…,C}代表了社区的标签集合。
那么正高社区检测任务就变成了在 g t g^t gt中通过有监督的方式,预测每个顶点的社区标签,其最小化目标损失函数定义如下:

HTGCN算法:
1. 异构GCN组件:
为了嵌入空间结构信息和节点特征,作者提出了这种异构GCN组件,它将节点特征与所有one-hop邻居的特征进行卷积。卷积操作可以定义为:

其中:

且 W i W_i Wi是权重矩阵, X i X_i Xi是第 i i i 层的特征矩阵, σ \sigma σ是 ReLU 激活函数, A H G A_{HG} AHG是异构邻接矩阵,一般用于表示特定节点或边类型的节点之间的邻域关系。
这个组件的输出表示为: X ∈ R N × D \mathbb{X}\in\mathbb{R}^{N×D} X∈RN×D。
2. 残差压缩聚合组件(ResCAC):

在获得异构GCN组件生成的 X \mathbb{X} X后,提出的 ResCAC 本质上是学习能够很好地表示隐藏群落进化模式的特征表示。
2.1 元路径:
首先利用元路径从每个瞬时图中采样异质性相关的节点。直观地看,虽然节点在每个时间步长都可能加入或离开异构图,但仍然存在一些时间上是不变节点。这些保留的节点自然成为不同时间步骤的图之间的“纽带”。
因此,作者提出利用元路径对异质相关节点进行采样。
例如,根据元路径 δ : P → A → P δ:P→A→P δ:P→A→P,我们可以筛选出 g t − 1 g^{t-1} gt−1和 g t g^t gt中存在的作者顶点(类型为A)。然后将嵌入的论文顶点(类型为P)分别采样到两个特征矩阵中,即图中中上部分黄色点矩形所表示的是同一作者对两个连续图特征矩阵,即 X δ t X_{\delta}^t Xδt(对应 g t g^t gt中的 A → P A→P A→P中的 P P P)和 Z δ t − 1 Z_{\delta}^{t-1} Zδt−1(对应 g t − 1 g^{t-1} gt−1中的 P → A P→A P→A中的 P P P)。
2.2 Hadamard积:
其次,分别从特征矩阵 X t \mathbb{X}^t Xt和 Z t − 1 \mathbb{Z}^{t-1} Zt−1中提取这些节点的两个子特征矩阵,对其进行Hadamard积运算,得到一个保留“变化”社区交互特征的三维张量。利用 X δ t X_{\delta}^t Xδt和 Z δ t − 1 Z_{\delta}^{t-1} Zδt−1乘例,给出的Hadamard积和拼接后的特征矩阵为:

其中 2 ≤ t ≤ T 2\leq t\leq T 2≤t≤T, H δ t \mathbb{H}^t_{\delta} Hδt是一个三维张量, X δ t ∈ X t X_{\delta}^t\in\mathbb{X}^t Xδt∈Xt和 Z δ t − 1 ∈ Z t Z_{\delta}^{t-1}\in\mathbb{Z}^t Zδt−1∈Zt分别表示异构GCN组件在时间步长 t t t和ResCAC在时间步长 t − 1 t-1 t−1时生成的节点的特征表示, ∣ ∣ || ∣∣为拼接算子。
注意每个三维张量是由每个元路径 δ δ δ生成的,因此三维张量数目跟元路径数目相同。
2.3 压缩:
最后再在 H δ t \mathbb{H}^t_{\delta} Hδt上进行压缩操作,如图中右侧绿色部分所示。即沿特征维数方向对各层进行一维卷积运算,将三维张量压缩为二维张量 Z t Z^t Zt,计算公式为:
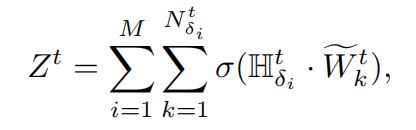
其中:
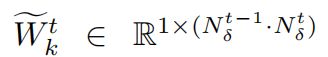
是第 k k k层的一维卷积, N δ i t N^t_{\delta_i} Nδit是在 t t t 时刻元路径 δ \delta δ 上的顶点数, ∣ M ∣ |M| ∣M∣是元路径的数目, σ \sigma σ是 s i g m o i d sigmoid sigmoid激活函数。
同时为了区分不同特征表示的权重,作者还在 Z t Z^t Zt上加一个注意分量,计算出相应的系数矩阵为:

其中 W ^ ∈ R d a \hat{W}\in\mathbb{R}^{d_a} W^∈Rda和 V ^ ∈ R d a × d \hat{V}\in\mathbb{R}^{d_a×d} V^∈Rda×d是参数矩阵,那么带有权重的输出就表示为:

为了避免高昂的计算成本和梯度消失问题,自然的选择是采用ResNet结构。因此,作者将原始特征矩阵加到模型输出 Z ^ T \hat{Z}^T Z^T上,有:
3. 伪代码:
社区检测:
为了将该模型用于社区检测,作者定义了一个类似于[Chen et al., 2019]的社区检测损失函数。在不损失一般性的前提下,本文考虑了非重叠社区检测问题。
根据[Chen et al., 2019],对于社区检测,节点标签应满足排列等方差性质,因此损失函数应根据节点标签的排列来设计。因此作者使用 s o f t m a x ( ⋅ ) softmax(·) softmax(⋅)函数,用于输出特征表示 Z t \mathbb{Z}^t Zt。假设 c ^ i \hat{c}_i c^i为顶点 i i i的预测社会标签, c i c_i ci表示顶点的真实社会标签, S C S_C SC表示排列,那么就可以给出该模型的损失函数:

其中 π \pi π是 S C S_C SC中的一组排列。
假设 Φ : X → C \Phi:X\rightarrow C Φ:X→C 是从 X X X 到真实标签 C C C的真实映射,并且 Ω : X → C ^ \Omega:X\rightarrow \hat{C} Ω:X→C^ 是从 X X X 到预测标签 C ^ \hat{C} C^ 的映射,那么就可以将损失函数改写为: