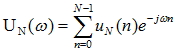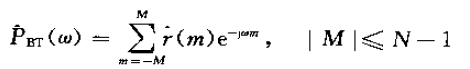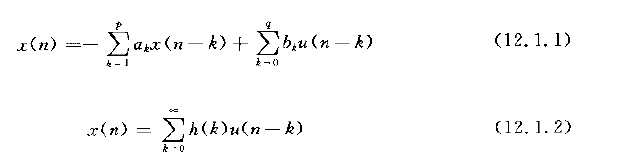matlab非参数功率普估计,【数字信号处理】--功率谱估计
文章目录
什么是功率谱估计?
经典谱估计法
周期图法-直接法
平均周期图法-Bartlett法
修正的平均周期图法-Welch法
间接法--BT法--自相关法
现代谱估计方法
基于参数建模的功率谱估计
AR模型-自回归模型
MA模型--移动平均模型
ARMA模型--自回归-移动平均模型
基于非参数建模的功率谱估计
评价功率谱的标准
参考资料
什么是功率谱估计?
谱估计在现代信号处理中是一个很重要的课题,功率谱反映了信号的功率在频域随频率w的分布,功率谱估计可以分为经典谱估计方法与现代谱估计方法。
简单说功率谱估计法是通过利用已经获得的N个数据点,来得到一个"非精确"的功率谱对真实随机信号的功率谱进行估计。
任意一个周期信号f(t),其傅里叶变换得到的频谱中将会包含一个直流分量,一个基频成分w0,以及相应的谐波成分。将这些信号分量相加就可以得到原始的时间信号f(t)。
信号分为确定信号和随机信号,而确定信号又分为能量信号和功率信号。根据狄里赫利条件,能量信号可以直接进行傅里叶变换,得到频谱的幅度再平方即为能量谱(或称能量谱密度)。而功率信号不行。
功率谱密度的求法:
如果你测到的信号是一个确定性信号,你就可以直接做FFT,然后平方,再除以你用的点数就得到其功率谱密度;如果你测到的信号是一个随机信号,就需要先求自相关函数,然后对自相关求FFT得到其功率谱密度曲线
确定信号是用FFT求频谱,先FFT,再幅值平方/N
随机信号是用PSD、pwelch求功率谱,先求自相关,再FFT
功率谱估计方法的分类
经典谱估计法
经典谱估计中分为直接法与间接法。最简单的就是周期图法。
周期图法-直接法
我们已知N个离散的数据点,对这些数据点进行傅里叶变换,得到式
再对式取模的平方,除以N,即得到一个"非精确"的谱,如式示,这就是周期图法的原理。
周期图法的特点:周期图法得到的功率谱随着数据点数N的增大,分辨率变大、方差变也大。
在matlab中,周期图法可以川函数periodogram实现。
平均周期图法-Bartlett法
数据分段,减小方差
数据窗口加窗-矩形窗
将N个观测样本数据点分为L段,每段数据长度为M,分别对每段数据求周期图功率谱估计,然后求平均值,这种方法称平均周期图法。平均周期图法将原来的方差变为原来的1/L,L为分段数。
L=1时,平均周期图法退化为周期图法。
特点:平均周期图法得到的功率谱随着分段数L变大,方差变小,但分辨率变小。
当观测样本序列数据个数N固定时,要降低方差需要增加分段数L。当N不大时分段长度M取值较小,则功率谱分辨率降低到较低的水平。若分段数L固定时,增加分辨率需要分段长度M,则需要采集到更长的检测数据序列。实际中恰恰是检测样本序列长度不足。
在matlab中,平均周期图法可以用函数psd、pwelch实现。
修正的平均周期图法-Welch法
数据分段并重叠
数据窗口加不同的窗函数
对现有数据长度N,如果能获得更多的段数分割,将会得到更小的方差。允许数据段间有重叠部分,来得到更多的段数。对段间重叠长度的选取,最简单是取为段长度M的一半。可知更多的段数可以进一步降低方差。
数据截断的过程中相当于数据加矩形窗,矩形窗幅度较大的旁瓣会造成"频谱泄漏"。关于“频谱泄漏”如果有不明白,请看这篇文章。我们分段时采取的窗函数更为多样(三角窗,海明窗等), 以减小截断数据(加矩形窗)窗函数带来的影响。
矩形窗的分辨率最高,但是方差也最大,这是由于矩形窗频谱主瓣最窄,分辨率因此最高,旁瓣也高,导致频谱泄漏最严重,方差最大。
总结:周期图法获得的功率谱随着样本点数越多,分辨率越大、方差越大;平均周期图法以牺牲分辨率来进一步改善方差;修正的平均周期图法允许段的重叠来进一步增大分段数、或者分段数相同,每段样本点数变多。无论是哪种方法都没有彻底结局方差与分辨率之间的矛盾。
间接法–BT法–自相关法
维纳辛钦定理指出,随机信号的相关函数与它的功率谱是一对傅里叶变换对。BT法就是基于这个原理。先由观测数据估计出自相关函数,然后求自相关函数的傅立叶变换,以此变换作为对功率谱的估计,也称为间接法。BT法要求信号长度N以外的信号为零,这也造成BT法的局限性。
通过逆变换求得自相关函数。
M随着N的增大而增大时,分辨率提高,方差变大。BT法仍然没有解决分辨率与方差之间的矛盾,但是BT法得到的功率谱当N为无穷大时,方差会趋向于零,即为一致估计
总结:可以看出,无论是周期图法及其改进算法还是BT法都没有从根本上解决分辨率与方差的矛盾。经典功率谱估计是利用傅里叶变换估计功率谱,而我们之前分析随机信号不满足傅里叶变换的条件,所以经典功率谱估计方法不得不从无限长数据点截取有限长数据点,加入限制条件(周期图法实际上假定N点外数据周期重复、BT法假定N点外数据为零)来"强制"作傅里叶变换,这也是造成它局限性的原因
现代谱估计方法
现代谱的分辨率较高。这是由于在时域的开窗,使得在频域发生“频谱泄漏”,即功率谱的主瓣能量泄漏到旁瓣中,导致弱信号的主瓣被强信号的旁瓣所湮没,造成谱的模糊。
现代谱估计主要针对经典谱估计分辨率低和方差性不好提出的,可以极大的提高估计的分辨率和平滑性。可以分为参数模型谱估计和非参数模型谱估计。
参数模型谱估计有AR模型,MA模型,ARMA模型等;非参数模型谱估计有最小方差法和MUSIC法等。由于涉及的问题太多,这里不再详述,可以参考有关资料。
在MATLAB中.主要有基于AR模型的功率谱估计pyulear函数、pburg函数、pcov函数、pmov函数和pmem函数R,,。在下面的仿真实验中,发现pyulear函数的运算速度在它们当中最快,分辨力最好,故以pyulear函数为例进行分析。
基于参数建模的功率谱估计
无论对于一个确定性信号还是随机信号,其输入、输出关系总是如下:
AR模型-自回归模型
易于反映功率谱中的峰值。
建立AR模型的参数ak和x(n)的自相关函数的关系,即正则方程。
一个p阶的AR模型等效于一个p阶的线性预测器。根据已知的自相关函数rx(m),求解Yule-Walker方程得到模型的p+1个参数a(1)、、、a§和方差,实现功率谱的估计。
AR模型是在最小平方意义上对数据的拟合。
Burg提出最大熵谱估计
AR模型阶次的选择,根据模型的最小预测误差功率进行选择。
MA模型–移动平均模型
易于反映功率谱中的谷值。
ARMA模型–自回归-移动平均模型
易于反映功率谱中的峰值和谷值。
基于非参数建模的功率谱估计
该方法主要墓于矩阵特征分解的功率谱估计,它将相关矩阵的特征向量空间分解为信号子空间和噪声子空间.由此衍生出特征向量与MUSIC
算法的信号功率i替估计。其中特征向量谱估计与MUSIC算法谱估计都是基于噪声子空间的功率谱估计。
在MATLAB中,有可以利用函数pmusic来实现MUSIC算法的功率谱估计;也有可以利用函数peig来实现特征向量的功率诺估计
评价功率谱的标准
给出两个影响最大的标准:分辨率和方差。
分辨率即功率谱上能够区分的最小相邻频率成分,分辨率越高,我们观察信号的频率成分越清晰;方差大小则反映到功率谱波动性的大小,如果方差太大,功率谱波动性大,则很容易造成有用的频率成分被噪声淹没。所以,我们希望得到的这个"非精确"的功率谱,分辨率越高越好,方差越小越好。
参考资料
经典功率谱估计及Matlab仿真 https://www.cnblogs.com/jacklu/p/5140913.html
MATLAB中几种功率谱估计函数的比较分析与选择 https://wenku.baidu.com/view/08fb8cf627fff705cc1755270722192e44365851.html?rec_flag=default&sxts=1590983291605
随机信号傅里叶变换和功率谱密度图给出的信息有什么不同 https://www.ilovematlab.cn/thread-291253-1-1.html