机器学习初探：（五）逻辑回归之多分类

（五）逻辑回归 - 多分类

​ 图片出处

在 机器学习初探：（四）逻辑回归之二分类一文中，我们介绍了逻辑回归算法（Logistic regression）。逻辑回归属于 有监督学习中的一种 分类方法，其进行分类的主要思想是：根据现有数据 对决策边界线建立回归公式，以此进行分类。相比于线性回归，逻辑回归通过 Sigmoid 函数将线性回归模型的预测值（ ${\Theta }^{T}X$）映射至 0 和 1 之间， 其输出表示样本属于某一类别的概率。

回顾： 逻辑回归模型的基本形式：$h_{\Theta }(x)=\frac{1}{1+e^{-{\Theta }^{T}X}}$

在上一篇文章中，我们主要讨论的是如何使用逻辑回归训练一个二分类任务，即其输出标记仅有两种，比如是否被录取、邮件是否为垃圾邮件等。然而，现实世界的很多分类任务中具有两个以上分类类别，比如天气状况的预测，即存在晴天（$y=1$）、多云（$y=2$）、下雨（$y=3$）、下雪（$y=4$）等至少四类情况。那么如何将前一篇文章中我们建立的二分类逻辑回归模型扩展至多分类的情况呢？

在正式开始介绍之前，我们还是以一个例子来引入。如今，手写数字的自动识别得到了广泛的应用——比如，识别邮政编码、确认银行支票上的金额… 在此篇中，我们将尝试构建一个逻辑回归多分类模型（One-vs-all logistic regression），来实现手写数字（由 0 至 9）的自动识别¹…

图1 手写体识别

逻辑回归多分类（One-vs-all logistic regression）

上面的例子是一个典型的多分类任务，存在0至9共10个类别。那么如何将前一篇文章中我们建立的二分类逻辑回归模型扩展至多分类的情况呢？

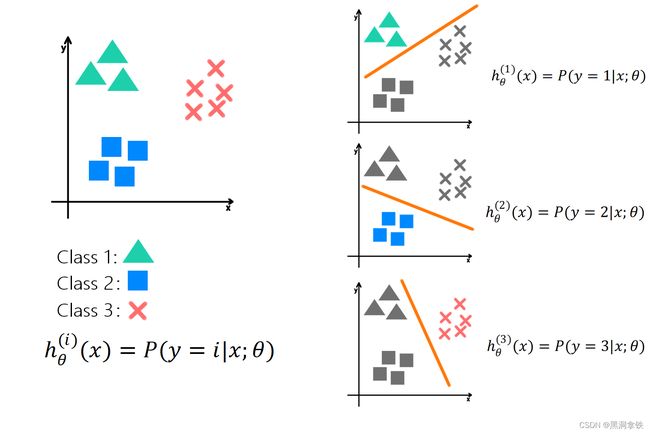
一种直观的想法便是，对于每个类别都单独训练一个二分类逻辑回归模型，该模型解决的是判断样本是否属于这一类的问题。比如，下图2中共存在三角（Class 1）、方块（Class 2）、叉叉（Class 3）三个类别，实现上述三个类别的划分共需训练 3 个二分类逻辑回归模型：其中，$h_{\theta }^{(1)}(x)$ 用于区分三角和非三角；$h_{\theta }^{(2)}(x)$ 用来区分方块和非方块；$h_{\theta }^{(3)}(x)$ 用于区分叉叉和非叉叉。这便是 One-vs-all 分类的基本思想。

图2 One-vs-all分类的基本思想

接下来，在做预测的时候，对于每个新的输入，使用训练出的分类器分别计算“样本属于每个类别的概率”，进而，选择概率值最高的那个类别作为该样本的预测类别。

One-vs-all分类基本思想：

• 对于每个类别 $i$, 单独训练一个二分类逻辑回归模型 $h_{\theta }^{(i)}(x)$ 用于预测样本属于类别 $i$ ($y=i$) 的概率
• 对于新的输入 $x$, 选择最大化 $h_{\theta }^{(i)}(x)$ 的类别 $i$ 作为 $x$ 的预测类别

逻辑回归的一般流程

训练 $h_{\theta }^{(i)}(x)$ 的方法与前文机器学习初探：（四）逻辑回归之二分类 的方法一致，即：1）基于输入数据 $x$ 以及初始化参数 $\theta$ 计算损失函数 $J$；2）使用梯度下降算法计算 $\frac{\delta J}{\delta \theta }$； 3）基于对调整步长的设定，使用计算出来的 $\frac{\delta J}{\delta \theta }$ 调整 $\theta$ 值。至此，完成算法的一轮迭代（如下图3²所示）。

图3 使用梯度下降算法训练逻辑回归模型的一般流程

需说明的是，前述文章我们介绍的梯度下降算法均为 Batch gradient descent, 即在每轮迭代（对参数进行一次调整）中，即使用所有的训练样本数据来计算 $J(\theta )$ 和 $\frac{\delta J}{\delta \theta }$，并调整参数的。

对于损失函数、梯度下降算法的实现细节，与机器学习初探：（四）逻辑回归之二分类一文中一致，在此不再赘述。

逻辑回归多分类实例

有了上述的知识储备，我们来具体看一下，如何通过逻辑回归多分类训练一个手写数字的识别模型。

让机器识别图片中的数字，解决这个问题的关键点在于图片的数据形式化表示。一个直觉的思维是，我如果能够找到图像中每个物体或状态的数字规律，就可以实现对图像的识别了？

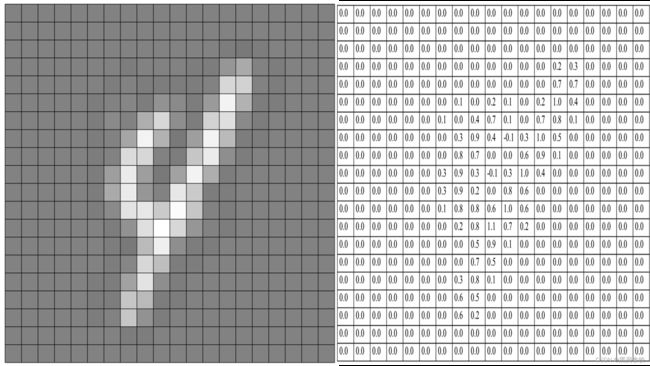
以手写数字”4“的图片为例，我们眼中看到的数字如下图 4 左所示，那么计算机“看到”的图像是什么样呢？我们知道一幅图像在计算机中是采用数字形式表示的。比如一张黑白图像，计算机中一般采用0-255的数字来表示每个像素点的亮度。如下图 4 中所示，数字“4”的灰度图像由 20 $\times$ 20 的像素点构成，其中，每个像素点在计算机中被表示为一个浮点数字，表示图片中对应位置的灰度强度，即如下图 4 右侧数字网格所示。

图4 计算机中的图像表示

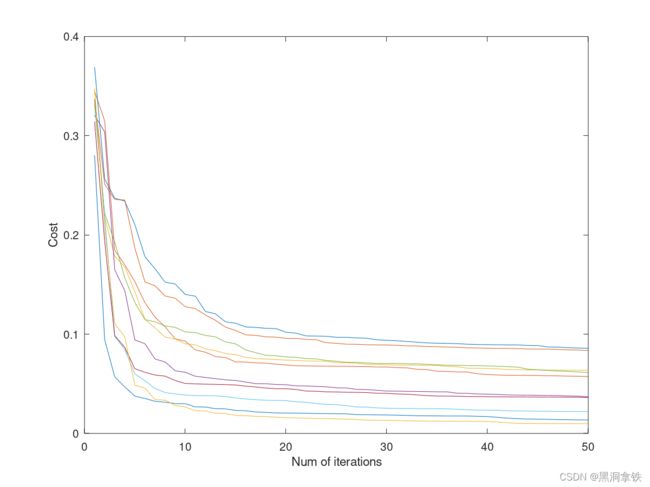
在训练模型时，20 $\times$ 20 的像素网格数据被展开成 400 $\times$ 1 维的向量，相当于一个具有 400 维特征的输入样本，其对应的标签为 $y=4$。在我们的数据集中，共有 5000 个类似的训练样本，机器就可以通过分析输入的数字规律，实现对手写数字的识别了。对于本篇中的手写数字识别问题，需要训练 10 个不同的二分类逻辑回归模型。下图 5 即展示了 10 个分类器的训练过程（其中，横轴为迭代次数、纵轴为损失函数值，不同颜色的线对应 10 个分类器）。可以看到，在迭代到 50 次时，损失函数值基本维持在一定水平，也即模型训练基本稳定。

图5 逻辑回归多分类训练过程

模型训练好之后，我们可以统计一下，若使用训练好的模型进行预测的话，它的效果如何。经统计，我们训练的逻辑回归多分类模型在训练数据集上的预测准确度为 94.9%， 即训练数据中约有 94.9% 的手写数字图片可以被正确识别。

这似乎是个还算不错的结果，但需要注意的是，这仅是在训练数据集上的效果，如果是模型从未见过的数据呢，效果也会这么好吗？这属于模型泛化的问题，我们将在后续的系列文章中进行介绍。此外，上述结果是否还存在进一步提升的空间呢？在后续的文章中，我们将介绍另一类有监督学习算法——神经网络，届时我们将对这个问题进行解答。

小结

在此篇文章中，我们介绍了逻辑回归多分类方法。通过对每个类别单独训练一个二分类逻辑回归模型，来解决多分类的学习任务。

此外，我们回顾了使用梯度下降算法求解逻辑回归模型的一般流程，即：初始化参数值、计算损失函数、计算损失函数关于参数的偏导数、参数调整等过程。

最后，我们首次接触了图像识别问题，了解了计算机中的图像表示方式，并使用逻辑回归多分类训练了一个手写数字识别的模型。

参考资料

---

1. 数据来自吴恩达机器学习课程. ↩︎

2. 吴恩达. Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization. ↩︎