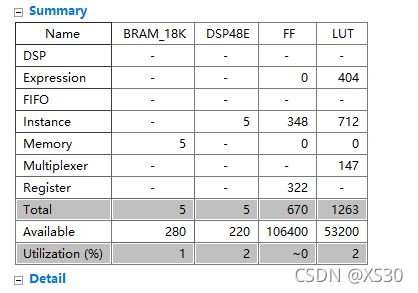
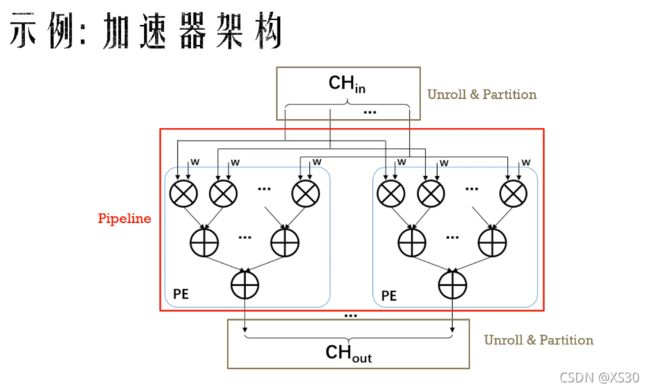
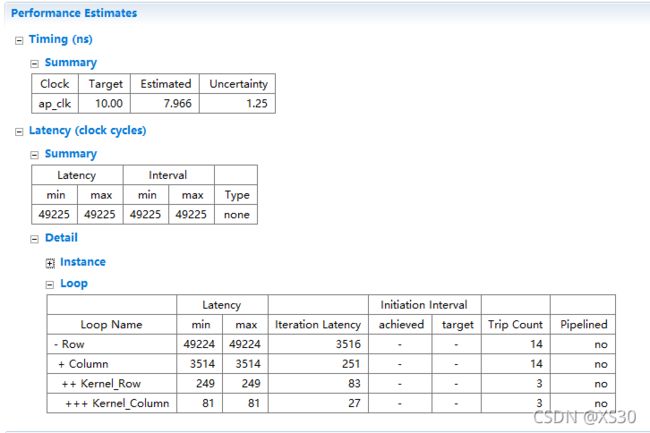
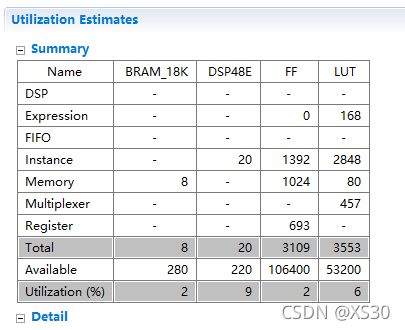
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
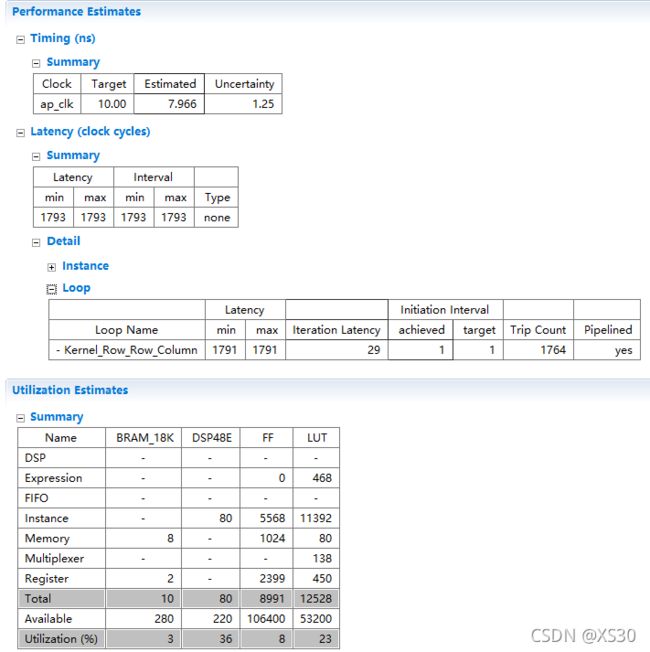
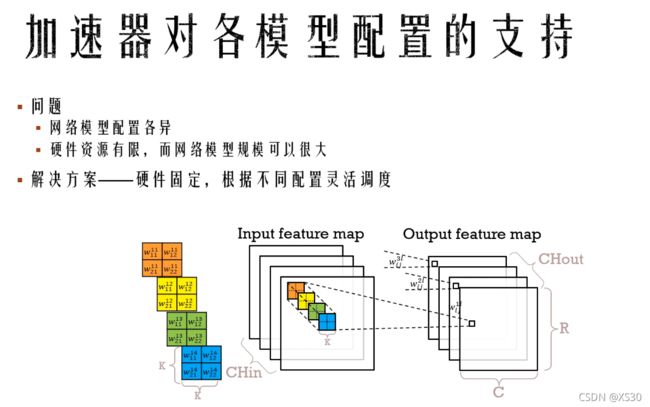
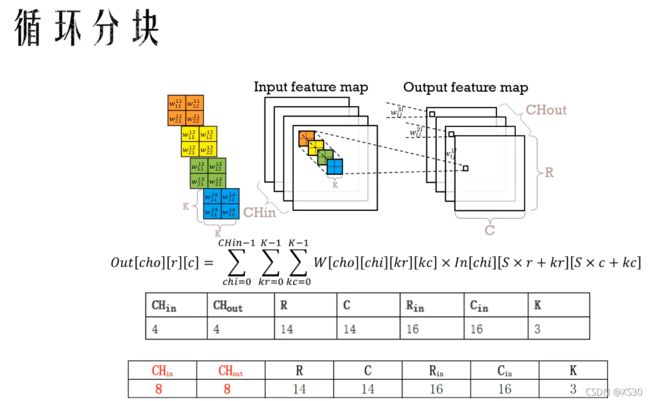
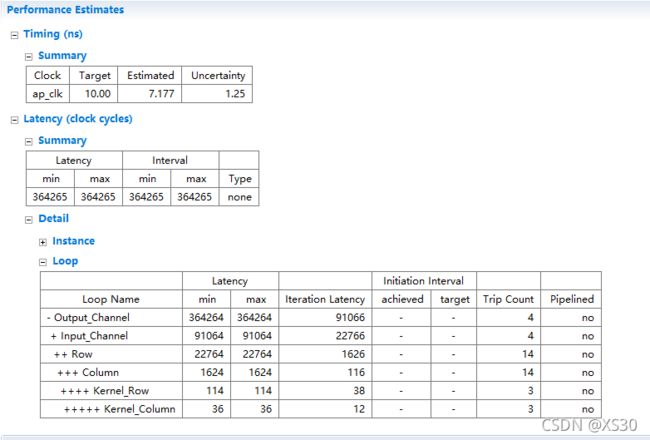
- (179)时序收敛--->(29)时序收敛二九
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛二九(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- (180)时序收敛--->(30)时序收敛三十
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三十(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- (158)时序收敛--->(08)时序收敛八
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛八(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (159)时序收敛--->(09)时序收敛九
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛九(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (160)时序收敛--->(10)时序收敛十
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛十(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (153)时序收敛--->(03)时序收敛三
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)F
- (121)DAC接口--->(006)基于FPGA实现DAC8811接口
FPGA系统设计指南针
FPGA接口开发(项目实战)fpga开发FPGAIC
1目录(a)FPGA简介(b)IC简介(c)Verilog简介(d)基于FPGA实现DAC8811接口(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电
- FPGA复位专题---(3)上电复位?
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发
(3)上电复位?1目录(a)FPGA简介(b)Verilog简介(c)复位简介(d)上电复位?(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限
- (182)时序收敛--->(32)时序收敛三二
FPGA系统设计指南针
FPGA系统设计(内训)fpga开发时序收敛
1目录(a)FPGA简介(b)Verilog简介(c)时钟简介(d)时序收敛三二(e)结束1FPGA简介(a)FPGA(FieldProgrammableGateArray)是在PAL(可编程阵列逻辑)、GAL(通用阵列逻辑)等可编程器件的基础上进一步发展的产物。它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器件门电路数有限的缺点。(b)
- 使用FPGA接收MIPI CSI RX信号并进行去抖动、RGB转YUV处理:FX3014 USB3.0 UVC传输与帧率控制源代码,FPGA实现MIPI CSI RX接收,去Debayer, RGB转
kVfINoSzdrt
fpga开发程序人生
fpgamipicsirx接收去debayer,rgb转yuv,fx3014usb3.0uvc传输与帧率控制源代码,具体架构看图,除dphy物理层外,mipi均为源码sensorimx219mipi源码mipi4lanecsirxraw10fpgamachXO3lf-690usb3.0fx301432bityuvdatawithframesync测试模式3280*246415fps1920*108
- FPGA_mipi
哈呀_fpga
fpga开发逻辑高速接口系统架构高速传输
1mipi接口mipi(移动行业处理器接口,是为高速数据传输量身定做的,旨在解决日益增长的高清图像(视频)传输的高带宽要求与传统接口低速率之间的矛盾。采用差分信号传输,在设计时需要按照差分设计的一般规则进行严格的设计。mipi协议提出之际,主要有2个应用,csi(摄像头串行接口),旨在为高清摄像头和应用处理器之间提供一个高速串行接口,和dsi(显示串行接口),旨在为应用处理器和显示设备之间提供一个
- PCIe进阶之TL:Common Packet Header Fields & TLPs with Data Payloads Rules
芯芯之火,可以燎原
PCIe进阶PCIe进阶硬件工程信息与通信
1TransactionLayerProtocol-PacketDefinitionTLP有四种事务类型:Memory、I/O、Configuration和Messages,两种地址格式:32bit和64bit。构成TLP时,所有标记为Reserved的字段(有时缩写为R)都必须全为0。接收者Rx必须忽略此字段中的值,PCIeSwitch必须对其进行原封不动的转发。请注意,对于某些字段,既有指定值
- Xilinx 7系列FPGA架构之器件配置(二)
FPGA技术实战
FPGA器件架构XinxFPGA硬件设计fpga开发
引言:本文我们介绍下7系列FPGA的配置接口,在进行硬件电路图设计时,这也是我们非常关心的内容,本文主要介绍配置模式的选择、配置管脚定义以及如何选择CFGBVS管脚电压及Bank14/15电压。1.概述Xilinx®7系列设备有五个配置接口。每个配置接口对应一个或多个配置模式和总线宽度,如表1所示。有关接口详细的时序信息,可以参阅相应的7系列FPGA数据手册。配置时序主要与FPGA配置时钟管脚CC
- Xilinx 7系列FPGA架构之器件配置(一)
FPGA技术实战
FPGA器件架构XinxFPGA硬件设计fpga开发
引言:本系列博文描述7系列FPGA配置的技术参考。作为开篇,简要概述了7系列FPGA的配置方法和功能。随后的博文将对每种配置方法和功能进行更详细的描述。本文描述的配置方法和功能适用于所有7系列家族器件,只有少数例外。1.概述Xilinx®7系列FPGA通过将特定于应用程序的配置数据(位流)加载到内存中进行配置。7系列FPGA可以主动从外部非易失性存储设备加载,也可以通过外部智能源(如微处理器、DS
- FPGA器件在线配置方法概述
fpga和matlab
FPGA其他fpga开发FPGA在线配置
目录1.配置电路结构和原理2.ICR控制电路软件3.几种常见的FPGA在线配置方法3.1动态部分重配置(PartialReconfiguration,PR)3.2在系统编程(In-SystemProgramming,ISP)3.3多比特流配置(Multi-BitstreamConfiguration)3.4远程更新与配置3.5使用OpenCL或HLS工具FPGA(Field-Programmabl
- quartus频率计 时钟设置_FPGA021 基于QuartusⅡ数字频率计的设计与仿真
weixin_39876739
quartus频率计时钟设置
摘要随着科技电子领域的发展,可编程逻辑器件,例如CPLD和FPGA的在设计中得到了广泛的应用和普及,FPGA/CPLD的发展使数字设计更加的灵活。这些芯片可以通过软件编程的方式对内部结构进行重构,使它达到相应的功能。这种设计思想改变了传统的数字系统设计理念,促进了EDA技术的迅速发展。数字频率计是一种基本的测量仪器。它被广泛应用与航天、电子、测控等领域。采用等精度频率测量方法具有测量精度保持恒定,
- quartus pin 分配(三)
落雨无风
IC设计fpgafpga开发
quartuspin分配如有需要,可查看quartusUI界面sdc配置(二)上次文章中,说了自己写sdc需要配置的分类点,这次将介绍管脚分配。已打开Quartus软件,导入设计,写好约束下一步,在Quartus软件的菜单栏打开Assignments中的二级菜单PinPlanner打开改界面即可看到选中的fpga型号,管脚图,封装类型等信息。在打开的界面中,大致可分为上下两个部分。上半部分,可分为
- 《Android进阶之光》— Android 书籍
王睿丶
Android永无止境《Android进阶之光》Android书籍Androidphoenix移动开发
文章目录第1章Android新特性1第2章MaterialDesign48第3章View体系与自定义View87第4章多线程编程165第5章网络编程与网络框架204第6章设计模式271第7章事件总线308第8章函数响应式编程333第9章注解与依赖注入框架382第10章应用架构设计422第11章系统架构与MediaPlayer框架460出版年:2017-7简介:《Android进阶之光》是一本And
- PCIe进阶之Gen3 Physical Layer Transmit Logic(二)
芯芯之火,可以燎原
PCIe进阶硬件工程信息与通信
1文章概述本文是接着上面一篇文章《Gen3PhysicalLayerTransmitLogic(一)》继续对Gen3PhysicalLayerTransmitLogic做进一步的解析,具体包含ByteStriping和Scrambling以及Serializer。1.1ByteStripingGen3x1OrderedSetConstruction如下所示:OrderedSetBlock由一个Sy
- PCIe进阶之Gen3 Physical Layer Receive Logic(一)
芯芯之火,可以燎原
PCIe进阶硬件工程信息与通信
1文章概述本篇文章是接着前面两篇文章进一步研究Gen3PhysicalLayerReceiveLogic的实现,具体包含DifferentialReceiver,CDR(ClockandDataRecovery)和ReceiverClockCompensationLogic三个部分的介绍和解析。1.1DifferentialReceiverGen3的DifferentialReceiver逻辑和之
- ModuleNotFoundError: No module named ‘timm.layers‘
忽略不计,
BUGpythonYOLO目标检测人工智能深度学习
解决方式:把fromtimm.layersimportDropPath这个修改为fromtimm.models.layersimportDropPath即可。
- FPGA随记——赛灵思OOC功能
一口一口吃成大V
FPGA随记fpga开发
在这里,我们简要介绍一下Vivado的OOC(Out-of-Context)综合的概念。对于顶层设计,Vivado使用自顶向下的全局(Global)综合方式,将顶层之下的所有逻辑模块都进行综合,但是设置为OOC方式的模块除外,它们独立于顶层设计而单独综合。通常,在整个设计周期中,顶层设计会被多次修改并综合。但有些子模块在创建完毕之后不会因为顶层设计的修改而被修改,如IP,它们被设置为OOC综合方式
- 【Unity基础】如何选择脚本编译方式Mono和IL2CPP?
tealcwu
Unity基础unity游戏引擎
Edit->ProjectSettings->Player在Unity中,ScriptingBackend决定了项目的脚本编译方式,即如何将C#代码转换为可执行代码。Unity提供了两种主要的ScriptingBackend选项:Mono和IL2CPP。它们之间的区别影响了项目的性能、平台支持、编译时间和调试体验。以下是两者的详细对比:1.Mono简介:Mono是Unity最早使用的脚本后端,基于
- 多层建筑能源参数化模型和城市冠层模型的区别
WW、forever
WRF模型原理及应用城市模拟
多层建筑能源参数化(Multi-layerBuildingEnergyParameterization,BEP)模型和城市冠层模型(UrbanCanopyModel,UCM)都是用于模拟城市环境中能量交换和微气候的数值模型,但它们的侧重点和应用场景有所不同。以下是两者的主要区别:1.目标和应用场景BEP模型:目标:主要用于模拟多层建筑群的能量交换过程,特别是建筑内部和外部的热量传输、建筑能耗以及建
- 如何设计实现完成一个FPGA项目
芯作者
D1:verilog设计D1:VHDL设计fpga开发
设计并完成一个FPGA项目是一个复杂但非常有价值的工程任务。以下是一个详细的步骤指南,帮助你从零开始完成一个FPGA项目。1.项目定义与需求分析确定项目目标:明确项目要实现的功能和性能指标。需求分析:列出所有功能需求、性能需求、接口需求等。可行性分析:评估技术可行性、成本和时间预算。2.硬件选择FPGA芯片选择:根据项目需求选择合适的FPGA芯片(如Xilinx、Intel/Altera、Latt
- docker Pulling fs layer 含义
潇锐killer
eurekajavaspringcloud
在使用Docker时,当你执行dockerpull命令来获取一个新的镜像,控制台输出中可能会出现"Pullingfslayer"的信息。这是Docker拉取镜像过程中的一个步骤,下面是对这一过程的解释:Docker镜像是由一系列的层(layers)组成的。每个层代表了镜像构建过程中的一个步骤,比如安装一个软件包或复制一些文件。这种层式结构使得Docker镜像既轻便又高效,因为它允许多个镜像共享相同
- ExoPlayer简单使用
csdn_zxw
安卓视频播放android
ExoPlayerLibrary概述ExoPlayer是运行在YouTubeappAndroid版本上的视频播放器ExoPlayer是构建在Android低水平媒体API之上的一个应用层媒体播放器。和Android内置的媒体播放器相比,ExoPlayer有许多优点。ExoPlayer支持内置的媒体播放器支持的所有格式外加自适应格式DASH和SmoothStreaming。ExoPlayer可以被高
- ExoPlayer架构详解与源码分析(17)——TrackSelector
山雨楼
ExoPlayer架构android音视频ExoPlayerMedia3源码
系列文章目录ExoPlayer架构详解与源码分析(1)——前言ExoPlayer架构详解与源码分析(2)——PlayerExoPlayer架构详解与源码分析(3)——TimelineExoPlayer架构详解与源码分析(4)——整体架构ExoPlayer架构详解与源码分析(5)——MediaSourceExoPlayer架构详解与源码分析(6)——MediaPeriodExoPlayer架构详解与
- ExoPlayer架构详解与源码分析(12)——Cache
山雨楼
ExoPlayer架构android音视频ExoPlayerMedia3源码
系列文章目录ExoPlayer架构详解与源码分析(1)——前言ExoPlayer架构详解与源码分析(2)——PlayerExoPlayer架构详解与源码分析(3)——TimelineExoPlayer架构详解与源码分析(4)——整体架构ExoPlayer架构详解与源码分析(5)——MediaSourceExoPlayer架构详解与源码分析(6)——MediaPeriodExoPlayer架构详解与
- scala的option和some
矮蛋蛋
编程scala
原文地址:
http://blog.sina.com.cn/s/blog_68af3f090100qkt8.html
对于学习 Scala 的 Java™ 开发人员来说,对象是一个比较自然、简单的入口点。在 本系列 前几期文章中,我介绍了 Scala 中一些面向对象的编程方法,这些方法实际上与 Java 编程的区别不是很大。我还向您展示了 Scala 如何重新应用传统的面向对象概念,找到其缺点
- NullPointerException
Cb123456
androidBaseAdapter
java.lang.NullPointerException: Attempt to invoke virtual method 'int android.view.View.getImportantForAccessibility()' on a null object reference
出现以上异常.然后就在baidu上
- PHP使用文件和目录
天子之骄
php文件和目录读取和写入php验证文件php锁定文件
PHP使用文件和目录
1.使用include()包含文件
(1):使用include()从一个被包含文档返回一个值
(2):在控制结构中使用include()
include_once()函数需要一个包含文件的路径,此外,第一次调用它的情况和include()一样,如果在脚本执行中再次对同一个文件调用,那么这个文件不会再次包含。
在php.ini文件中设置
- SQL SELECT DISTINCT 语句
何必如此
sql
SELECT DISTINCT 语句用于返回唯一不同的值。
SQL SELECT DISTINCT 语句
在表中,一个列可能会包含多个重复值,有时您也许希望仅仅列出不同(distinct)的值。
DISTINCT 关键词用于返回唯一不同的值。
SQL SELECT DISTINCT 语法
SELECT DISTINCT column_name,column_name
F
- java冒泡排序
3213213333332132
java冒泡排序
package com.algorithm;
/**
* @Description 冒泡
* @author FuJianyong
* 2015-1-22上午09:58:39
*/
public class MaoPao {
public static void main(String[] args) {
int[] mao = {17,50,26,18,9,10
- struts2.18 +json,struts2-json-plugin-2.1.8.1.jar配置及问题!
7454103
DAOspringAjaxjsonqq
struts2.18 出来有段时间了! (貌似是 稳定版)
闲时研究下下! 貌似 sruts2 搭配 json 做 ajax 很吃香!
实践了下下! 不当之处请绕过! 呵呵
网上一大堆 struts2+json 不过大多的json 插件 都是 jsonplugin.34.jar
strut
- struts2 数据标签说明
darkranger
jspbeanstrutsservletScheme
数据标签主要用于提供各种数据访问相关的功能,包括显示一个Action里的属性,以及生成国际化输出等功能
数据标签主要包括:
action :该标签用于在JSP页面中直接调用一个Action,通过指定executeResult参数,还可将该Action的处理结果包含到本页面来。
bean :该标签用于创建一个javabean实例。如果指定了id属性,则可以将创建的javabean实例放入Sta
- 链表.简单的链表节点构建
aijuans
编程技巧
/*编程环境WIN-TC*/ #include "stdio.h" #include "conio.h"
#define NODE(name, key_word, help) \ Node name[1]={{NULL, NULL, NULL, key_word, help}}
typedef struct node { &nbs
- tomcat下jndi的三种配置方式
avords
tomcat
jndi(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。命名服务将名称和对象联系起来,使得我们可以用名称
访问对象。目录服务是一种命名服务,在这种服务里,对象不但有名称,还有属性。
tomcat配置
- 关于敏捷的一些想法
houxinyou
敏捷
从网上看到这样一句话:“敏捷开发的最重要目标就是:满足用户多变的需求,说白了就是最大程度的让客户满意。”
感觉表达的不太清楚。
感觉容易被人误解的地方主要在“用户多变的需求”上。
第一种多变,实际上就是没有从根本上了解了用户的需求。用户的需求实际是稳定的,只是比较多,也比较混乱,用户一般只能了解自己的那一小部分,所以没有用户能清楚的表达出整体需求。而由于各种条件的,用户表达自己那一部分时也有
- 富养还是穷养,决定孩子的一生
bijian1013
教育人生
是什么决定孩子未来物质能否丰盛?为什么说寒门很难出贵子,三代才能出贵族?真的是父母必须有钱,才能大概率保证孩子未来富有吗?-----作者:@李雪爱与自由
事实并非由物质决定,而是由心灵决定。一朋友富有而且修养气质很好,兄弟姐妹也都如此。她的童年时代,物质上大家都很贫乏,但妈妈总是保持生活中的美感,时不时给孩子们带回一些美好小玩意,从来不对孩子传递生活艰辛、金钱来之不易、要懂得珍惜
- oracle 日期时间格式转化
征客丶
oracle
oracle 系统时间有 SYSDATE 与 SYSTIMESTAMP;
SYSDATE:不支持毫秒,取的是系统时间;
SYSTIMESTAMP:支持毫秒,日期,时间是给时区转换的,秒和毫秒是取的系统的。
日期转字符窜:
一、不取毫秒:
TO_CHAR(SYSDATE, 'YYYY-MM-DD HH24:MI:SS')
简要说明,
YYYY 年
MM 月
- 【Scala六】分析Spark源代码总结的Scala语法四
bit1129
scala
1. apply语法
FileShuffleBlockManager中定义的类ShuffleFileGroup,定义:
private class ShuffleFileGroup(val shuffleId: Int, val fileId: Int, val files: Array[File]) {
...
def apply(bucketId
- Erlang中有意思的bug
bookjovi
erlang
代码中常有一些很搞笑的bug,如下面的一行代码被调用两次(Erlang beam)
commit f667e4a47b07b07ed035073b94d699ff5fe0ba9b
Author: Jovi Zhang <
[email protected]>
Date: Fri Dec 2 16:19:22 2011 +0100
erts:
- 移位打印10进制数转16进制-2008-08-18
ljy325
java基础
/**
* Description 移位打印10进制的16进制形式
* Creation Date 15-08-2008 9:00
* @author 卢俊宇
* @version 1.0
*
*/
public class PrintHex {
// 备选字符
static final char di
- 读《研磨设计模式》-代码笔记-组合模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
abstract class Component {
public abstract void printStruct(Str
- 利用cmd命令将.class文件打包成jar
chenyu19891124
cmdjar
cmd命令打jar是如下实现:
在运行里输入cmd,利用cmd命令进入到本地的工作盘符。(如我的是D盘下的文件有此路径 D:\workspace\prpall\WEB-INF\classes)
现在是想把D:\workspace\prpall\WEB-INF\classes路径下所有的文件打包成prpall.jar。然后继续如下操作:
cd D: 回车
cd workspace/prpal
- [原创]JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
comsci
eclipse设计模式算法工作swing
JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
&nb
- SecureCRT右键粘贴的设置
daizj
secureCRT右键粘贴
一般都习惯鼠标右键自动粘贴的功能,对于SecureCRT6.7.5 ,这个功能也已经是默认配置了。
老版本的SecureCRT其实也有这个功能,只是不是默认设置,很多人不知道罢了。
菜单:
Options->Global Options ...->Terminal
右边有个Mouse的选项块。
Copy on Select
Paste on Right/Middle
- Linux 软链接和硬链接
dongwei_6688
linux
1.Linux链接概念Linux链接分两种,一种被称为硬链接(Hard Link),另一种被称为符号链接(Symbolic Link)。默认情况下,ln命令产生硬链接。
【硬连接】硬连接指通过索引节点来进行连接。在Linux的文件系统中,保存在磁盘分区中的文件不管是什么类型都给它分配一个编号,称为索引节点号(Inode Index)。在Linux中,多个文件名指向同一索引节点是存在的。一般这种连
- DIV底部自适应
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- Centos6.5使用yum安装mysql——快速上手必备
dcj3sjt126com
mysql
第1步、yum安装mysql
[root@stonex ~]# yum -y install mysql-server
安装结果:
Installed:
mysql-server.x86_64 0:5.1.73-3.el6_5 &nb
- 如何调试JDK源码
frank1234
jdk
相信各位小伙伴们跟我一样,想通过JDK源码来学习Java,比如collections包,java.util.concurrent包。
可惜的是sun提供的jdk并不能查看运行中的局部变量,需要重新编译一下rt.jar。
下面是编译jdk的具体步骤:
1.把C:\java\jdk1.6.0_26\sr
- Maximal Rectangle
hcx2013
max
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
public class Solution {
public int maximalRectangle(char[][] matrix)
- Spring MVC测试框架详解——服务端测试
jinnianshilongnian
spring mvc test
随着RESTful Web Service的流行,测试对外的Service是否满足期望也变的必要的。从Spring 3.2开始Spring了Spring Web测试框架,如果版本低于3.2,请使用spring-test-mvc项目(合并到spring3.2中了)。
Spring MVC测试框架提供了对服务器端和客户端(基于RestTemplate的客户端)提供了支持。
&nbs
- Linux64位操作系统(CentOS6.6)上如何编译hadoop2.4.0
liyong0802
hadoop
一、准备编译软件
1.在官网下载jdk1.7、maven3.2.1、ant1.9.4,解压设置好环境变量就可以用。
环境变量设置如下:
(1)执行vim /etc/profile
(2)在文件尾部加入:
export JAVA_HOME=/home/spark/jdk1.7
export MAVEN_HOME=/ho
- StatusBar 字体白色
pangyulei
status
[[UIApplication sharedApplication] setStatusBarStyle:UIStatusBarStyleLightContent];
/*you'll also need to set UIViewControllerBasedStatusBarAppearance to NO in the plist file if you use this method
- 如何分析Java虚拟机死锁
sesame
javathreadoracle虚拟机jdbc
英文资料:
Thread Dump and Concurrency Locks
Thread dumps are very useful for diagnosing synchronization related problems such as deadlocks on object monitors. Ctrl-\ on Solaris/Linux or Ctrl-B
- 位运算简介及实用技巧(一):基础篇
tw_wangzhengquan
位运算
http://www.matrix67.com/blog/archives/263
去年年底写的关于位运算的日志是这个Blog里少数大受欢迎的文章之一,很多人都希望我能不断完善那篇文章。后来我看到了不少其它的资料,学习到了更多关于位运算的知识,有了重新整理位运算技巧的想法。从今天起我就开始写这一系列位运算讲解文章,与其说是原来那篇文章的follow-up,不如说是一个r
- jsearch的索引文件结构
yangshangchuan
搜索引擎jsearch全文检索信息检索word分词
jsearch是一个高性能的全文检索工具包,基于倒排索引,基于java8,类似于lucene,但更轻量级。
jsearch的索引文件结构定义如下:
1、一个词的索引由=分割的三部分组成: 第一部分是词 第二部分是这个词在多少